БГРсз-18-12 РГР №2. Решение в программе
 Скачать 37.3 Kb. Скачать 37.3 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Филиал в г. Октябрьском Кафедра «Разведка и разработка нефтяных и газовых месторождений» РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2 по дисциплине «Математические методы обработки результатов экспериментов» Студент группы БГРсЗ-18-12 Старший преподаватель Ф. К. Усманова Октябрьский 2021 Расчетно-графическая работа № 2 Задание: Получить эмпирическую формулу линейной регрессии, решая систему уравнений (можно с помощью встроенных функций Excel и MathCAD). Оценить тесноту связи. Решение в программе Excel По заданным парам значений
рассчитать параметры линейной функции y=a+bx. Оценить тесноту связи. Р е ш е н и е Для расчета параметров a, bлинейной регрессии y=a+bxсначалаоформимвспомогательную таблицу, затемпо полученным результатам (см. последнюю восьмую строку таблицы) составим систему линейных уравнений вида: 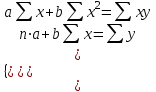 В таблице по исходным данным рассчитаны значения для 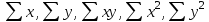 . .
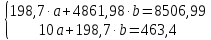 Решая полученную систему уравнений одним из известных способов, имеем: a=61,57,b=-0,76. Значит, уравнение регрессии имеет вид: y=61,57-0.76x. Чтобы оценить тесноту связи, рассчитаем коэффициент детерминации 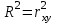 , где , где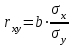 - линейный коэффициент парной корреляции; - линейный коэффициент парной корреляции;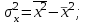 σх - среднее квадратическое отклонение x; σх - среднее квадратическое отклонение x;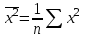 - среднее квадратов значений x; - среднее квадратов значений x;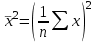 - квадрат среднего значения x; - квадрат среднего значения x;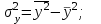 σу- среднее квадратическое отклонение y; σу- среднее квадратическое отклонение y; - среднее квадратов значений y; - среднее квадратов значений y;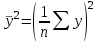 - квадрат среднего значения y. - квадрат среднего значения y.В нашем случае получим: ͞x = 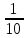 ∙ 198,7 = 19,87 ; ͞ ∙ 198,7 = 19,87 ; ͞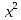 = = 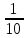 ∙ 4861,98 = 486,198; ∙ 4861,98 = 486,198;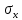 = =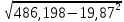 = 9,56 = 9,56͞y = 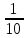 ∙ 463,4 = 46,34 ; ͞ ∙ 463,4 = 46,34 ; ͞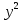 = = 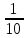 ∙ 24334,34 = 2433,434 ∙ 24334,34 = 2433,434Аналогично получаем σу = 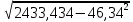 = 16,9 = 16,9Тогда 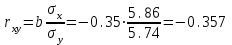 ; ; 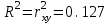 . .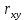 = b = b 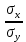 = - 0,76 ∙ = - 0,76 ∙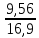 = -0,43 ; = -0,43 ; 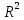 = = 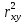 = 0,185 = 0,185Таким образом, лишь 18,5 % изменения результата yобъясняется изменением фактора x. Вопросы при защите РГР №2 Что такое регрессионный анализ? Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. В чем смысл метода наименьших квадратов (МНК)? Смысл метода наименьших квадратов заключается в том, что отыскиваются такие значения коэффициентов уравнения регрессии, при которых сумма квадратов отклонений фактических значений варьирующего признака от вычисленного по уравнению была бы наименьшей из всех возможных Какой вид у системы уравнений для уравнения у=ах + в? Линейное уравнение с двумя переменными Каким образом может быть использована программа Exсel? С её помощью можно получить решение уравнения линейной регрессии, определить коэффициент детерминации для того, чтобы оценить тесноту связи. Что понимают под значимостью коэффициента регрессии? Проверка статистической значимости коэффициентов линейной регрессии заключается в проверке гипотезы значимости или незначимости отличия оценок некоторых регрессионных коэффициентов от нуля. Если в результате проверки оказывается, что отличие оценок каких-то регрессионных коэффициентов от нуля не влияет на качество модели, то соответствующие предикторные переменные можно исключить из регрессионной модели. |
