Решение в событие обрыва для каждой из схем а 1 2 3 4
 Скачать 35.44 Kb.
|
|
Вариант 11 Задача 1. Задана электрическая схема системы, состоящей из четырех элементов. Событие - отказ 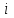 - го элемента за некоторый промежуток времени. Вероятности отказов элементов заданы: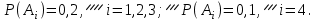 Найти вероятность обрыва для каждой из схем. Решение: В – событие обрыва для каждой из схем. а) 1 2 3 4 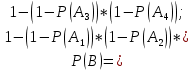 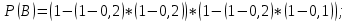 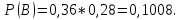 б) 2 1 3 4 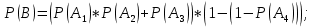 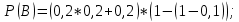 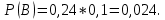 Ответ: а) 0,1008; б) 0,024. Задача 2. Отдельные символы двоичного сообщения могут быть искажены из-за воздействия импульсных ошибок с вероятностью р от корректности передачи других символов. Код исправляет не более 2 ошибок в сообщении. Передано сообщение из n информационных символов. Какова вероятность, что оно не сможет быть корректно декодировано? Решение: B – событие, что сообщение не сможет быть декодировано, то есть будет более 2 ошибок. Используем вероятность противоположного события. 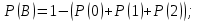 Используем формулу Бернулли: 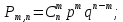 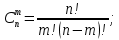 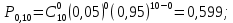 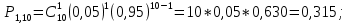 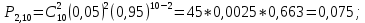 Искомая вероятность 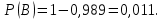 Ответ: 0,011. Задача 3. Дан закон распределения дискретной случайной величины. Вычислить дисперсию и построить функцию распределения. Решение:
Математическое ожидание находим по формуле m = ∑xipi = 0,4; 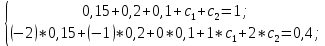 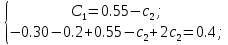 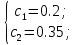 Дисперсию находим по формуле D = ∑x2ipi - M[x]2. Дисперсия D[X]. 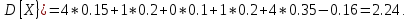 Функция распределения: 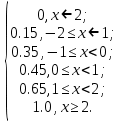 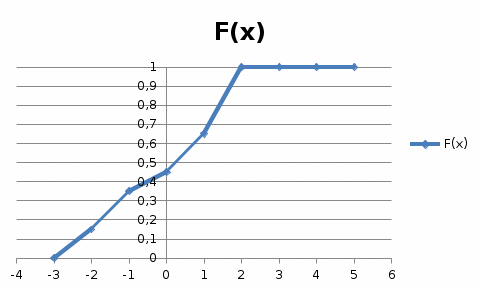 Задача 4. Дана плотность распределения непрерывной случайной величины. Найти функцию распределения, построить ее график, вероятность попадания в заданный интервал, математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение: 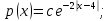 Для нахождения функции распределения проинтегрируем плотность распределения: 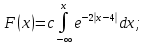 Рассмотрим 2 случая: 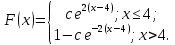 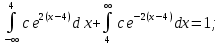 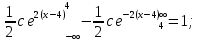 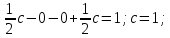 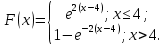 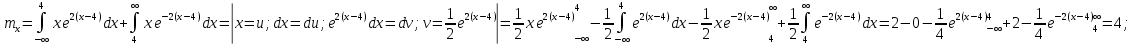 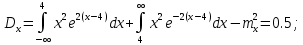 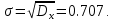 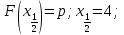 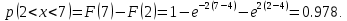 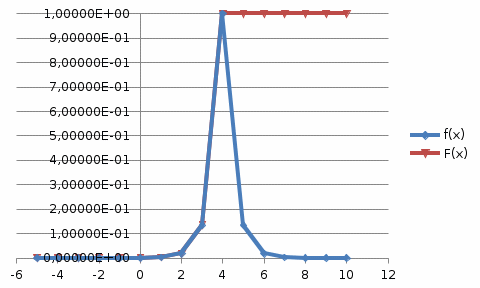 |