Шпаркалка меирология хулония. Решение В16, Р90%, дефект А
 Скачать 15.47 Kb. Скачать 15.47 Kb.
|
|
Семинар 2 Вариант 19 Шипаев Задача 1. Трубным заводом выпущена пробная партия труб в количестве 1000 шт. При выборочной проверке 100 изделий были обнаружены дефекты 3-х видов. В каких пределах находится число дефектов определенного вида во всей партии с вероятностью Р (табл. 11.3)? Решение В=16, Р=90%, дефект А В первую очередь задаёмся доверительной вероятностью. С учётом небольших финансовых потерь за счёт этих дефектов, выбираем P = 0,99. Тогда t = 1,984. Используя формулы (4.1.1) и (4.1.2), для дефектов вида А находим: 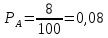 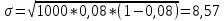 Теперь по формуле (4.1.4) находим границы 90 % доверительного интервала: 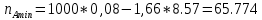 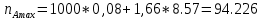 Итак, в партии из 1000 изделий ожидаемое (наиболее вероятное) число дефектов составляет 110, при этом с вероятностью 90 % можно обнаружить от 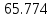 до до 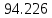 дефектов вида А. дефектов вида А. Задача 2. Те же 100 труб из предыдущей задачи разделены на партии по 100 штук, направляемые в разные адреса. В каких пределах будет находиться число дефектов в этих партиях (табл. 11.3)? Решение На этот раз следует воспользоваться формулой (4.1.3), которая характеризует рассеяние частостей, полученных по выборкам объёма N: 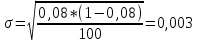 Учитывая, что вероятное значение p составляет 0,11, находим предельные значения доверительного интервала (при P = 0,90): 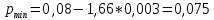 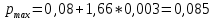 Поэтому количество дефектов вида А в разных партиях будет находиться в пределах: nAmin = 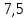 : nAmax = : nAmax = 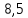 . . |
