Найти частные производные первого порядка для функции z = f(x, y).

Найти частные производные второго порядка для функции z = f(x, y) и показать, что она удовлетворяет данному уравнению.

Проверяем уравнение:
 Решение верное. Решение верное.
Даны функция  и точки А(4,1) и В(3,98;1,06). Требуется: и точки А(4,1) и В(3,98;1,06). Требуется:
Вычислить точное значение в точке В;
вычислить приближенно значение функции в точке В, исходя из значения функции в токе А, и заменив приращение функции при переходе от токи А к точке В дифференциалом;
оценить относительную погрешность вычислений в процентах;
Составить уравнение касательной плоскости и нормали к поверхности  в точке С(4,1,z0). в точке С(4,1,z0).

Будем рассматривать z(В) как частное значение функции  при x = 3,98 = x1, у =1,06 = у1. За x0 принимаем число 4, за у0 –число 1. при x = 3,98 = x1, у =1,06 = у1. За x0 принимаем число 4, за у0 –число 1.
Тогда z(x0,y0) =  ; ;
dx = x1 – x0 =3,98-4=-0,02,
dy = y1 –y0 =1,06-1=0,06
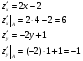
Тогда получим:
 z(x0,y0) + z(x0,y0) +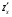 (x0,y0)dx+ (x0,y0)dx+ (x0,y0)dy=8+6*(-0.02)-1*0.06=7,82 (x0,y0)dy=8+6*(-0.02)-1*0.06=7,82
Оценим погрешность:  или 0,04% или 0,04%
Если поверхность задана уравнением  , то уравнение касательной плоскости к данной поверхности в точке , то уравнение касательной плоскости к данной поверхности в точке  можно найти по следующей формуле: можно найти по следующей формуле:
z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)

 – общее уравнение касательной плоскости. – общее уравнение касательной плоскости.
Составим канонические уравнениянормали по точке 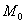 и направляющему вектору и направляющему вектору 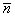 : :

 – уравнение нормали. – уравнение нормали.
Найти наибольшее и наименьшее значение функции в замкнутой области D. Сделать чертеж.
 ; ;
Д: 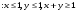 ; ;

Найдём стационарные точки внутри области D.
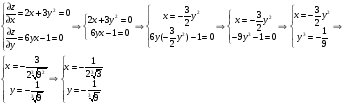 Получили точку С ( Получили точку С ( , ,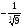 ) вне области D. ) вне области D.
Найдём наибольшее и наименьшее значение функции на линиях, образующих границу области.
А) на линии у=1
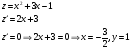
 не принадлежит области. не принадлежит области.
Б) на линии у=1-х
 
Решения нет.
в) на линии х=1


Найдем значения в угловых точках 
Наибольшее значение находится в точке (1,1) и равно 3, наименьшее в точке (0,1) и равное -1.
Исследовать функцию  на экстремум при условии на экстремум при условии  . .
Составляем функцию Лагранжа:

Имеем следующие решения:  , ,
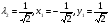
Рассмотрим достаточное условие экстремума, для этого найдём производные второго порядка.

При   , значит, в этой точке условный максимум , значит, в этой точке условный максимум 
При 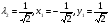 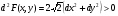 , значит, в этой точке условный минимум , значит, в этой точке условный минимум 
Дана функция  , точка , точка  и вектор и вектор 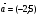 . Найти grad(z) в точке А и производную функции z в точке А по направлению вектора а. . Найти grad(z) в точке А и производную функции z в точке А по направлению вектора а.
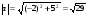
Тогда единичный направляющий вектор:

Градиент равен 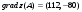 . .
Теперь находим производную по направлению:

Экспериментально получены пять значений искомой функции  при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида  , выражающую приближенно функцию , выражающую приближенно функцию  . Сделать чертеж, на котором в декартовой системе координат построить экспериментальные точки и график аппроксимирующей функции . Сделать чертеж, на котором в декартовой системе координат построить экспериментальные точки и график аппроксимирующей функции 
x
|
1
|
2
|
3
|
4
|
5
|
y
|
5,2
|
6,2
|
4,7
|
2,7
|
3,2
|
Применяя метод наименьших квадратов, найдём неизвестные параметры а и b.
х
|
у
|
Х2
|
ху
|
1
|
5,2
|
1
|
5,2
|
2
|
6,2
|
4
|
12,4
|
3
|
4,7
|
9
|
14,1
|
4
|
2,7
|
16
|
10,8
|
5
|
3,2
|
25
|
16
|
 15 15
|
 22 22
|
 55 55
|
 58,5 58,5
|
Составляем систему уравнений:

Т.о. Y=-0,72X+6.65.
Построим график функции:

Вычислить двойной интеграл
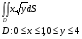

 |
 Скачать 118.88 Kb.
Скачать 118.88 Kb.

 Решение верное.
Решение верное. ;
;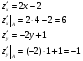
 z(x0,y0) +
z(x0,y0) +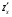 (x0,y0)dx+
(x0,y0)dx+ (x0,y0)dy=8+6*(-0.02)-1*0.06=7,82
(x0,y0)dy=8+6*(-0.02)-1*0.06=7,82
 – общее уравнение касательной плоскости.
– общее уравнение касательной плоскости.
 – уравнение нормали.
– уравнение нормали. ;
; 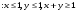 ;
; 
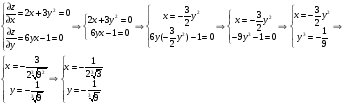 Получили точку С (
Получили точку С ( ,
,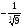 ) вне области D.
) вне области D.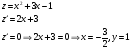
 не принадлежит области.
не принадлежит области.





 ,
, 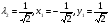


 , значит, в этой точке условный максимум
, значит, в этой точке условный максимум 
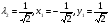
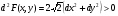 , значит, в этой точке условный минимум
, значит, в этой точке условный минимум 
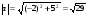

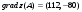 .
.


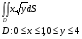



 и точки А(4,1) и В(3,98;1,06). Требуется:
и точки А(4,1) и В(3,98;1,06). Требуется: в точке С(4,1,z0).
в точке С(4,1,z0).
 или 0,04%
или 0,04% , то уравнение касательной плоскости к данной поверхности в точке
, то уравнение касательной плоскости к данной поверхности в точке  на экстремум при условии
на экстремум при условии  .
. , точка
, точка  и вектор
и вектор 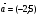 . Найти grad(z) в точке А и производную функции z в точке А по направлению вектора а.
. Найти grad(z) в точке А и производную функции z в точке А по направлению вектора а. при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида
при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию вида  , выражающую приближенно функцию
, выражающую приближенно функцию 
 15
15