МЖГ. Решение Выберем сечения 11 и 22 проходящие по месту присоединения манометра 1 и 2 соответственно
 Скачать 118.2 Kb. Скачать 118.2 Kb.
|
|
Задача 5 – Расчет трубопровода. Вариант - 11 По магистральному трубопроводу жидкость “Ж” поступает в накопительный резервуар, из которого осуществляется ее раздача потребителям. Накопительный резервуар имеет достаточный объем и снабжен клапаном регулировки давления, обеспечивающим функционирование системы в диапазоне давлений onPmin до Pmax. В данный момент времени все потребители кроме одного отключены. Показания манометров фиксируют давления P1 на входе в магистральный трубопровод и давление P2 при подаче жидкости потребителю. Длина магистрального трубопровода от манометра 1 до накопительного резервуара – L1, диаметр – D1. Трубопровод изготовлен из материала M1. Подающий трубопровод имеет длину от накопительного резервуара до манометра 2 – L2, диаметр – D2, материал – M2. В подающем и приемном трубопроводах имеются местные сопротивления. 1. Определить массовый расход жидкости. 2. В некоторый момент времени в накопительном резервуаре происходит авария, в результате которой возникает течь площадью Sa. Определить величину утечки жидкости (кг/сек). Коэффициент расхода утечки принять равным 0.6. Дано: дизтопливо; Р1=12 МПа=12*106Па; L1=200м; D1=150 мм=0,15м; М1=стальные сварные умеренно заржавевшие; Р2=8МПа=8*106Па; L2=50м; D2=50мм=0,05м; М2=бесшовные стальные после нескольких лет; Sа=3 мм2=3*10-6м2; μ=0,6. 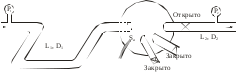 Рисунок 1 – Конфигурация трубопроводной системы и местные сопротивления Решение 1. Выберем сечения 1-1 и 2-2 проходящие по месту присоединения манометра 1 и 2 соответственно. 2. Составим уравнение Бернулли для сечений 1-1 и 2-2 : 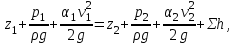 (1) (1)где z1, z2 – геометрический напор в сечении 1-1 и 2-2, м; р1, р2 –избыточное давление жидкости в сечении 1-1 и 2-2, Па; v1, v2 - средняя скорость потока в сечении 1-1 и 2-2, м/с; α1, α2- коэффициент Кориолиса в сечении 1-1 и 2-2; ρ – плотность жидкости, кг/м3; Σh – суммарные потери напора между сечениями 1-1 и 2-2. Геометрическая высота в сечениях одинакова z1 = z2=0. Давления в сечениях: р1=12*106Па ; р2 =8*106Па. Плотность дизтоплива ρ =840кг/м3. Примем коэффициенты Кориолиса для сечений как для турбулентного течения α1= α2 =1. С учетом известных величин уравнение (1) примет вид 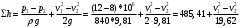 (2) (2)2. Суммарные потери напора 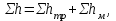 (3) (3)где Σhтр - суммарные потери напора на трение; Σhм - суммарные местные потери напора. 3. Суммарные потери напора на трение 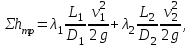 (4) (4)где L1, L2 – длины соответственно магистрального и подающего трубопровода, м; D1, D2 – диаметр соответственно магистрального и подающего трубопровода, м; λ1, λ2 – коэффициент гидравлического сопротивления трения соответственно магистрального и подающего трубопровода, м 4. Суммарные местные потери напора 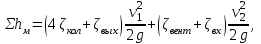 (5) (5)где 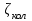 =0,23– коэффициент местного сопротивления плавного колена 900; =0,23– коэффициент местного сопротивления плавного колена 900;  = 1,0– коэффициент местного сопротивления выхода из трубы; = 1,0– коэффициент местного сопротивления выхода из трубы;  = 0,5– коэффициент местного сопротивления входа в трубу с острыми кромками; = 0,5– коэффициент местного сопротивления входа в трубу с острыми кромками; 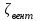 =4,0 – коэффициент местного сопротивления вентиля =4,0 – коэффициент местного сопротивления вентиля 5. С учетом формул (3) -(5) уравнение (2) принимает вид 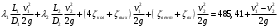 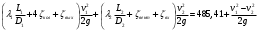 (6) (6)6. Расход через трубопровод согласно уравнению неразрывности потока  (7) (7)где Q – расход через трубопровод; ω1 – площадь трубы в сечении 1-1; ω2 – площадь трубы в сечении 2-2 Выразим из (7) скорость в магистральном трубопроводе v1через скорость в подающем v2 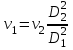 (8) (8)7. Подставляем выражение (8) в уравнение (6) и находим скорость v2 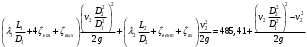 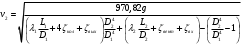 (9) (9)8. Скорость течения найдем методом последовательных приближений. 8.1 Первое приближение Считаем течение в трубопроводе турбулентным. В качестве первого приближения принимаем квадратичную область сопротивления и определяем коэффициент гидравлического сопротивления трения для каждого участка по формуле Шифринсона 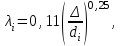 (10) (10)где Δ-эквивалентная шероховатость труб. В магистральном трубопроводе из стальных сварных трубумеренно заржавевшихΔ1= 0,5 мм; в подающем трубопроводе из бесшовные стальные после нескольких лет.Δ2= 0,2мм 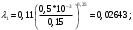 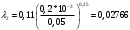 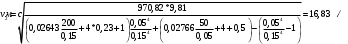 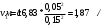 8.2 Второе приближение Определяем число Рейнольдса на каждом участке 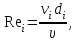 (11) (11)где υ=0,055см2/с=0,055*10-4 м2/с - кинематическая вязкость дизтоплива 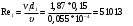 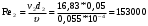 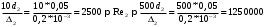 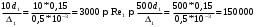 Критерий Рейнольдса находится в области доквадратичного сопротивления. λiпересчитываем по формуле Альтшуля:  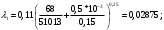 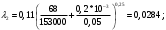 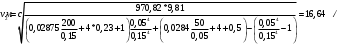 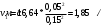 9. Определяем объемный расход через трубопровод по (7) 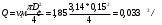 10. Определяем массовый расход через трубопровод  (12) (12)11. Определим рабочий напор в резервуаре  (13) (13) 12. Расход утечки через отверстие:  (14) (14)где μ – коэффициент расхода отверстия; Sа – площадь отверстия Принимаем коэффициент расхода отверстия μ =0,60. 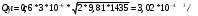 13. Определяем массовый расход утечки 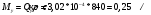 (15) (15) |
