математика. Математика. Решение Вычислим интеграл, используя формулу Уравнение прямой имеет вид Вычислим интеграл
 Скачать 196 Kb. Скачать 196 Kb.
|
|
Криволинейный интеграл 1 рода Вариант 1 Вычислите криволинейный интеграл 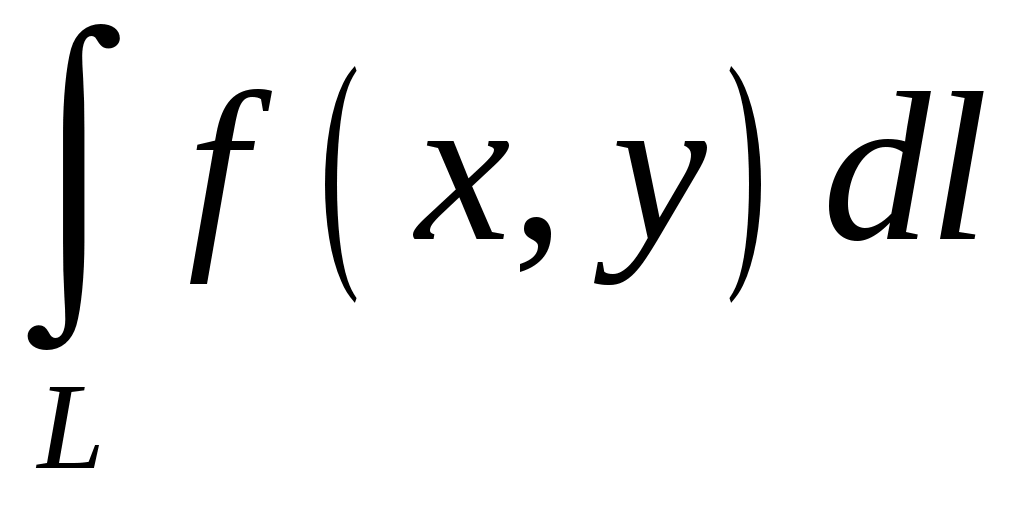 , где , где 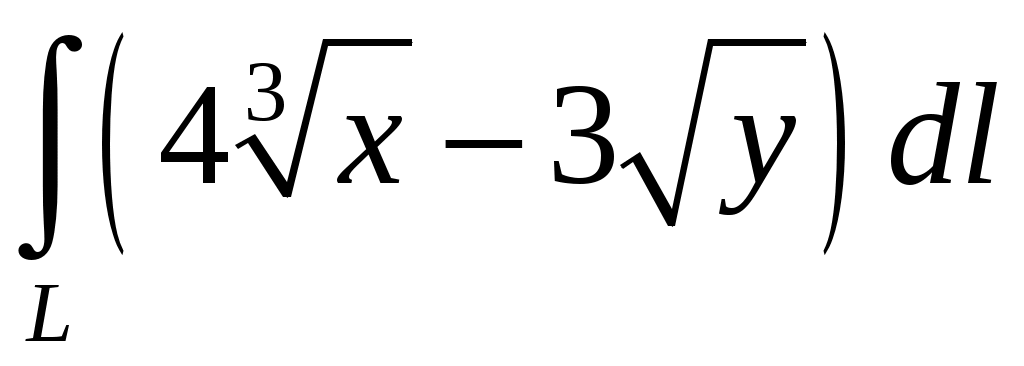 , , Решение: Вычислим интеграл, используя формулу: Уравнение прямой  . .Вычислим интеграл:  Задания по задачнику Кузнецова Вариант 1 4. Исследовать на сходимость ряд. Решение: Применим признак Даламбера. Вычислим предел.  Предел конечен и меньше единицы, следовательно, ряд сходится. 5. Исследовать на сходимость ряд. Решение: Применим радикальный признак Коши. Вычислим предел.  Предел конечен и меньше единицы, следовательно, ряд сходится. 7. Исследовать на сходимость ряд. Решение: Применим признак Лейбница. 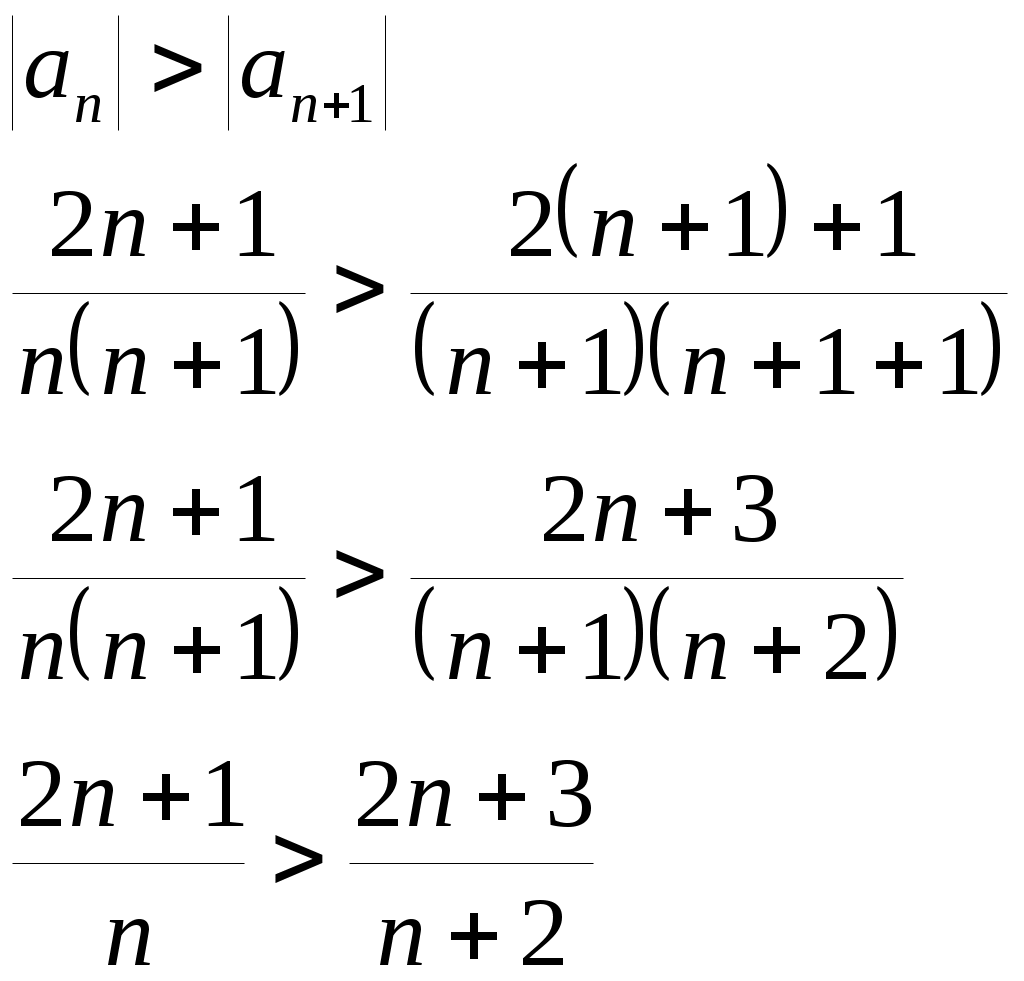  Следовательно, первое условие признака Лейбница 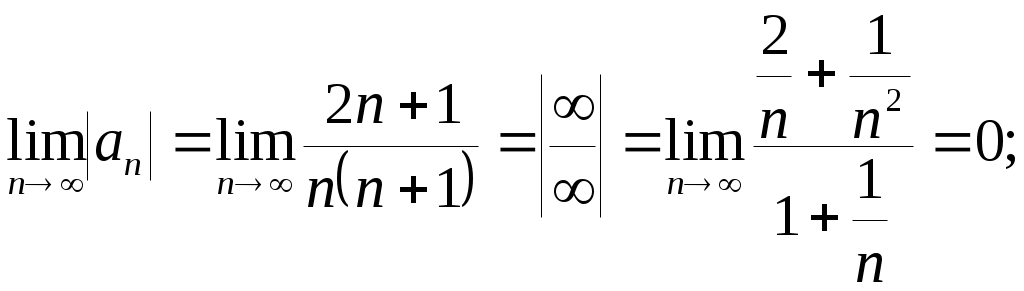 Т.е. второе условие признака Лейбница выполнено, следовательно, ряд сходится. Исследуем на сходимость ряд 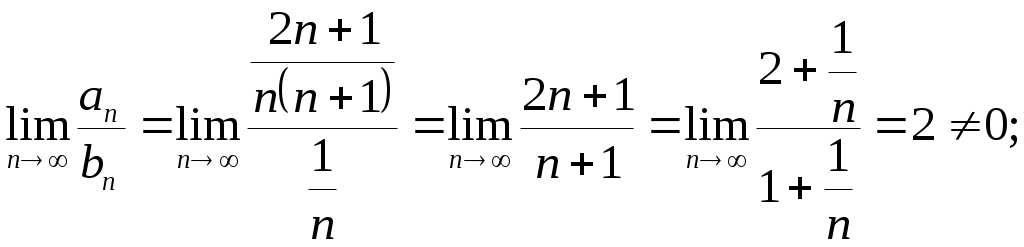 Предел конечен и не равен нулю, следовательно, ряд 10. Найти область сходимости ряда. Решение: Найдем радиус сходимости, используя признак Даламбера. 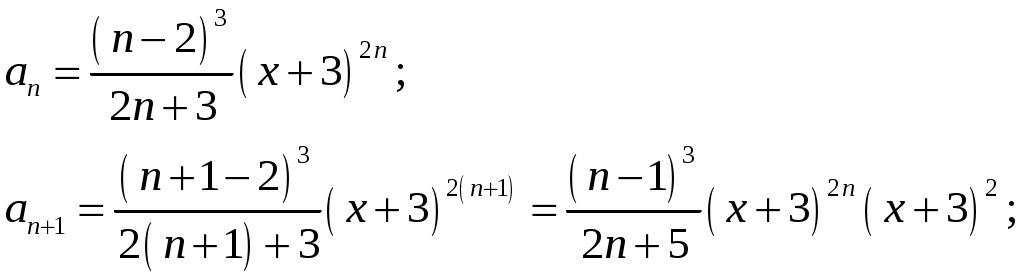 Вычислим предел:  Чтобы ряд сходился, необходимо, чтобы: Исследуем сходимость на конце интервала. При 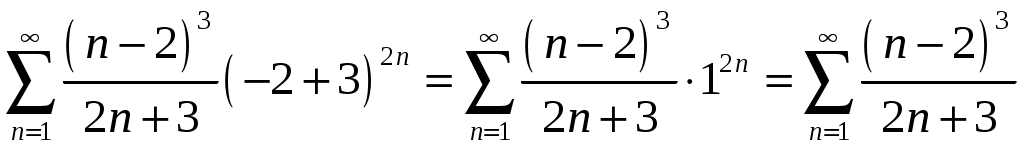 . . Применим необходимый признак. 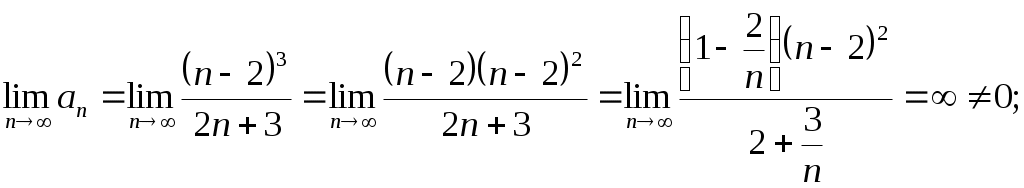 Необходимый признак не выполняется, следовательно, ряд При 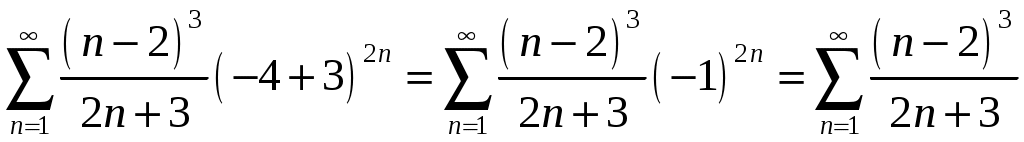 . . Ряд расходится, следовательно, граница 14. Разложить функцию в ряд Тейлора по степеням Решение: Разложим знаменатель на множители:  Разложим дробь откуда При при тогда В разложении 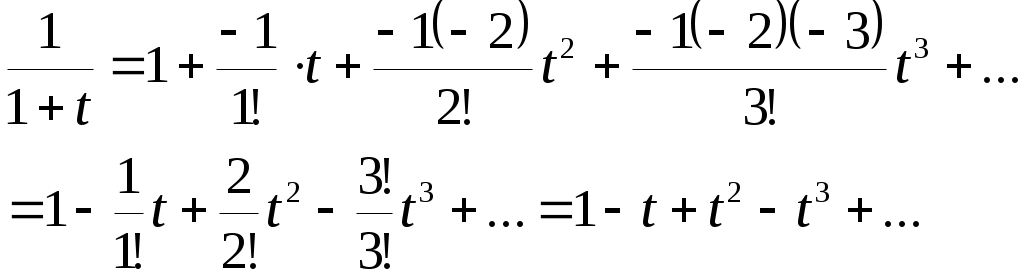 Разложим дроби  в ряд: в ряд: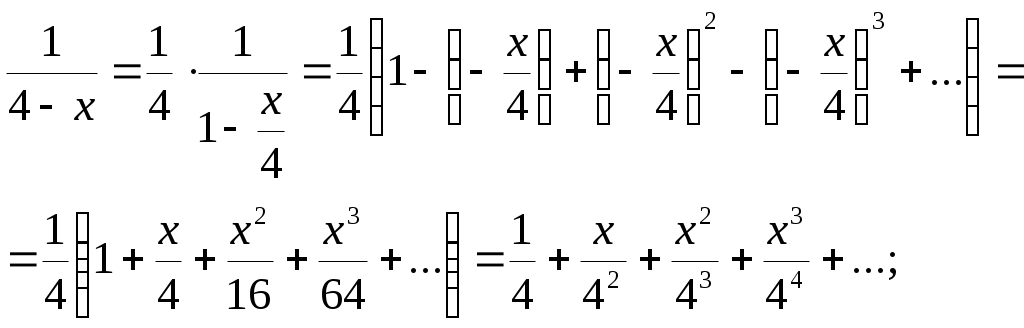  Окончательно получим: 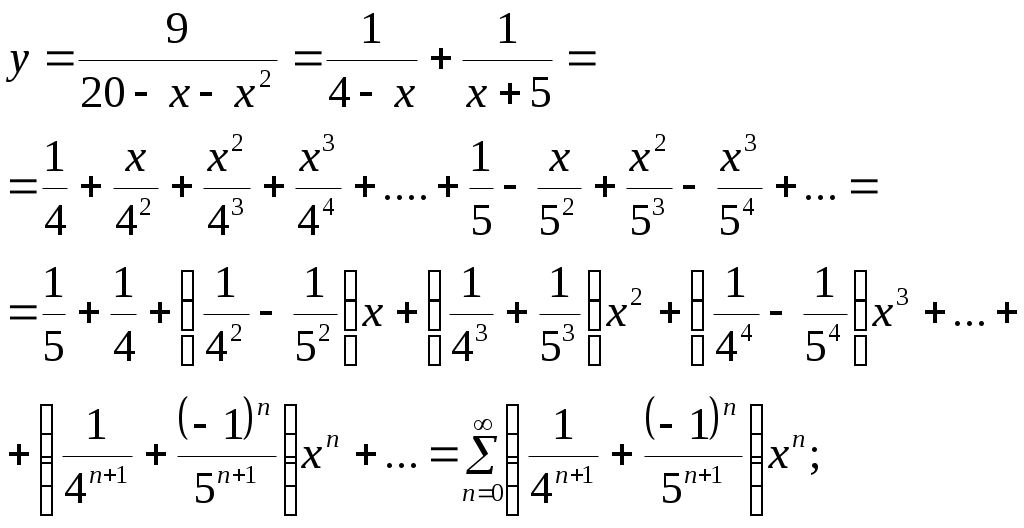 Так как ряд сходится для  Откуда 15. Вычислить интеграл с точностью до 0,001. Решение: В разложении 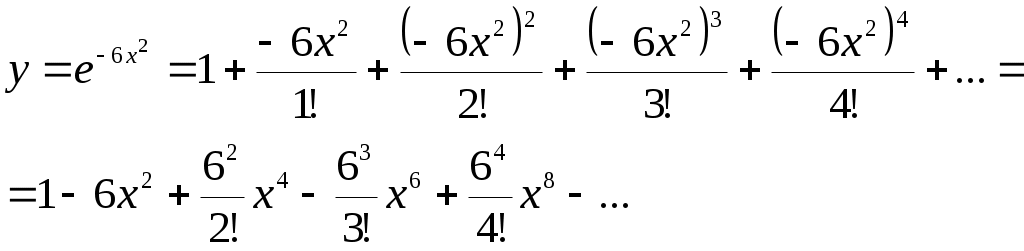 Подставив в интеграл, получим:   Члены знакочередующегося ряда, начиная с 3-го, меньше 0,001, значит, их можно отбросить. При этом погрешность вычислений меньше первого отброшенного члена ряда. |
