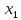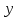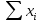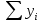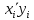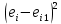Решение Выполнить центрирование факторов
 Скачать 24.84 Kb. Скачать 24.84 Kb.
|
|
Задание №5 Многофакторный регрессионный анализ На основе заданного массива данных построить уравнение регрессии в виде линейного алгебраического полинома от двух переменных, проверить его адекватность и значимость факторов. Расчёты произвести в матричной форме. Порядок выполнения задания. 1. Выполнить центрирование факторов 2. Составить матричное уравнение с вектором неизвестных оценок коэффициентов регрессии. 3. Найти решение матричного уравнения - оценки коэффициентов регрессии. 4. Проверить адекватность построенного уравнения регрессии экспериментальным данным по критерию Фишера при уровне значимости α = 0,05. 5. Выполнить селекцию факторов по критерию Стьюдента при таком же уровне значимости. 6. Повторно проверить адекватность уравнения регрессии после исключения незначимых факторов. Таблица 1. Исходные данные
Решение Выполнить центрирование факторов Факторы считаются центрированными, если 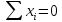 . Если данное условие не выполняется, то необходимо сдвинуть центр. Для этого из каждого значения необходимо вычесть их среднее арифметическое . Если данное условие не выполняется, то необходимо сдвинуть центр. Для этого из каждого значения необходимо вычесть их среднее арифметическое 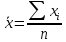 . .Рассчитаем среднее арифметическое для каждого фактора. Таблица 2. Среднее арифметическое
Таблица 3. Центрированные факторы
2. Составить матричное уравнение с вектором неизвестных оценок коэффициентов регрессии. Уравнение множественной регрессии представляет собой зависимость объясняемой переменной Y от нескольких объясняющих переменных X: 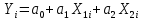 Систему можно записать в матричном виде: 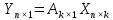 3. Найти решение матричного уравнения - оценки коэффициентов регрессии. Согласно методу наименьших квадратов, вектор A получается из выражения: 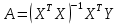 К матрице с переменными Xj добавляем единичный столбец:
Матрица Y
Находим транспонированную матрицу 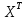
Умножаем матрицы 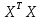
Умножаем матрицы 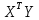
Находим обратную матрицу 
Вектор оценок коэффициентов регрессии равен
Уравнение регрессии (оценка уравнения регрессии) 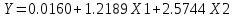 4. Проверить адекватность построенного уравнения регрессии экспериментальным данным по критерию Фишера при уровне значимости α = 0,05. Матрица A, составленная из Y и X:
Транспонированная матрица.
Матрица 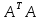 . .
Полученная матрица имеет следующее соответствие:
Найдем парные коэффициенты корреляции. 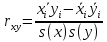 Матрица коэффициентов корреляции:
Найдем 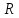 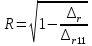 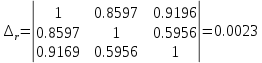 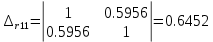 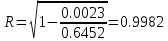 Отсюда 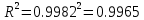 Критерий Фишера рассчитаем по формуле: 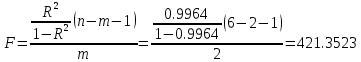 Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 6 - 2 - 1 = 3: 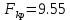 Поскольку фактическое значение F > 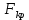 , то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно. , то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно.5. Выполнить селекцию факторов по критерию Стьюдента при таком же уровне значимости. Для несмещенной оценки дисперсии проделаем следующие вычисления:
Оценка дисперсии равна:  Несмещенная оценка дисперсии равна:  Оценка среднеквадратичного отклонения:  Найдем оценку ковариационной матрицы вектора 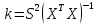
Дисперсии параметров модели определяются соотношением 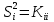 , т.е. это элементы, лежащие на главной диагонали: , т.е. это элементы, лежащие на главной диагонали: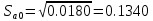 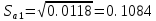 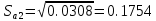 Значимость коэффициентов регрессии: 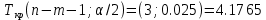 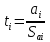 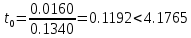 Статистическая значимость коэффициента регрессии 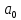 не подтверждается. не подтверждается.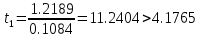 Статистическая значимость коэффициента регрессии 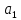 подтверждается. подтверждается.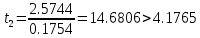 Статистическая значимость коэффициента регрессии 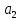 подтверждается. подтверждается.Коэффициенты уравнения регрессии значимы, факторы из модели не исключаются. 6. Повторно проверить адекватность уравнения регрессии после исключения незначимых факторов. Не требуется, так как факторы из модели не исключались. |