Задачи по физике 1 курс. Задачи по физике. Решение Вначале найдем время, за которое капля дождя достигает земли с края зонта
 Скачать 151.52 Kb. Скачать 151.52 Kb.
|
|
Задача 1 С башни, высотой 35 м, в горизонтальном направлении со скоростью 11 м/с брошен камень. Чему равна его скорость в момент падения? Решение: Движение камня, брошенного горизонтально, представляет собой комбинацию двух движений, взаимно перпендикулярных друг другу: - равномерное движение по горизонтали, - равноускоренное по вертикали В результате траектория падения камня имеет вид параболы.  Скорость камня в любой момент времени будет равна векторной сумме горизонтальной и вертикальной составляющей скорости. Угол между векторами этих скоростей всегда прямой, следовательно, для определения скорости в момент падения камня, брошенного горизонтально, применим теорему Пифагора. Скорость камня будет равна корню квадратному из суммы квадратов горизонтальной и вертикальной составляющих в данный момент времени v=√(vгор²+ vверт²). vгор = 11 м/с, vверт = √2*g*h, где g – ускорение свободного падения (9,81 м/с2), h – высота падения камня (h = 35 м) v = √121 + (2*9,81*35) ≈ 28,42 м/с Ответ: скорость камня в момент падения равна 28,42 м/с Задача 2 С какой наибольшей скоростью должен идти под дождем человек, чтобы дождь не попадал на ноги, если он держит зонт на высоте 157 см над землей так, что край его выступает вперед на 22 см? Капли дождя падают вертикально со скоростью 12 м/с. Решение: Вначале найдем время, за которое капля дождя достигает земли с края зонта. t = h / v = 1,57 / 12 ≈ 0,13 с (расстояние, которое преодолевает капля до земли разделим на скорость капли) Теперь найдем скорость, с которой должен идти человек vчеловека = s / t, где s – край зонта vчеловека = 0,22 / 0,13 ≈ 1,69 м/с = 6,084 км/ч Ответ: человек должен идти со скоростью 6 км/ч Задача 3 Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, меньше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 80 с вектором ее линейной скорости. Решение:            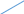 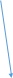    α=80 v a at an  an – нормальное ускорение (всегда направлено к центру) at – тангенциальное (касательное) ускорение (направлено по касательной к окружности) a – полное ускорение v – линейная скорость  A  C  B Нам необходимо найти отношение at к an Рассмотрим треугольник ABC. В нем сторона BC равна an, т.к. an перпендикулярно at. Тогда an = a * sin α, at = a * cos α at / an = a * cos α / a * sin α = cos α / sin α = ctg α = ctg 8 = 7,1154 Мы получили, что тангенциальное ускорение больше нормального в 7,1154 раз. Следовательно, нормальное ускорение меньше тангенциального в те же 7,1154 раза. Ответ: 7,1154 Задача 4 Через сколько секунд вектор скорости тела, брошенного под углом 450 к горизонту с начальной скоростью 19 м/с, будет составлять с горизонтом угол 150? Решение:  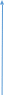 Y            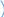       β=150 Vy1 Vx1 Vx0 Vy0 α=450 V0 X Горизонтальная составляющая скорости постоянная: Vx0 = Vx1 Разница вертикальной составляющей скорости тела: Ϫ = g * t, где g – ускорение свободного падения (9,81 м/с2), t – искомое время. Отсюда находим время: t = Ϫ / g Ϫ = Vy0 - Vy1 Vy0 = Vx0, т.к. тело брошено под углом 450. Vy0 = Vx0 = V0 * cos α Vy1 = Vx1 * tg β t = V0 * cos α - Vx1 * tg β / g = V0 * cos α - V0 * cos α * tg β / g = V0 * cos α (1- tg β) / g = 19 * cos 45 (1 – tg 15) / 9,81 = 19 * 0,7 (1 – 0,268) / 9,81 ≈ 0,99 = 1 с Ответ: через 1 секунду Задача 5 Определить начальную скорость камня, брошенного под углом к горизонту, если известно, что наибольшая высота подъема равна 15м, а радиус кривизны траектории в ее верхней точке равен 45м. Решение:  Y     V     g=9,81м/с2    Vyв=0 Vxв Vy      h=15м   Vx X  r=45м Vy = √2*g*h, где g – ускорение свободного падения (9,81 м/с2) Vyв – вертикальная составляющая скорости камня в верхней точке равна нулю Vyв = 0 Vxв – горизонтальная составляющая скорости камня в верхней точке равна Vx Vx = Vxв = √R*g V = √ Vy2 + Vx2 Vy = √2*9,81*15 = 17,155 м/с Vx = √45*9,81 = 21,011 м/с V = √17,1552 + 21,0112 = 27,12 м/с Ответ: начальная скорость камня 27,12 м/с Задача 6 При выстреле из пистолета в горизонтальном направлении пуля летела 2 с до первого из двух вертикально закрепленных листов бумаги, расстояние между которыми 1 м. Определить скорость пули, если пробоина во втором листе на 5 см ниже, чем в первом. Решение:              g=9,81м/с2 Vx Vx    Vy Vy1 h=0,05м      Vy2 Vx   t = 2 с s = 1 м  t1 Vy = 0 В полете на пулю действует только сила тяжести, придающая ей вертикальное ускорение, равное g. Таким образом подлетев к первому листу бумаги пуля уже имела и вертикальную составляющую скорости: Vy1 = g * t t1 = s / Vx, где t1 – время, за которое пролетела пуля между листами, s – расстояние между листами. Подлетев ко второму листу бумаги, пуля имела вторую вертикальную составляющую скорости: Vy2 = √Vy12 + 2*g*h Разница между двумя вертикальными составляющими скорости: Ϫ = Vy2 - Vy1 Т.к. пуля летит равноускоренно по Y, то изменение скорости равно: Vy2 - Vy1 = g * t1 (√ (g * t)2 + 2*g*h) - g * t = g * t1 (√ g2 * t2 + 2*g*h) - g * t = g * s / Vx Находим скорость пули: Vx = g * s / (√ g2 * t2 + 2*g*h) - g * t = 9,81*1 / (√9,812*22+2*9,81*0,05)-9,81*2 = 9,81 / 0,02498 ≈ 392 м/с Ответ: скорость пули равна 392 м/с Задача 7 Точка движется по окружности радиусом 56 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 4 с после начала движения, если к концу пятого оборота после начала движения линейная скорость точки стала равной 3 м/с. Решение:     an     N = 5 об, t = 4 с   at  R = 0,56 м  v = 3 м/с Нормальное ускорение точки an = ω2 * R, где ω – угловая скорость ω = β * t, где β – угловое ускорение Подставляем в первую формулу и получаем: an = β2 * t 2 * R При равноускоренном движении среднее число оборотов в единицу времени: nср = N / t1, где t1 – момент времени, соответствующий 5-му обороту. nср = (n0 + n) / 2, если n0 = 0, то nср = n / 2 N = nср * t1 = (n / 2) * t1 t1 = (2 * N) / n Число оборотов n = ω / (2 * π) = v / (2 * π * R), где ω = v / R Подставляем n в предыдущую формулу и получаем, что: t1 = (2 * N) / (v / (2 * π * R)) = (4 * π * N * R) / v Угловое ускорение во второй точке β = ω1 / t1, где ω1 = v / R β = (v / R) / ((4 * π * N * R) / v) = v2 / (4 * π * N * R2) Тогда получаем an: an = β2 * t 2 * R = (v2 / (4 * π * N * R2))2 * t 2 * R = (v4 * t 2) / (16 * π2 * N2 * R3) = = (34 * 4 2) / (16 * 3,142 * 52 * 0,563) = 1,871 м/с2 Ответ: нормальное ускорение точки равно 1,871 м/с2 (2-й способрешения): Преобразуем нашу окружность в прямую линию (распрямим круг). Тогда длина окружности S получается равна одному обороту. Длину окружности мы можем найти по формуле: S = 2 * π * R Найдем общее пройденное точкой расстояние. Умножаем на количество оборотов (N = 5) на длину окружности: S5 = 2 * π * R * N = 2 * π * R * 5 = 10 * π * R S5 = 10 * π * R Теперь находим тангенциальное ускорение at. Т.к. оно постоянно, следовательно, у нас равноускоренное движение. При равноускоренном движении линейная скорость после пяти оборотов равна: v5 = √2 * at * S5 at = v52 / 2 * S5 Теперь найдем линейную скорость точки через 4 с после начала движения: v4 = at * t Подставляем в эту формулу at вычисленную ранее и получаем: v4 = (v52 / 2 * S5) * t = (v52 / 2 * 10 * π * R) * t = (v52 / 20 * π * R) * t v4 = (32 / 20 * 3.14 * 0,56) * 4 = 1,02366 м/с Теперь найдем нормальное ускорение точки an через радиус кривизны. В нашем случае радиус кривизны, это наш радиус R: v4 = √R * an an = v42 / R Подставляем найденное значение v4 и получаем: an = (1,02366)2 / 0,56 = 1,871 м/с2 Ответ: нормальное ускорение точки равно 1,871 м/с2 |
