Главная страница
Навигация по странице:

  • 2.В тундре жили 14 оленей и 9 лосей. Умерло 10 зверей. Какова вероятность, что среди уцелевших 2 лося

  • 3.Вероятность прорыва канализационной трубы равна 0,4, вероятность нашествия клопов - 0,6, обвала потолка - 0,2. Какова вероятность, что ничего не случится

  • 4.Вероятность того, что змея умрет в первом террариуме равна 1/5, во втором террариуме - 1/7, в третьем террариуме – 1/4. Змею поместили в один из террариумов. Какова вероятность выжить

  • 5.В условиях предыдущей задачи змея умерла. Какова вероятность того, что она умерла в третьем террариуме

  • 6.7% австралийцев – бушмены. Какова вероятность того, что среди 4 австралийцев будет хотя бы 1 бушмен

  • 7.9% жителей Техаса – индейцы. Какова вероятность, что среди 1000 техасцев индейцев будет: а)70; б) от 60 до 95.

  • 8.

  • 9.Гости могут прийти в любой момент , начиная с 11.00 до 22.00. Найти вероятность того, что они придут с 13.00 до 17.23.

  • 10. Ошибки измерения нормальны с а=0

    		•

    Решение Воспользуемся формулой классической вероятности


    Скачать 229.92 Kb.
    НазваниеРешение Воспользуемся формулой классической вероятности
    Дата05.12.2021
    Размер229.92 Kb.
    Формат файлаdocx
    Имя файлаreshenie.docx
    ТипРешение
    #292400

    1.В лесу жили 6 бакланов и 8 тушканчиков. 5 из них поймали и съели. Какова вероятность, что это были бакланы? Что среди них было хотя бы 3 тушканчика?

    Решение: Воспользуемся формулой классической вероятности: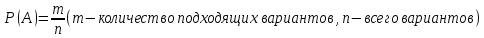



    А={событие заключающееся в том, что хотя бы 3 из 5 пойманных жителей леса были тушканчики}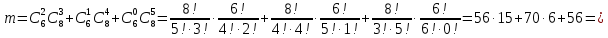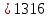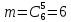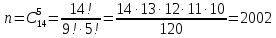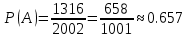











    B={событие заключающееся в том, что съели 5 бакланом}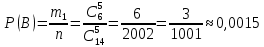



    Ответ: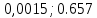

    2.В тундре жили 14 оленей и 9 лосей. Умерло 10 зверей. Какова вероятность, что среди уцелевших 2 лося?

    Решение: Воспользуемся формулой классической вероятности: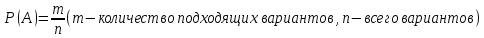



    А={событие заключающееся в том, уцелело два лося}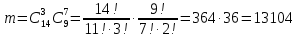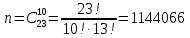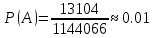







    Ответ: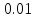

    3.Вероятность прорыва канализационной трубы равна 0,4, вероятность нашествия клопов - 0,6, обвала потолка - 0,2. Какова вероятность, что ничего не случится?

    Решение: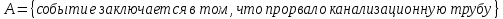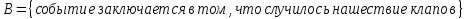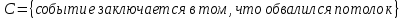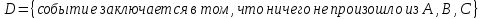







    Р(А)=0.4; Р(В)=0.6; Р(В)=0.2;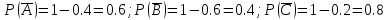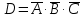





    Используем то, что события независимы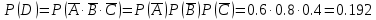



    Ответ: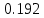

    4.Вероятность того, что змея умрет в первом террариуме равна 1/5, во втором террариуме - 1/7, в третьем террариуме – 1/4. Змею поместили в один из террариумов. Какова вероятность выжить?

    Решение: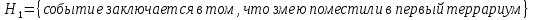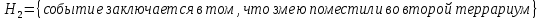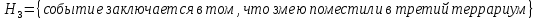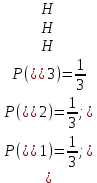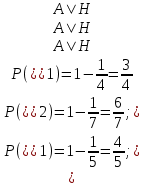













    Воспользуемся формулой полной вероятности: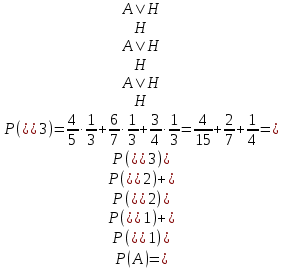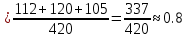





    Ответ: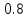

    5.В условиях предыдущей задачи змея умерла. Какова вероятность того, что она умерла в третьем террариуме?

    Решение: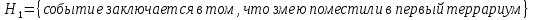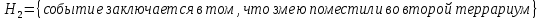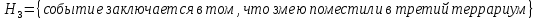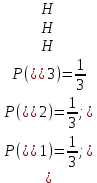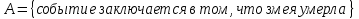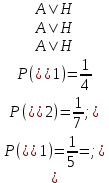













    Воспользуемся формулой Баесса: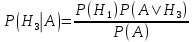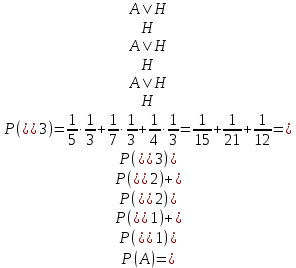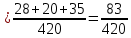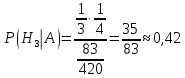









    Ответ: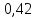

    6.7% австралийцев – бушмены. Какова вероятность того, что среди 4 австралийцев будет хотя бы 1 бушмен?

    Решение:

    Для решения воспользуемся формулой Бернулли: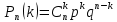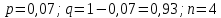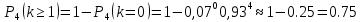







    Ответ:

    7.9% жителей Техаса – индейцы. Какова вероятность, что среди 1000 техасцев индейцев будет: а)70; б) от 60 до 95.

    Решение: а) для решения используем локальную теорему Муавра –Лапласа: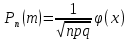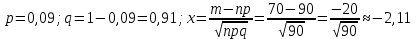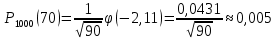







    б) воспользуемся интегральной теоремой Муавра-Лапласа: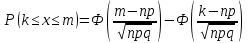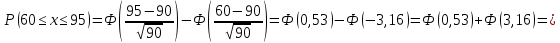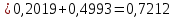







    8.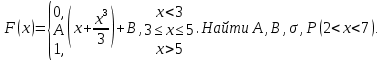

    Решение:

    1)Определим А и В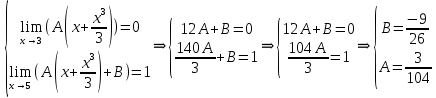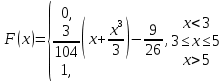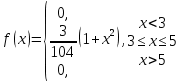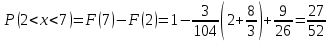









    вычислим среднеквадратическое отклонение: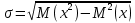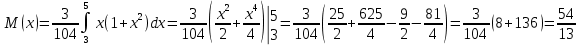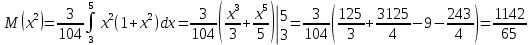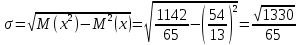









    Ответ: А=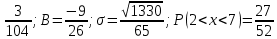

    9.Гости могут прийти в любой момент, начиная с 11.00 до 22.00. Найти вероятность того, что они придут с 13.00 до 17.23.

    Решение: Найдем длину промежутка в который должны прийти гости в минутах: 660 минут

    А с 13.00 до 17.23 время в минутах равно: 263 минуты, тогда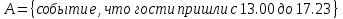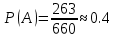





    Ответ: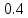

    10. Ошибки измерения нормальны с а=0, σ=6 В. Найти вероятность того, что в 2 независимых измерениях ошибка будет не более 14 В.

    Решение: Найдем вероятность того, что при одном эксперименте отклонение будет не более 14В.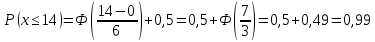



    Тогда вероятность, что при двух независимых испытаниях, получим ошибку меньше 14 будет равна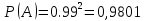



    Ответ: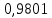


    написать администратору сайта