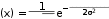|
Решение Воспользуемся свойствами () 0, ( ) 1 , () Тогда
Задание №1. Найти производную функции: 𝑦 = 𝑐𝑜𝑠(𝑥2 + 3)
Решение
Воспользуемся свойствами
(𝑎)′ = 0, (𝑢𝑎)′ = 𝑎𝑢𝑎−1 ∙ 𝑢′, (𝑐𝑜𝑠𝑢)′ = −𝑠𝑖𝑛𝑢 ∙ 𝑢′
Тогда:
𝑦′ = −𝑠𝑖𝑛(𝑥2 + 3) ∙ (2𝑥 + 0) = −2𝑥 ∙ 𝑠𝑖𝑛(𝑥2 + 3)
Задание №2. Найти производную функции: 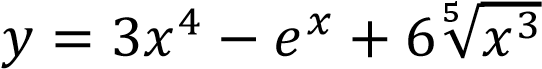
Решение
Воспользуемся свойствами
(𝑢𝑎)′ = 𝑎𝑢𝑎−1 ∙ 𝑢′, (𝑒𝑢)′ = 𝑒𝑢 ∙ 𝑢′
Тогда:
𝑦 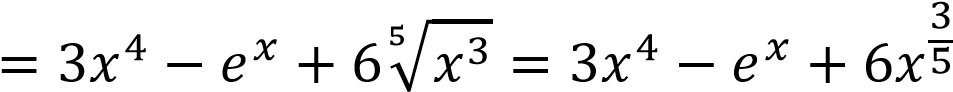
𝑦′ 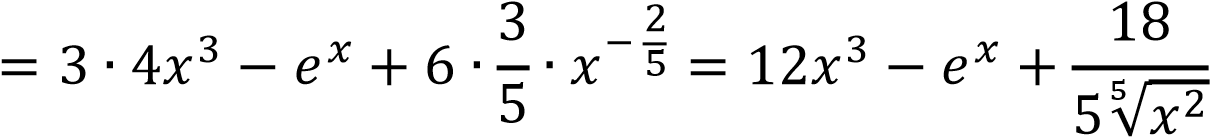
Задание №3. Найти производную функции: 𝑦 = 𝑠𝑖𝑛(2𝑥) ∙ 4𝑥 + 𝑙𝑛3
Решение
Воспользуемся свойствами
(𝑎)′ = 0, (𝑢𝑣)′ = 𝑢′𝑣 + 𝑢𝑣′, (𝑎𝑢)′ = 𝑎𝑢 ∙ 𝑙𝑛𝑎 ∙ 𝑢′, (𝑠𝑖𝑛𝑢)′ = 𝑐𝑜𝑠𝑢 ∙ 𝑢′
Тогда:
𝑦′ = 𝑐𝑜𝑠(2𝑥) ∙ 2 ∙ 4𝑥 + 𝑠𝑖𝑛(2𝑥) ∙ 4𝑥 ∙ 𝑙𝑛4 + 0 =
= 4𝑥 ∙ (𝑐𝑜𝑠(2𝑥) ∙ 2 + 𝑠𝑖𝑛(2𝑥) ∙ 2𝑙𝑛2) = 2 ∙ 4𝑥 ∙ (𝑐𝑜𝑠(2𝑥) + 𝑠𝑖𝑛(2𝑥) ∙ 𝑙𝑛2)
Задание №4. Дано уравнение движения тела: 𝑆 = 2𝑡3 + 3𝑡2 + 2. Найдите скорость и ускорение тела через 2 секунды.
Решение
Скорость равна первой производной от заданного уравнения движения.
𝑣(𝑡) = (2𝑡3 + 3𝑡2 + 2)′𝑡 = 6𝑡2 + 6𝑡
Ускорение равно первой производной от уравнения скорости.
𝑎(𝑡) = (6𝑡2 + 6𝑡)′𝑡 = 12𝑡 + 6
при 𝑡0 = 2 получим:
𝑣(2) = 6 ∙ 22 + 6 ∙ 2 = 36
𝑎(2) = 12 ∙ 2 + 6 = 30
Задание №5. Количество вещества, получаемого в химической реакции, меняется со временем по следующему закону: 𝑄(𝑡) = 4(1 + 8𝑒−16𝑡). Как меняется со временем скорость реакции?
Решение
Скорость реакции равна первой производной от заданного уравнения.
𝑣(𝑡) = (4(1 + 8𝑒−16𝑡))′ = 4 ∙ (0 + 8 ∙ 𝑒−16𝑡 ∙ (−16)) = −512 ∙ 𝑒−16𝑡
𝑡
Задание №6. Развитие патологического процесса со временем описывается уравнением: 𝑦 = 𝑡3 − 𝑡2 + 1. Найти его скорость через 2 секунды от начала развития.
Решение
Скорость равна первой производной от заданного уравнения движения.
𝑣(𝑡) = (𝑡3 − 𝑡2 + 1)′𝑡 = 3𝑡2 − 2𝑡
при 𝑡0 = 2 получим:
𝑣(2) = 3 ∙ 22 − 2 ∙ 2 = 8
Задание №7. Найти дифференциал функции: 𝑦 = 𝑙𝑛𝑥 ∙ 𝑎𝑟𝑐𝑡𝑔𝑥.
Решение
Дифференциал первого порядка имеет вид:
𝑑𝑦 = 𝑦′𝑑𝑥
Найдем первую производную функции:
1 1 𝑎𝑟𝑐𝑡𝑔𝑥 𝑙𝑛𝑥
𝑦′ = 𝑥 ∙ 𝑎𝑟𝑐𝑡𝑔𝑥 + 𝑙𝑛𝑥 ∙ 1 ∙ 𝑎𝑟𝑐𝑡𝑔𝑥 + 𝑙𝑛𝑥 ∙ 1 + 𝑥2 = 𝑥 + 1 + 𝑥2 + 𝑥2 = 𝑥 + 1 + 𝑥2
Тогда:
𝑎𝑟𝑐𝑡𝑔𝑥 𝑙𝑛𝑥
𝑑𝑦 = (  𝑥 + 1 + 𝑥2) 𝑑𝑥 𝑥 + 1 + 𝑥2) 𝑑𝑥
Задание №8. Найти дифференциал функции: 𝑦 = 𝑙𝑛(𝑥3 + 1).
Решение
Дифференциал первого порядка имеет вид:
𝑑𝑦 = 𝑦′𝑑𝑥
Найдем первую производную функции:
𝑦
 
′ = 𝑥31+ 1 ∙ (3𝑥2 + 0) = 𝑥33 𝑥+21
Тогда:
3𝑥2
𝑑𝑦 = 𝑥 3 + 1 𝑑𝑥 3 + 1 𝑑𝑥
Задание №9. Найти приращение функции 𝑦 = (3𝑥2 − 2)3, если ее аргумент изменяется от 1 до 1,001.
Решение
Приращение ∆𝑦 равно в общем виде
∆𝑦 = 𝑦′ ∙ ∆𝑥
Первая производная 𝑦′ равна:
𝑦′ = 3 ∙ (3𝑥2 − 2)2 ∙ (6𝑥 − 0) = 18𝑥 ∙ (3𝑥2 − 2)2
Тогда искомое приращение ∆𝑦 равно:
∆𝑦 = 18𝑥 ∙ (3𝑥2 − 2)2 ∙ ∆𝑥 = 18 ∙ 1 ∙ (3 ∙ 12 − 2)2 ∙ (1,001 − 1) =
= 18 ∙ 0,001 = 0,018
Задание №10. Вычислить интеграл:
𝜋
∫ 𝑠𝑖𝑛𝑥 ∙ 𝑐𝑜𝑠3𝑥 𝑑𝑥 0
Решение
Воспользуемся заменой 𝑐𝑜𝑠𝑥 = 𝑡, тогда −𝑠𝑖𝑛𝑥𝑑𝑥 = 𝑑𝑡. При 𝑥 = 0 получим 𝑡 =
1. При 𝑥 = 𝜋 получим 𝑡 = −1. Тогда
𝜋
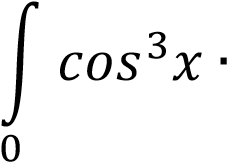 𝑠𝑖𝑛𝑥 𝑑𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
= −  ((−1)4 − 14) = − ((−1)4 − 14) = −  (1 − 1) = 0 (1 − 1) = 0
Задание №11. Найти определенный интеграл:
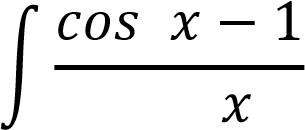 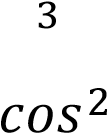 𝑑𝑥 𝑑𝑥
Решение
Преобразуем подынтегральное выражение и, непосредственно интегрируя, получим:
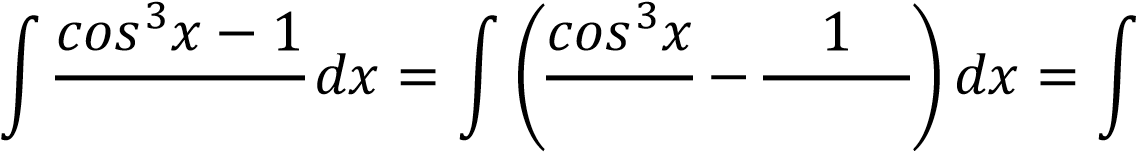 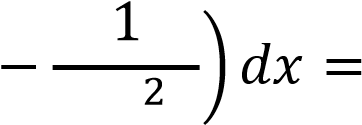 2𝑥 𝑐𝑜𝑠2𝑥 𝑐𝑜𝑠2𝑥 (𝑐𝑜𝑠𝑥 𝑐𝑜𝑠 𝑥 2𝑥 𝑐𝑜𝑠2𝑥 𝑐𝑜𝑠2𝑥 (𝑐𝑜𝑠𝑥 𝑐𝑜𝑠 𝑥
𝑐𝑜𝑠
1
= ∫ 𝑐𝑜𝑠𝑥 𝑑𝑥 − ∫ 𝑐𝑜𝑠 2𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥 − 𝑡𝑔𝑥 + 𝐶 2𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥 − 𝑡𝑔𝑥 + 𝐶
Задание №12. Найти неопределенный интеграл
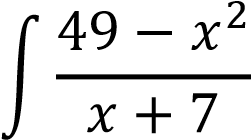 𝑑𝑥 𝑑𝑥
Решение
Преобразуем подынтегральное выражение и, непосредственно интегрируя, получим:
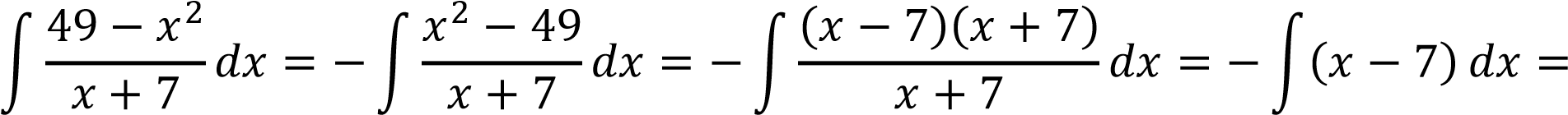
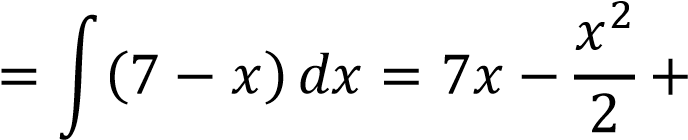 𝐶 𝐶
Задание №13. Вычислить объем тела, образуемого вращением вокруг оси 𝑂𝑋 трапеции, ограниченной линиями:
𝑥
𝑦 =  + 4, 𝑦 = 0, 𝑥 = 0, 𝑥 = 6 + 4, 𝑦 = 0, 𝑥 = 0, 𝑥 = 6
2
Решение
Изобразим заданную фигуру и определим пределы интегрирования: 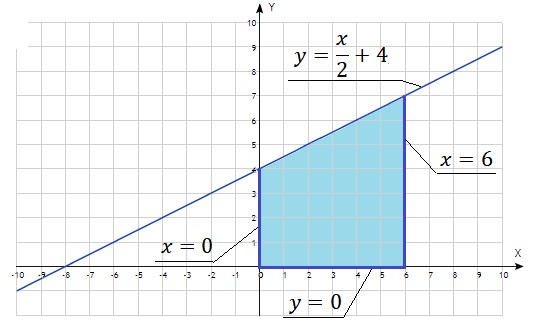
0 ≤ 𝑥 ≤ 6
Объем тела, полученного вращением линии 𝑦 = 𝑓(𝑥) вокруг оси 𝑂𝑥, равен:
𝑏
𝑉𝑥 = 𝜋 ∫ 𝑦2𝑑𝑥
𝑎
𝑉𝑥 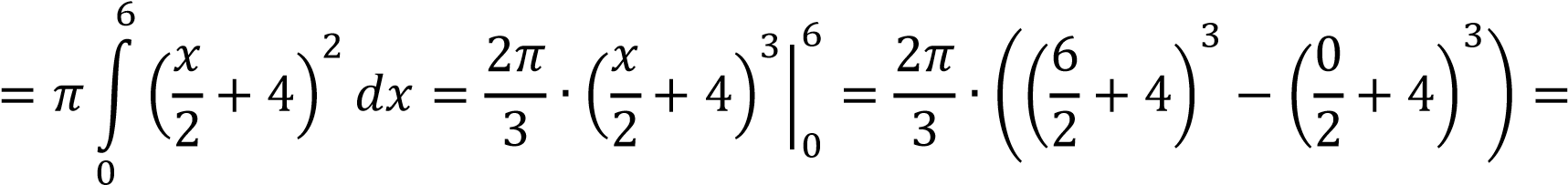
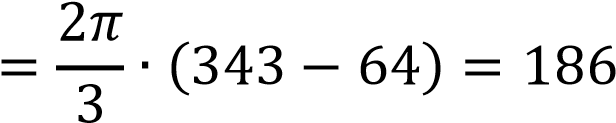 𝜋 (куб. ед. ) 𝜋 (куб. ед. )
Задание №14. Вычислить работу переменной силы 𝑓(𝑥) = 𝑒2𝑥 при прямолинейном перемещении материальной точки из положения с абсциссой
𝑥1 = 0 в положение с абсциссой 𝑥2 = 3.
Решение
Работу силы 𝐹̅ найдем по формуле
𝐴 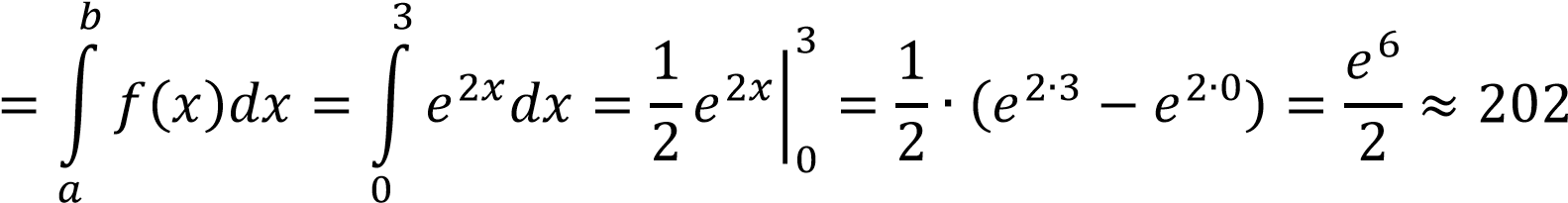 Дж Дж
Задание №15. Найти общее решение дифференциального уравнения:
𝑦′ = 𝑥 ∙ 𝑦
Решение
Преобразуем исходное уравнение
𝑑𝑦
 = 𝑥 ∙ 𝑦 = 𝑥 ∙ 𝑦
𝑑𝑥
𝑑𝑦
 = 𝑥𝑑𝑥 = 𝑥𝑑𝑥
𝑦
Это уравнение с разделяющимися переменными. Интегрируя, имеем
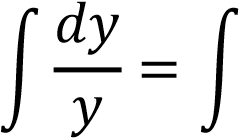 𝑥𝑑𝑥 𝑥𝑑𝑥
𝑥2
𝑙𝑛|𝑦| 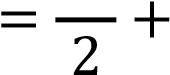 𝐶 𝐶
Тогда общее решение дифференциального уравнения имеет вид:
𝑥2
𝑦 = 𝑒 2 +𝐶
Задание №
. Найти частное решение уравнения
 ′ = 𝑦 ′ = 𝑦
𝑦
𝑥 + 1
удовлетворяющее условию 𝑦(2) = 6.
Решение
Преобразуем исходное уравнение
𝑑𝑦 𝑦
 = =
𝑑𝑥 𝑥 + 1
𝑑𝑦 𝑑𝑥
 = =
𝑦 𝑥 + 1
Это уравнение с разделяющимися переменными. Интегрируя, имеем
𝑑𝑦 𝑑𝑥
∫  = ∫ = ∫ 
𝑦 𝑥 + 1
𝑙𝑛|𝑦| = 𝑙𝑛|𝑥 + 1| + 𝑙𝑛|𝐶|
Тогда общее решение дифференциального уравнения имеет вид:
𝑦 = 𝐶 ∙ (𝑥 + 1)
Из начального условия 𝑦(2) = 6 получим:
𝐶 ∙ (2 + 1) = 6
𝐶 = 2
Тогда частное решение дифференциального уравнения, удовлетворяющее начальному условию, имеет вид:
𝑦 = 2 ∙ (𝑥 + 1)
. Популяция бактерий растет так, что скорость ее роста в момент
времени 𝑡 равна 0,1 от размера популяции 𝑥(𝑡) . Опишите этот процесс с помощью дифференциального уравнения, если 𝑥(0) = 1000.
Решение
Пусть закон изменения числа бактерий имеет вид
𝑥 = 𝑥(𝑡)
Поскольку скорость изменения числа бактерий 𝑥′ пропорциональна числу бактерий 𝑥 в текущий момент времени 𝑡 с коэффициентом пропорциональности 𝑘 = 0,1, тогда по условию задачи составим уравнение:
𝑥′ = 0,1𝑥
𝑑𝑥
 = 0,1𝑑𝑡 = 0,1𝑑𝑡
𝑥
Интегрируя, имеем
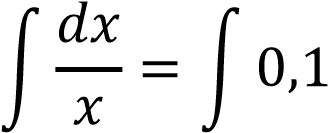 𝑑𝑡 𝑑𝑡
𝑙𝑛𝑥 = 0,1𝑡 + 𝑙𝑛𝐶
Тогда общее решение дифференциального уравнения имеет вид:
𝑥 = 𝐶𝑒0,1𝑡
Из начального условия 𝑥(0) = 1000 имеем
𝐶𝑒0 = 1000
𝐶 = 1000
Тогда заданный процесс можно описать с помощью дифференциального уравнения:
𝑥 = 1000𝑒0,1𝑡
. Студент пришел на экзамен, зная лишь 20 вопросов из 24. В
билете 3 вопроса. Найти вероятность того, что ему в билете попадется хотя бы 1 вопрос, который он не знает.
Решение
Основное событие𝐴 – студенту в билете попадется хотя бы 1 вопрос, который он не знает.
Это событие противоположно событию 𝐴̅ − студент ответит на все 3 вопроса.
Найдем вероятность события 𝐴̅.
По классическому определению вероятности, вероятность события 𝐴̅ равна
𝑚
𝑃(𝐴̅) = 
𝑛
где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов.
Число возможных способов взять 3 вопроса из 24 по формуле сочетаний равна
𝐶243 .
Благоприятствующими являются случаи, когда из общего числа 20 знакомых вопросов в билете оказались 3 (это можно сделать 𝐶203 способами).
𝐶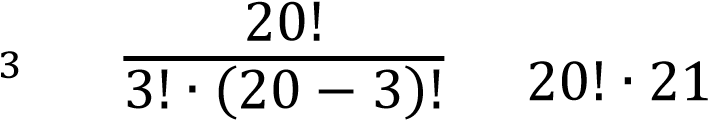 ! 𝑃 ̅ 𝐶 ! 𝑃 ̅ 𝐶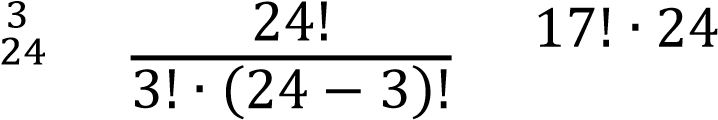 ! !
Вероятность события 𝐴 равна:
𝑃(𝐴) = 1 − 𝑃(𝐴̅) = 1 − 0,5632 = 0,4368
Ответ: 𝑃(𝐴) = 0,4368
. При перевозке 1000 стеклянных ваз вероятность разбить 1 вазу
равна 0,002. Какова вероятность, что будут разбиты 4 вазы?
Решение
Испытание: перевозится 1000 ваз.
Поскольку число испытаний достаточно велико ( 𝑛 = 1000 ), вероятность наступления события постоянна, но мала ( 𝑝 = 0,002 ), произведение
𝑛𝑝 = 2 ≤ 10, то можно применить формулу Пуассона.
Применим формулу Пуассона. Если производится достаточно большое число испытаний (𝑛 – велико), в каждом из которых вероятность наступления события 𝐴 постоянна, но мала, то вероятность того, что в 𝑛 испытаниях событие 𝐴 наступит 𝑚 раз, определяется приближенно формулой
 𝑃𝑛(𝑚) = 𝜆𝑚 −𝜆 где 𝜆 = 𝑛𝑝 𝑃𝑛(𝑚) = 𝜆𝑚 −𝜆 где 𝜆 = 𝑛𝑝
𝑒
𝑚!
Событие𝐴 – будут разбиты 4 вазы.
В данном случае 𝜆 = 𝑛𝑝 = 2

𝑃(𝐴) = 𝑃1000(4) = 2 44! 𝑒−2 = 2416𝑒2 = 32𝑒2 = 0,0902 44! 𝑒−2 = 2416𝑒2 = 32𝑒2 = 0,0902
Ответ: 𝑃(𝐴) = 0,0902
. Известно, что в партии из 1000 ампул с новокаином 400 ампул
изготовлено на одном заводе, 350 – на втором и 250 – на третьем. Известны вероятности 0,75; 0,80; 0,85 того, что ампула окажется без дефекта при изготовлении ее соответственно на первом, втором и третьим заводах. Какова вероятность того, что выбранная наугад из данной партии ампула с новокаином окажется без дефекта.
Решение
Основное событие𝐴 − выбранная наугад из данной партии ампула с новокаином окажется без дефекта.
Гипотезы:
𝐻1 − выбранная ампула поступила с первого завода;
𝐻2 − выбранная ампула поступила со второго завода;
𝐻3 − выбранная ампула поступила с третьего завода.
Вероятности гипотез (по классическому определению вероятности):
𝑃(𝐻1) = 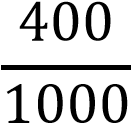 = 0,4 𝑃(𝐻2) = = 0,4 𝑃(𝐻2) = 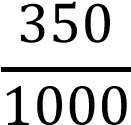 = 0,35 = 0,35
𝑃(𝐻3) = 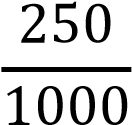 = 0,25 = 0,25
Условные вероятности (по условию):
𝑃𝐻1(𝐴) = 0,75 𝑃𝐻2(𝐴) = 0,8 𝑃𝐻3(𝐴) = 0,85
Вероятность события 𝐴 по формуле полной вероятности равна:
𝑃(𝐴) = 𝑃(𝐻1) ∙ 𝑃𝐻1(𝐴) + 𝑃(𝐻2) ∙ 𝑃𝐻2(𝐴) + 𝑃(𝐻3) ∙ 𝑃𝐻3(𝐴) =
= 0,4 ∙ 0,75 + 0,35 ∙ 0,8 + 0,25 ∙ 0,85 = 0,7925
Ответ: 𝑃(𝐴) = 0,7925
Задание №21. Найти вероятность того, что случайная величина, распределенная по нормальному закону с математическим ожиданием равным 1 и дисперсией равной 4, примет значение от 0 до (–5).
Решение
Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна:
𝑃(𝛼 < 𝑋 < 𝛽) = Ф (𝛽 − 𝑚𝑥) − Ф (𝛼 − 𝑚𝑥) − 𝑚𝑥) − Ф (𝛼 − 𝑚𝑥)
𝜎 𝜎
где Ф(𝑥) – функция Лапласа, 𝑚𝑥 − математическое ожидание; 𝜎 − среднее квадратическое отклонение.
При 𝑚𝑥 = 1; 𝜎 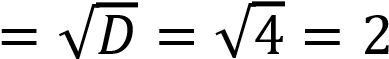 ; 𝛼 = −5; β = 0 получим вероятность попадания случайной величины 𝑋 в заданный интервал: ; 𝛼 = −5; β = 0 получим вероятность попадания случайной величины 𝑋 в заданный интервал:
𝑃(−5 < 𝑋 < 0) = Ф (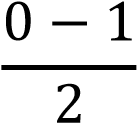 ) − Ф ( ) − Ф (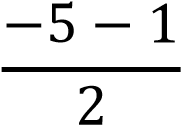 ) = ) =
= Ф(−0,5) − Ф(−3) = Ф(3) − Ф(0,5) = 0,49865 − 0,1915 = 0,30715
Ответ: 𝑃(−5 < 𝑋 < 0) = 0,30715
. Записать плотность распределения вероятностей и функцию
распределения нормально распределенной случайной величины 𝑋 , если 𝑀(𝑋) = 2; 𝐷(𝑋) = 4.
Решение
Плотность распределения вероятности нормально распределенной случайной величины имеет вид
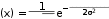
(𝑥−𝑀(𝑋))2
𝑓
𝜎√2𝜋
При 𝑀 получим: получим:
𝑓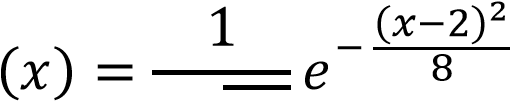
2√2𝜋
. Число звонков на станцию скорой помощи за 15 минут
представлено в виде следующей выборки: 1, 4, 2, 3, 2, 3, 3, 2, 3, 4. Представить данную выборку в виде вариационного и простого статистического ряда. Построить полигон частот.
Решение
Построим вариационный ряд – выборку в порядке возрастания:
1, 2, 2, 2, 3, 3, 3, 3, 4, 4
Запишем простой статистический ряд (зависимость частоты 𝑛𝑖 от значения 𝑥𝑖):
Построим полигон частот.
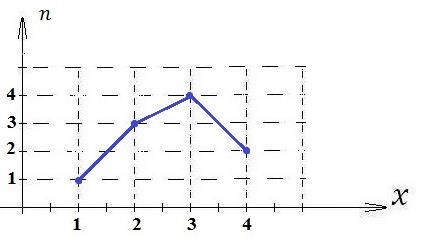
Дана выборка: 12, 10, 17, 13, 20, 18, 25, 27, 24, 30. Найти ее основные числовые характеристики.
Решение
Общее число значений
𝑛 = ∑ 𝑛𝑖 = 10
Найдем выборочную среднюю 𝑥̅.
𝑛
𝑥̅ 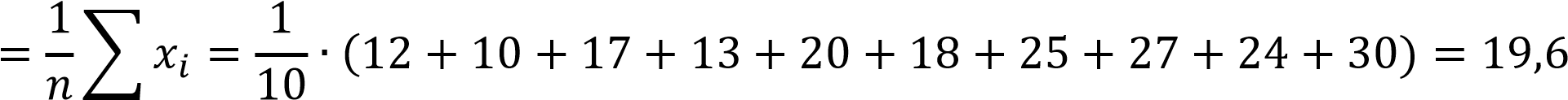
𝑖=1
Выборочная дисперсия равна:
𝑛
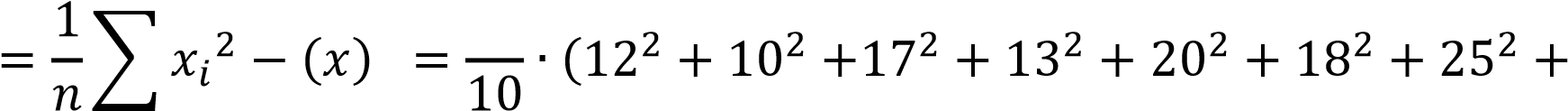 2 1 2 1
𝐷в ̅
𝑖=1
+272 + 242 + 302) − 19,62 = 41,44
Выборочное среднеквадратическое отклонение:
𝜎в 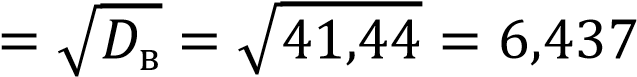
. При измерении частоты пульса получены значения: 71, 70, 74, 70, 72, 71, 70, 73, 72, 70. Составьте простой статистический ряд. Определите выборочное среднее и выборочную дисперсию.
Решение
Построим вариационный ряд – выборку в порядке возрастания:
70, 70, 70, 70, 71, 71, 72, 72, 73, 74
Запишем простой статистический ряд (зависимость частоты 𝑛𝑖 от значения 𝑥𝑖):
𝑥𝑖
|
70
|
71
|
72
|
73
|
74
|
𝑛𝑖
|
4
|
2
|
2
|
1
|
1
|
Общее число значений:
𝑛 = ∑ 𝑛𝑖 = 10
Найдем выборочное среднее:
𝑥̅ 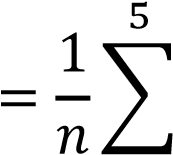 𝑛𝑖𝑥𝑖 𝑛𝑖𝑥𝑖 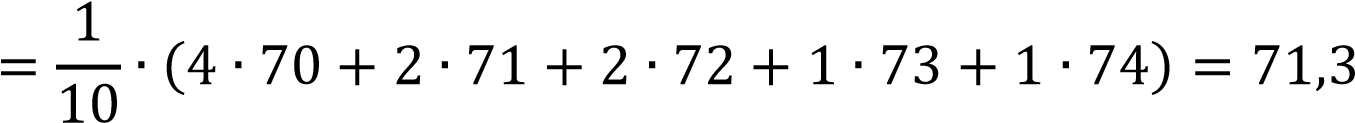
𝑖=1
Найдем выборочную дисперсию:
𝐷в 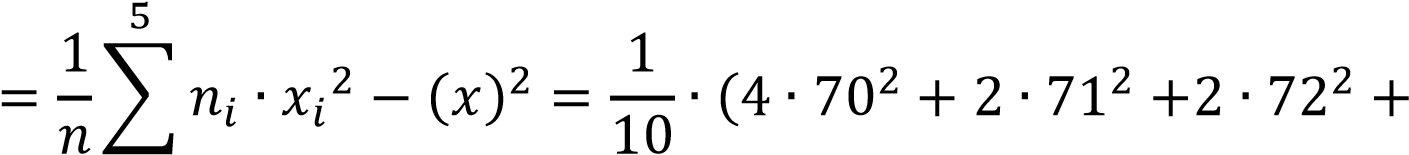 ̅ ̅
𝑖=1
+1 ∙ 732 + 1 ∙ 742) − 71,32 = 1,81
. При измерении частоты дыхания получены значения 12, 14, 12, 15. Представьте выборку в виде вариационного ряда, определите выборочное среднее и выборочную дисперсию.
Решение
Построим вариационный ряд – выборку в порядке возрастания:
12, 12, 14, 15
Общее число значений
𝑛 = ∑ 𝑛𝑖 = 4
Найдем выборочное среднее.
𝑛
𝑥̅ 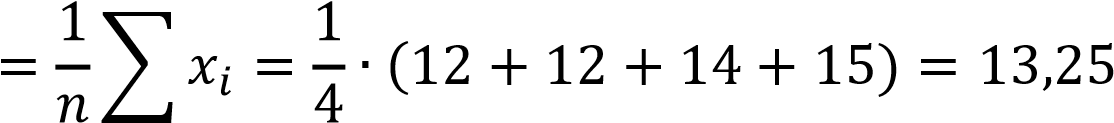
𝑖=1
Выборочная дисперсия равна:
𝑛
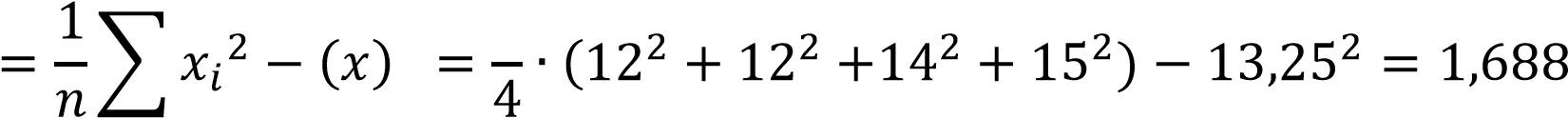 2 1 2 1
𝐷в ̅
𝑖=1
С помощью микроскопа измеряли диаметр эритроцитов человека. При этом были получены следующие значения: 5, 8, 11, 8 мкм. Дайте интервальную оценку размера эритроцитов с доверительной вероятностью 0.95.
Решение
Построим вариационный ряд – выборку в порядке возрастания: 5, 8, 8, 11.
Общее число значений
𝑛 = ∑ 𝑛𝑖 = 4
Найдем выборочное среднее.
𝑛
𝑥̅ 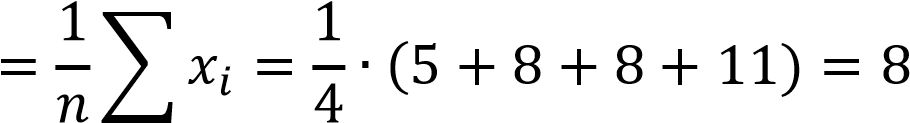
𝑖=1
Выборочная дисперсия равна:
𝑛
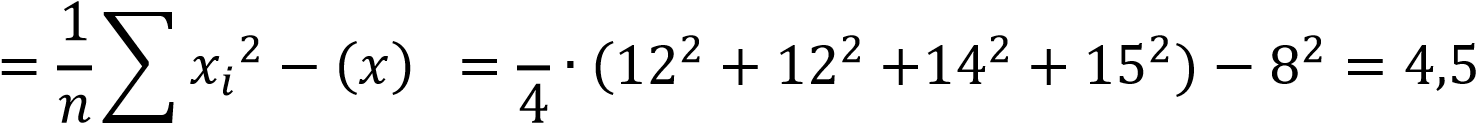 2 1 2 1
𝐷в ̅
𝑖=1
Найдем выборочную несмещённую 𝑆2 (исправленную) дисперсию:
𝑆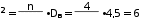
𝑛 − 1 4 − 1
Исправленное среднее квадратическое отклонение равно:
𝑠 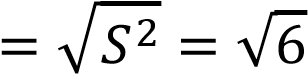
Доверительный интервал для математического ожидания 𝑎 равен:
𝑡𝛾,𝑛−1𝑠 𝑡𝛾,𝑛−1𝑠
𝑥̅ 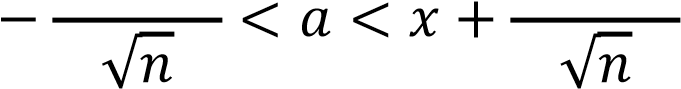 ̅ ̅
где 𝑡𝛾,𝑛−1 – значение, определяемое по таблице квантилей распределения Стьюдента в зависимости от числа степеней свободы ( 𝑛 − 1 = 3 ) и доверительной вероятности 𝛾 = 0,95.
По таблице квантилей распределения Стьюдента находим: 𝑡𝛾,𝑛−1 = 𝑡(0,95; 3) = 3,18
и искомый доверительный интервал имеет вид:
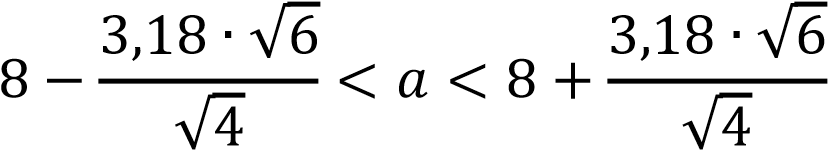
4,105 < 𝑎 < 11,895
Задание №28. При исследовании проницаемости сосудов сетчатки была получена следующая выборка: 14, 12, 16, 11, 15, 17, 13, 15, 16, 11. Считая, что данный признак распределен нормально со средним квадратическим разбросом равным 5, найти доверительный интервал для оценки неизвестного математического ожидания с доверительной вероятностью 0,95.
Решение
Построим вариационный ряд – выборку в порядке возрастания:
11, 11, 12, 13, 14, 15, 15, 16, 16, 17.
Запишем простой статистический ряд (зависимость частоты 𝑛𝑖 от значения 𝑥𝑖):
𝑥𝑖
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
𝑛𝑖
|
2
|
1
|
1
|
1
|
2
|
2
|
1
|
Общее число значений: 𝑛 = 10. Найдем выборочное среднее:
𝑥̅ 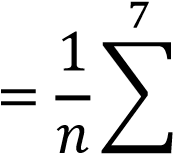 𝑛𝑖𝑥𝑖 𝑛𝑖𝑥𝑖 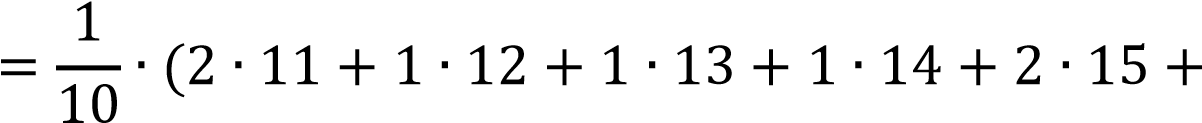
𝑖=1
+2 ∙ 16 + 1 ∙ 17) = 14
Полагая средний квадратический разброс 𝜎в∗ = 5, получим доверительный интервал для математического ожидания 𝑎:
𝑡𝜎∗ 𝑡𝜎∗
𝑥̅ 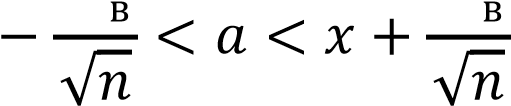 ̅ ̅
где 𝑡 – такое значение аргумента функции Лапласа, при котором Ф(𝑡) =  𝛾. 𝛾.
По таблице функции Лапласа находим 𝑡 из равенства:
Ф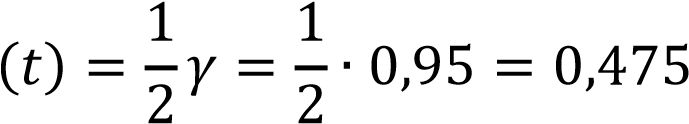
Получаем 𝑡 = 1,96, и искомый доверительный интервал имеет вид:
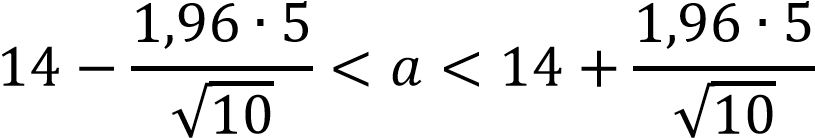
10,9 < 𝑎 < 17,1 |
|
|
 Скачать 443.05 Kb.
Скачать 443.05 Kb.
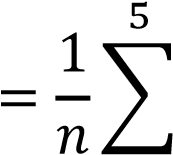 𝑛𝑖𝑥𝑖
𝑛𝑖𝑥𝑖 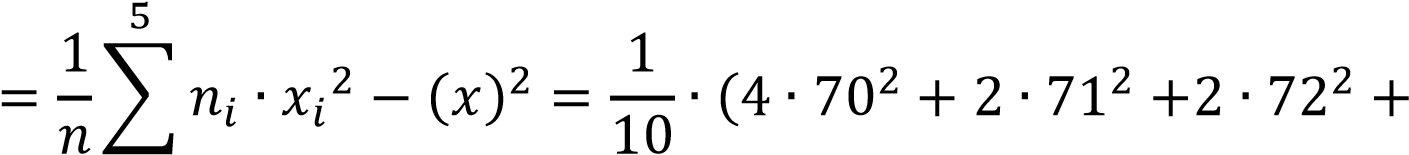 ̅
̅ 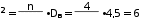

 ∙ 𝑎𝑟𝑐𝑡𝑔𝑥 + 𝑙𝑛𝑥 ∙ 1
∙ 𝑎𝑟𝑐𝑡𝑔𝑥 + 𝑙𝑛𝑥 ∙ 1 + 𝑥2 = 𝑥 + 1 + 𝑥2
+ 𝑥2 = 𝑥 + 1 + 𝑥2  𝑥 + 1 + 𝑥2) 𝑑𝑥
𝑥 + 1 + 𝑥2) 𝑑𝑥 
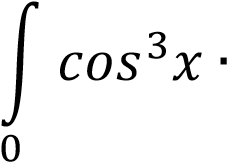 𝑠𝑖𝑛𝑥 𝑑𝑥
𝑠𝑖𝑛𝑥 𝑑𝑥  2𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥 − 𝑡𝑔𝑥 + 𝐶
2𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥 − 𝑡𝑔𝑥 + 𝐶 
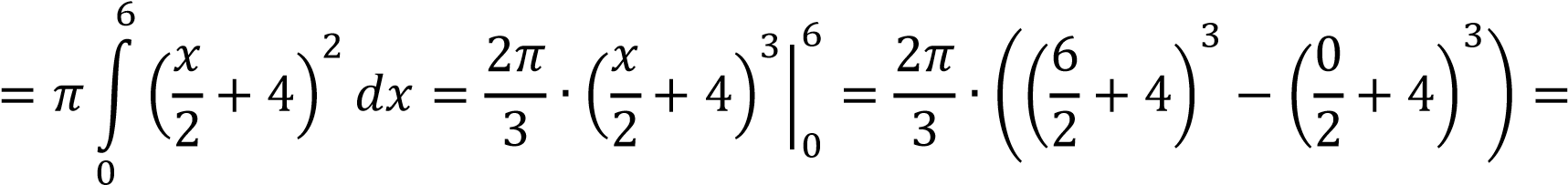
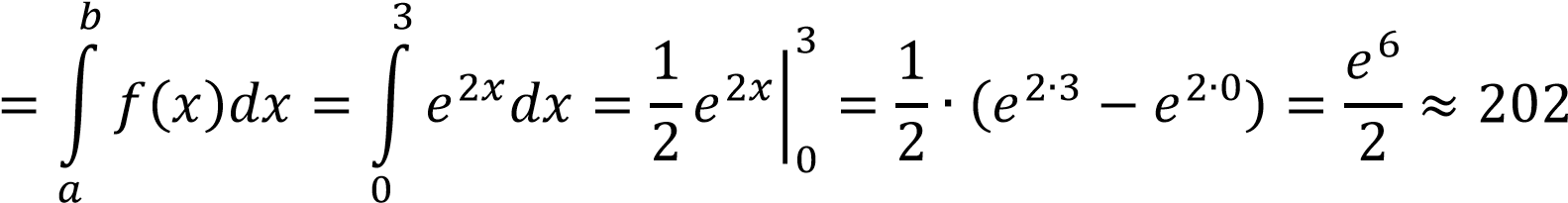 Дж
Дж  = 𝑥 ∙ 𝑦
= 𝑥 ∙ 𝑦  ′ = 𝑦
′ = 𝑦  =
= 
 𝑃𝑛(𝑚) = 𝜆𝑚 −𝜆 где 𝜆 = 𝑛𝑝
𝑃𝑛(𝑚) = 𝜆𝑚 −𝜆 где 𝜆 = 𝑛𝑝 
 44! 𝑒−2 = 2416𝑒2 = 32𝑒2 = 0,0902
44! 𝑒−2 = 2416𝑒2 = 32𝑒2 = 0,0902  − 𝑚𝑥) − Ф (𝛼 − 𝑚𝑥)
− 𝑚𝑥) − Ф (𝛼 − 𝑚𝑥)