Комбинаторика и теория графов. Решение Введем обозначения для элементарных высказываний Захватить противника врасплох А
 Скачать 119.59 Kb. Скачать 119.59 Kb.
|
|
«–» – отсутствие символа или символ, не принадлежащий алфавиту {a, b}; a(t) – входной символ; q(t) – исходное состояние; q(t + 1) – последующее состояние. Проверим работу автомата. Пусть задано слово аbb:
q5 – заключительное состояние, следовательно, слово распознано. Задано слово аа-:
q2 – не заключительное состояние, перейти из него можно только в q2, поэтому слово не распознано. 8. Описать конечный автомат, распознающий язык, заданный регулярным выражением: (а + b + cd*)* Решение: Граф конечного (недетерминированного) автомата, распознающего язык, заданный данным регулярным выражением, имеет вид: 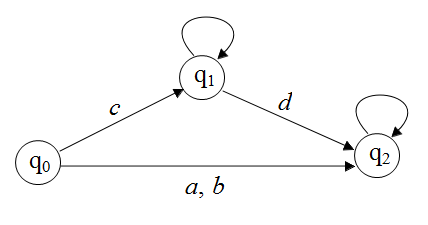 Автомат имеет три состояния, из них q0 – начальное состояние, q2 – заключительное состояние. 1) Из начального состояния при подаче на вход символов а и b автомат переходит в заключительное состояние q2; 2) Из начального состояния при подаче на вход символа c автомат переходит в состояние q1; 3) Из состояния q1 при подаче на вход символа d автомат переходит в состояние q1; 4) Из состояния q1 при подаче на вход символа d автомат переходит в заключительное состояние q2; 5) Из состояния q2 при подаче на вход символов а, b иd автомат переходит в заключительное состояние q2. 9. Построить порождающую грамматику для языка L = {(ac)n (cb)n, n > 0}. Решение: Выражения (ac)n и (cb)n означают повторение n раз пар символов ac и cb. Таким образом, язык L состоит из цепочек вида accb, acaccbcb и т.д. Зададим КС-грамматику для этого языка. Заметим, что из одной цепочки языка можно получить другую, присоединяя к первой слева символы aс, а справа символы сb. Например, если имеется цепочка acaccbcb, из нее можно получить цепочку асacaccbcbcb. Это замечание дает правило порождения S → aсSсb (т.к. цепочки языка порождаются из начального нетерминала грамматики и, значит, могут быть обозначены этим символом). Есть еще специальный случай цепочки, которая не дробится на более мелкие – это цепочка ассb. Для ее порождения введем правило S → aссb. Итак, грамматика языка имеет правила: S → aсSсb и S → aссb. Зададим порождение цепочки aсaсaссbсbсb: S aсSсb aсaсSсbсb aсaсaссbсbсb. 10. Описать язык, который определяет КС грамматика S::= 0|S0S. Удовлетворяет ли она условию однозначности ветвления по первому символу. Решение: Грамматика языка в форме Бэкуса-Наура: <буква>::= <цифра>|(<буква><цифра><буква>). <буква>::= S, <цифра>::= 0. Грамматика удовлетворяет условию однозначности ветвления по первому символу, так как L(<буква>) ≠ L(<цифра>), то есть L(<буква>) ∩ L(<цифра>) = . 11. Для грамматики, заданной следующими правилами вывода, построить эквивалентный ей конечный автомат: S → bS|aA|a|b, A → aA|bS|a Решение: Для грамматики, заданной следующими правилами вывода, S → bS|aA|a|b, A → aA|bS|a построим эквивалентный ей конечный автомат. Граф автомата имеет три вершины, две из которых помечены нетерминальными символами S и А, а третья вершина, помеченная символом F (final), – это заключительное состояние. Начальное состояние – это вершина S, соответствующая аксиоме грамматики S. Каждому правилу грамматики ставится в соответствие команда конечного автомата: 1) Sb →S: в начальном состоянии при подаче на вход терминального символа b автомат остается в состоянии S; 2) Sa → A: из начального состояния при подаче на вход терминального символа a автомат переходит в состояние А; 3) Sa → F: из начального состояния при подаче на вход терминального символа a автомат переходит в заключительное состояние F; 4) Sb → F: из начального состояния при подаче на вход терминального символа b автомат переходит в заключительное состояние F; 5) Аa →А: из состояния А при подаче на вход терминального символа a автомат остается в состоянии А; 6) Аb →S: из состояния А при подаче на вход терминального символа b автомат переходит в состояние S; 7) Аa →F: из состояния А при подаче на вход терминального символа a автомат переходит в заключительное состояние F.  Получившийся недетерминированный конечный автомат распознает цепочки символов, заданные правилами вывода данной грамматики. 12. Дана инфиксная скобочная форма записи арифметического выражения: (a + b*c)/(d – e – f) Перевести ее в постфиксную форму. Решение: Существуют 3 основных формы записи выражений: инфиксная, постфиксная, префиксная. Префиксы «пре-», «пост-» и «ин-» относятся к относительной позиции оператора по отношению к обоим операндам. Следовательно, в постфиксной записи операция следует за обоими операндами. Форму записи алгебраических выражений со знаком операции после операндов называют постфиксной, или обратной польской записью. Постфиксная форма записи арифметического выражения (a + b*c)/(d – e – f): (a + b*c)/(d – e – f) = abc*+ de – f – /. Сначала идет оператор *, относящийся к операндам b и c. Затем идет оператор +, относящийся к операндам a и b*c. После этого осуществляется вычитание операндов d и e и d – e и f. Последний символ в постфиксе – символ /, задающий деление операнда abc*+ на операнд de – f –. |
