Комбинаторика и теория графов. Решение Введем обозначения для элементарных высказываний Захватить противника врасплох А
 Скачать 119.59 Kb. Скачать 119.59 Kb.
|
|
2.2. Второй вариант 1. Будет ли логичным следующее рассуждение: Намеченная атака удастся, если захватить противника врасплох или его позиции плохо защищены. Захватить противника врасплох можно только, если он беспечен. Он не будет беспечен, если его позиции плохо защищены. Следовательно, намеченная атака не удастся. Решение: 1. Введем обозначения для элементарных высказываний: «Захватить противника врасплох» – А; «Позиции врага плохо защищены» – В; «Противник беспечен» – С; «Намеченная атака удастся» – D. Формализуем посылки и заключение: (А В) D – посылка; C A – посылка; B C – посылка; D – заключение. Тогда логическая схема рассуждения такова: (А В) D, C A, B C 2. Запишем формулу в виде конъюнкции посылок, ведущих к заключению: ((А В) D)&(C A)&(B C) D. Построим таблицу истинности полученного выражения, предварительно введя обозначения для подформул: (А В) D = Е, C A = F, B C = G, ((А В) D)&(C A)&(B C) = H.
Так как формула принимает значение 1 не на всех наборах переменных, она не является тождественно истинной (тавтологией). Следовательно, заключение не следует из посылок и рассуждение неправильное. 2. Провести исследование булевой функции f(x, y, z) = ((z y) x)((xy) (z x)): a. построить таблицу функции; ответ записать в виде набора значений, упорядоченного в соответствии с лексикографическим порядком набора аргументов; b. построить СДНФ этой функции; ответ записать, упорядочив элементарные конъюнкции в лексикографическом порядке; c. упростить полученное выражение с помощью метода минимизирующих карт, ответ записать в виде минимальной ДНФ; d. построить многочлен Жегалкина исходной функции; e. построить таблицу двойственной функции; ответ записать в виде упорядоченного набора значений; f. построить СКНФ двойственной функции; ответ записать, упорядочив элементарные дизъюнкции в лексикографическом порядке; g. проверить исходную функцию на принадлежность основным классам замкнутости T0,T1, L, M, S; h. Выразить отрицание h(x) = x и конъюнкцию g(x, y) = xy через функцию f(x, y, z) и ее отрицание. Решение: а. Таблица функции f(x, y, z) = ((z y) x)((xy) (z x)):
b. Построим СДНФ по таблице функции. СДНФ – дизъюнкция элементарных конъюнкций (минтермов, конституент единицы). В СДНФ входят наборы переменных, на которых значение функции равно 1, причем, если значение переменной равно 1, то она входит в минтерм без отрицания, а если 0 – то с отрицанием. Для данной функции единичные значения определяются на наборах 001 (1), 100 (4) и 101 (5): fСДНФ(x, y, z) = ͞x ͞y z x ͞y ͞z x ͞y z. c. Упростим полученное выражение с помощью метода минимизирующих карт.     Строим для функции минимизирующую карту: Строим для функции минимизирующую карту: 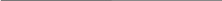 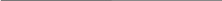 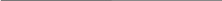 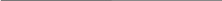
Отметим в последнем столбце те конъюнкции, которые входят в СДНФ данной функции. Вычеркнем неотмеченные строки, затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки. fМДНФ(x, y, z) = x ͞y ͞y z. Упростим СДНФ, используя карту Карно. На карте Карно отыскиваются квадраты и/или прямоугольники, в которые вписаны только единичные (для СДНФ) или нулевые (для СКНФ) значения логической функции. Эти квадраты и прямоугольники должны быть образованы соприкасающимися единичными ячейками карты. Целью минимизации является покрытие всех единичных значений логической функции в ячейках карты Карно минимальным количеством квадратов и прямоугольников максимальной площади (количество клеток в фигурах должно быть четным). При этом площадь квадратов и прямоугольников должна быть 2r, где r0…(n – 1), n – количество аргументов логической функции.
fМДНФ(x, y, z) = x ͞y ͞y z. d. Построим многочлен Жегалкина исходной функции, применяя метод неопределенных коэффициентов. Полином Жегалкина для функции от трёх переменных имеет вид: P(x, y, z) = a0 a1x a2y a3z a4xy a5xz a6yz a7xyz, где a0, a1, a2, a3, a4, a5, a6, a7 – неопределенные коэффициенты. Подставляя в выражение значения переменных и функции на конкретных наборах, получаем уравнения для вычисления коэффициентов. P(0,0,0) = 0 = a0 P(0,0,1) = 1 = a0 a3 = 0 a3, a3 = 1 P(0,1,0) = 0 = a0 a2 = 0 a2, a2 = 0 P(0,1,1) = 0 = a0 a2 a3 a6 = 0 0 1 + a6, a6 = 1 P(1,0,0) = 1 = a0 a1 = 0 a1, a1 = 1 P(1,0,1) = 1 = a0 a1 a3 a5 = 0 1 1 a5, a5 = 1 P(1,1,0) = 0 = a0 a1 a2 a4 = 0 1 0 a4, a4 = 1 P(1,1,1) = 0 = a0 a1 a2 a3 a4 a5 a6 a7 = 0 1 0 1 1 1 1 a7 = 1 a7, a7 = 1. Таким образом, полином Жегалкина для данной функции имеет вид: P(x, y, z) = x z xy xz yz xyz. e. Построим таблицу двойственной функции. Пусть f – некоторая булева функция. Тогда двойственной к f (обозначается f*) называют функцию, таблица истинности которой получается из таблицы истинности f заменой всех 0 на 1, а всех 1 на 0. Такую операцию называют инвертированием таблицы истинности. Инвертирование происходит не только со значениями функции, но и со значениями аргументов. Поскольку в таблице истинности записывают значения переменных в лексикографическом порядке, после построения её нужно «перевернуть», то есть переставить все строки в обратном порядке. Тогда таблица значений двойственной функции будет иметь вид:
f. Построим СКНФ двойственной функции по таблице ее значений. СКНФ – конъюнкция элементарных дизъюнкций (макстермов, конституент нуля). В СКНФ входят наборы переменных, на которых значение функции равно 0, причем, если значение переменной равно 0, то она входит в макстерм без отрицания, а если 1 – то с отрицанием. Для данной функции нулевые значения определяются на наборах 010 (2), 011 (3) и 110 (6): f*СКНФ(x, y, z) = (x ͞y z)(x ͞y ͞z)(͞x ͞y z) g. Проверим исходную функцию на принадлежность основным классам замкнутости T0, T1, L, M, S. Так как f(0,0,0) = 0, функция принадлежит к классу T0. Так как f(1,1,1) = 0, функция не принадлежит к классу T1. Так как f(0,0,1) > f(0,1,0), функция не принадлежит к классу М. Так как f(0,0,0) = f(1,1,1), функция не принадлежит к классу S. Так как полином функции P(x, y, z) = x z xy xz yz xyz содержит конъюнкции, функция не принадлежит к классу L. Заполним таблицу Поста:
h. Выразим отрицание h(x) = x и конъюнкцию g(x, y) = xy через функцию f(x, y, z) и ее отрицание. Функция f не принадлежит классу монотонных функций М. Найдем пару наборов, на которой нарушается монотонность, к примеру, набор (001) и (010). h(х) = f(0,х,х) = х, так как h(01) = f(001) = 1; h(10) = f(010) = 0. Таким образом, f(x, y, z) = h(x) = x. Для построения конъюнкции из функции fМДНФ(x, y, z) = x ͞y ͞y z зафиксируем переменную z = 0 и обозначим: x → x, ͞y → y. Тогда f(x, y, 0) = x ͞y ͞y ∙0 = x ͞y = xy = g(x, y). |

 ͞x ͞z
͞x ͞z 1
1 1
1