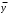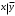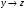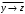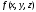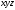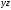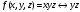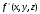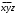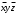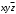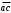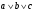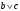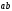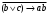логика. Задание2. Решение. Заменим на, на, на, на, на получим формулу логики высказываний
 Скачать 216.24 Kb. Скачать 216.24 Kb.
|
|
Задача1. Доказать равенство множеств 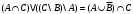 . .Решение. ( 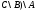 =[ =[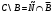 ]= ]=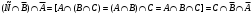 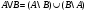 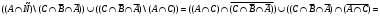 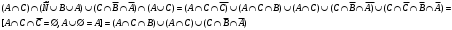 Заменим Заменим 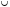 на на  , , 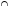 на на  , ,  на на  , ,  на на 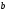 , , на на  получим формулу логики высказываний получим формулу логики высказываний 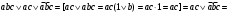 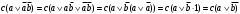 . Сделаем обратную замену и получ . Сделаем обратную замену и получ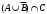 . Таким образом . Таким образом 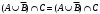 . .Задача2. Построить таблицу истинности для логической функции 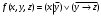 . .Решение. Построим таблицу истинности
Задача3. Найти выражение для функции, двойственной данной 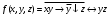 и определить номер двойственной функции. и определить номер двойственной функции.Решение. Преобразуем функцию 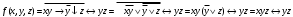 . . Булева функция 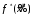 = =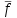 ( (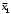 , ,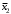 , ,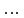 , ,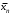 )называется двойственной к функции f( )называется двойственной к функции f(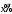 ). ). Заметим, что БФ 0 двойственна к 1, 1 ———————— 0, x ———————— x , 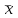 ———————— ———————— 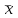 , ,x Ù y ——————— x Ú y, x Ú y ——————— x Ù y. Для формул под множеством 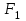 = {0, 1, = {0, 1, 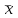 , xy, x Ú y} принцип двойственности можно сформулировать так: для получения формулы, двойственной к формуле А над , xy, x Ú y} принцип двойственности можно сформулировать так: для получения формулы, двойственной к формуле А над 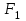 , следует везде в А заменить 0 на 1, 1 на 0, Ù на Ú, Ú на Ù. Например, если А=0× x Ú y× , следует везде в А заменить 0 на 1, 1 на 0, Ù на Ú, Ú на Ù. Например, если А=0× x Ú y×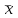 , то , то 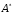 =(1 Ú x) × =(1 Ú x) × × (y Ú 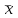 ). ). Заметим, что функция 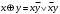 в соответствии с принципом двойственности двойственна функции в соответствии с принципом двойственности двойственна функции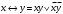 . .Построим двойственную функцию 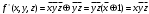 . Ее таблица истинности имеет вид: . Ее таблица истинности имеет вид:
Каждому двоичному набору 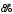 можно сопоставить число можно сопоставить число 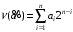 – номер набора – номер набора 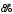 . Значит номер нашей функции . Значит номер нашей функции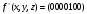 равен равен 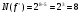 . .Задача4. Упростить выражение для функции 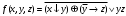 . .Решение. 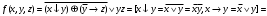 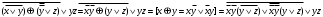 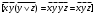 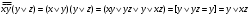 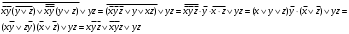 Задача5. Найти СДНФ, СКНФ для функции с заданным номером 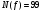 и упростить по методу Квайна СДНФ. и упростить по методу Квайна СДНФ.Решение. 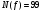 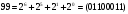 Таблица истинности функции имеет вид
CДНФ 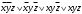 CКНФ 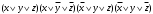 Таблица Квайна
СДНФ является одновременно и Сокращенной , Тупиковой и минимальной ДНФ. Задача 6. Найти полином Жегалкина для функции с заданным номером 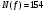 Решение 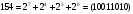 Таблица истинности функции имеет вид
CДНФ 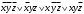 . . Заменим в СДНФ знак дизъюнкции на сумму по модулю два,это возможно, так как в СДНФ на данном наборе может быть равна 1 , только одна конъюнкция,поэтому максимум из одой 1 и остальных нулей равен их сумме по модулю два,получим 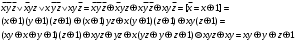 Задание 7. Доказать секвенцию табличным методом. 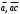 ├ ├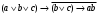 Решение. ФЛВ 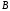 называется логическим следствием ФЛВ называется логическим следствием ФЛВ 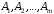 , если для любого набора значений переменных , если для любого набора значений переменных 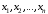 , которые входят в , которые входят в 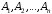 и и 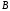 , значение , значение 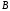 есть 1 всякий раз, когда значение каждой есть 1 всякий раз, когда значение каждой 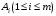 на этом наборе равно 1; в этом случае будем писать: на этом наборе равно 1; в этом случае будем писать: 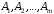 ╞ ╞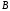 (читается «из (читается «из 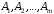 логически следует логически следует 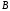 »). »).
Необходимо рассмотреть только те наборы , где обращаются в 1 обе формулы 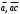
Из таблицы видно , что на этих наборах формула 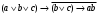 также обращается в1, следовательно она логически следует из посылок. также обращается в1, следовательно она логически следует из посылок.Задание 8. Доказать тавтологию методом резолюций. 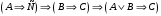 Решение. 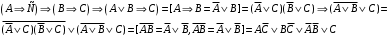 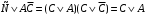 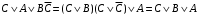 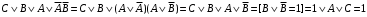 Задание 9. Проанализировать вывод секвеции. 1) 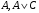 ├ ├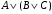 . Формула неверна, такого правила вывода нет. . Формула неверна, такого правила вывода нет.2) 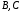 ├ ├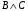 -введение конъюнкции. -введение конъюнкции.3) 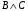 ├ ├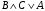 -–введение дизъюнкции -–введение дизъюнкции4) 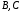 ├ ├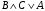 - из 2), 3) по правилу Если из - из 2), 3) по правилу Если из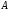 ├ ├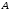 , ,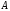 ├ ├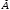 ,то ,то 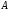 ├ ├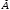 5) 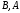 ├ ├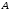 по правилу по правилу 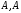 ├ ├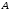 , должно быть правило из , должно быть правило из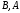 ├ ├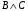 , а иначе фрормула , а иначе фрормула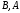 ├ ├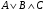 не верна. не верна.6) 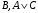 ├ ├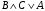 - формула не верна - формула не верна7) 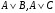 ├ ├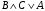 - формула не верна. - формула не верна. |