тест Булевы функции. Тест Булевы функции. Булевы функции Набор, где называется
 Скачать 419 Kb.
|
|
Тест№2 «Булевы функции» Набор  , где  называетсяА) кубом Б) булевым вектором В) булевой функцией Г) булевым кубом Наборы  = и  = называются соседними, если А) они различаются только в одной координате Б) отличаются во всех координатах В) не отличаются Г) отличаются в двух координатах Булевой функцией от n переменных называют А) Набор , где Б) функцию А , принимающую значения 0 и 1В) функцию А , принимающую одно из двух значений 0 или 1Г) функцию А Наборы = и = называются противоположными, если А) они различаются только в одной координате Б) отличаются в двух координатах В) не отличаются Г) отличаются во всех координатах Графический способ задания булевой функции осуществляется с помощью А) таблицы истинности Б) единичного n-мерного куба В) квадрата Г) системы координат Штрих Шеффера читается как А) или не Б) не и В) не или Г) и не «или не» А) штрих Шеффера Б) стрелка Пирса В) отрицание конъюнкции Г) сложение по модулю 2 Обозначение операции Штрих Шеффера А)  Б) x+y В)  Г) (  )Сложение по модулю два означает А) 1+1=2 Б) 1+1=1 В) 1+1=0 Г) 1+0=0 А) штрих Шеффера Б) стрелка Пирса В) отрицание конъюнкции Г) сложение по модулю 2  А) штрих Шеффера Б) отрицание дизъюнкции В) сложение по модулю 2 Г) стрелка Пирса Одночлен от некоторых переменных называется совершенным, если А) они входят в него точно один раз либо со знаком отрицания, либо без него. Б) каждая из этих переменных входит в него либо со знаком отрицания, либо без него. В) каждая из этих переменных входит в него точно один раз либо со знаком отрицания, либо без него. Г) каждая из этих переменных входит в него точно один раз  А) СДНФ Б) СКНФ В) МДНФ Г) ДНФ Чтобы представить ДНФ в виде СДНФ нужно А) каждое слагаемое домножить на 0, а 0 расписать как дизъюнкцию нехватающей переменной и ее отрицания Б) к каждому множителю прибавить 1, а 1 расписать как конъюнкцию нехватающей переменной и ее отрицания В) к каждому множителю прибавить 0, а 0 расписать как конъюнкцию нехватающей переменной и ее отрицания Г) каждое слагаемое домножить на 1, а 1 расписать как дизъюнкцию нехватающей переменной и ее отрицания Чтобы представить КНФ в виде СКНФ нужно А) каждое слагаемое домножить на 1, а 1 расписать как дизъюнкцию нехватающей переменной и ее отрицания Б) к каждому множителю прибавить 1, а 1 расписать как конъюнкцию нехватающей переменной и ее отрицания В) к каждому множителю прибавить 0, а 0 расписать как конъюнкцию нехватающей переменной и ее отрицания Г) к каждому множителю прибавить 0, а 0 расписать как конъюнкцию нехватающей переменной и ее отрицания В таблице истинности СДНФ форме соответствует значение А) 1 Б) 0 В) 0 и 1 Г) 1или 0 Представить ДНФ в виде СДНФ  А)  Б)  В)  Г)  По данной СДНФ записать СКНФ  А)  Б)  В)  Г)  Представить КНФ в виде СКНФ  А)  Б)  В)  Г)  По данной СКНФ записать СДНФ  А)  Б)  В)  Г)  По данной таблице истинности f(0,0,0)=f(0,1,0)=f(1,1,0)=0 построить СКНФ А) Б)  В)  Г)  По данной таблице истинности f(0,0,0)=f(0,1,0)=f(1,1,0)=0 построить СДНФ А) Б) В)  Г)  f(0,0,0)=f(0,1,0)=f(1,1,0)=f(0, 1,1)=1 А) СКНФ Б) КНФ В) СДНФ Г) ДНФ Построить таблицу истинности для  А) f(1,1,1)=f(1,0,1)=f(0,0,1)=f(0,1,1)=f(1,0,0)=f(0,1,0)=1 Б) f(1,1,1)=f(1,0,1)=f(0,0,1)=f(0,1,1)=f(1,0,0)=f(0,1,0)=0 В) f(0,0,0)=f(0,1,0)=f(1,1,0)=f(1,0,0)=f(0,1,1)=f(1,0,1)=1 Г) f(0,0,0)=f(0,1,0)=f(1,1,0)=f(1,0,0)=f(0,1,1)=f(1,0,1)=0 Найти графически минимальную нормальную форму f(a,b,c)=  А  ) f(a,b,c)=b Б  ) f(a,b,c)=  В) f(a,b,c)=  Г ) f(a,b,c)=  Построить минимальную ДНФ по единичному n-мерному кубу  А)  Б)  В)  Г)  Построить минимальную ДНФ по единичному n-мерному кубу  А)  Б)  В)  Г)  Построить СДНФ по единичному n- мерному кубу  А)  Б)  В)  Г)  С помощью карт Карно найти МДНФ 
 Б)
 В)
 Г)
 Построить минимальную ДНФ по единичному n-мерному кубу  А)  Б)  В) Г)  Правильно заполнить карты Карно для f(x,y,z)=  А)
Б)
В)
Г)
Выбрать верное свойство суммы Жигалкина А)  Б)  В)  Г)  Выбрать не свойство суммы Жигалкина А)  Б)  В)  Г)   А)  Б)  В)  Г)  Полином Жигалкина- это А) представление булевой функции с помощью констант, операции конъюнкции и двоичного сложения Б) представление булевой функции с помощью констант, операции дизъюнкции и двоичного сложения В) представление булевой функции с помощью операции дизъюнкции и двоичного сложения Г) представление булевой функции с помощью констант, операции конъюнкции Представить в виде полинома Жигалкина  А)  Б)  В)  Г)  x+x=? А) 1 Б) 0 В) x Г)  x+1=? А) x Б) В) 0 Г) 1 Функция  называется двойственной функцией ,еслиА) = Б) = В) = Г)  = Функция называется самодвойственной, если А) = Б) для любых  следует, что  В) ее полином Жигалкина имеет первую степень Г)  Функция называется линейной, если А) Б) = В) ее полином Жигалкина имеет первую степень Г) для любых следует, что Функция называется монотонной, если А) Б) для любых следует, что В) ее полином Жигалкина имеет первую степень Г) = Полная система называется базисом, если А) вместе с функциями из этого множества она содержит все их суперпозиции Б) удаление хотя бы одной функции превращает эту систему в неполную В) ее полином Жигалкина имеет первую степень Г) для любых следует, что Функция называется шефферовой А) она образует базис Б) вместе с функциями из этого множества она содержит все их суперпозиции В) удаление хотя бы одной функции превращает эту систему в неполную Г) если любая булева функция может быть выражена через функции  с помощью суперпозицийДля того, чтобы система булевых функций была полной необходимо и достаточно, чтобы для каждого из классов Т0, Т1, S,L,M нашлась функция, не принадлежащая этому классу А) важное свойство суммы Жигалкина Б) теорема о замкнутых классах В) теорема Буля Г) теорема Поста Основные замкнутые классы булевых функций А) Т0, Т1, S,K,M Б) Т0, Т , S,L,M В) Т0, Т1, S,L,M Г) Т0, S,L,N, M Система булевых функций называется полной, если А) вместе с функциями из этого множества она содержит все их суперпозиции Б) любая булева функция может быть выражена через функции с помощью суперпозицийВ) удаление хотя бы одной функции превращает эту систему в неполную Г) ее полином Жигалкина имеет первую степень Множество булевых функций называется замкнутым, если А) вместе с функциями из этого множества оно содержит все их суперпозиции Б) его полином Жигалкина имеет первую степень В) любая булева функция может быть выражена через функции с помощью суперпозицийГ) удаление хотя бы одной функции превращает это множество в неполное Определить к какому замкнутому классу относится булева функция А) Т1, S,M Б) Т0, Т1 В) Т1, L,M Г) Т1,M Определить к какому замкнутому классу относится булева функция  А) Т0, Т1 Б) Т1, S,M В) Т1,M Г) Т1, L,M Определить к какому замкнутому классу относится булева функция 0 А) Т0,L,M Б) Т1, S,M В) Т1, S,L Г) Т0,S,M Определить к какому замкнутому классу относится булева функция 1 А) Т1, S,M Б) Т1, L,M В) Т1,M Г) Т1, L,S Определить к какому замкнутому классу относится булева функция x А) Т0, Т1,L,M Б) Т0, S,L,M В) Т0, Т1, S,L,M Г) Т0, Т1, S,L Определить к какому замкнутому классу относится булева функция А) Т0, S Б) Т0, Т1, S В) S,L,M Г) S,L Определить к какому замкнутому классу относится булева функция  А) Т0, Т1, S,L Б) S,L,M В) Т0, Т1,M Г) Т0, Т1, S Определить к какому замкнутому классу относится булева функция  А) Т0, Т1,M Б) Т0, Т1, S,L В) Т0, Т1, S Г) S,L,M Определить к какому замкнутому классу относится булева функция А) S,L,M Б) ни к какому В) Т0, Т1, S,L Г) ко всем Определить к какому замкнутому классу относится булева функция А) ко всем Б) Т0, Т1, S В) Т0, Т1,M Г) ни к какому Определить к какому замкнутому классу относится булева функция x+y А) Т0, L Б) ни к какому В) ко всем Г) S,L,M Выбрать не полную систему А)  Б) 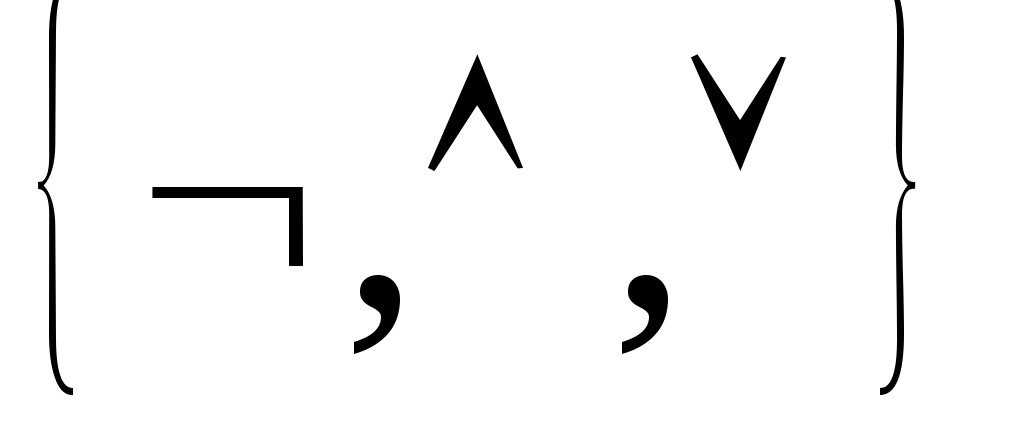 В)  Г)  Выбрать полную систему А) Б)  В)  Г)  Найти двойственную функцию к данной x+y А)  Б)  В)  Г)  Найти двойственную функцию к данной  А)  Б)  В)  Г)   А) 1 Б) 0 В) x Г) Найти двойственную функцию к данной А)  Б)  В)  Г)  Ответы к тесту №2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
