Главная страница
Навигация по странице:

  • Решение Вводим параметры: c= 3 ;d= 1 ; Вводим матрицу X и матрицу вероятностей X: X =[1 2 3]

  • DZ=0; for i=1:3 for j=1:2 DZ=(Z(i,j)-MZ)^2*pZ(i,j); end ; end ; DZ

  • Решение Вводим данные: c =5; d =10; Вычисляем параметр a: a =(1-0.32-0.41-0.05)/3

  • X=[-10 -5 0 c d] X =-10 -5 0 5 10 pX=[a 0.32 2*a 0.41 0.05]

  • MX=X*pX. MX =0.2167 DX=(X.*X)*pX.-MX*MX DX =30.5364 SX=sqrt(DX)

  • Решение Исходные данные: MX =8; MY =7; DX =9; DY =6;

    		•

    Математические основы теории систем 1. Контрольная_0. Решение Вводим параметры c3d1 Вводим матрицу x и матрицу вероятностей X X1 2 3 x


    Скачать 22.25 Kb.
    НазваниеРешение Вводим параметры c3d1 Вводим матрицу x и матрицу вероятностей X X1 2 3 x
    АнкорМатематические основы теории систем 1
    Дата12.01.2023
    Размер22.25 Kb.
    Формат файлаdocx
    Имя файлаКонтрольная_0.docx
    ТипРешение
    #882878

    1. Дано

    X
    1
    2
    3

    p
    1/3
    1/3
    1/3

    Неч. c=3 d=1.

    Чёт c=2 d=2.

    Y
    1
    2

    p
    c/4
    d/4

    Найти M (XY)?

    Решение

    Вводим параметры:

    c=3;d=1;

    Вводим матрицу X и матрицу вероятностей X:

    X=[1 2 3]
    X =

    1 2 3
    pX=[1/3 1/3 1/3]
    pX =

    0.3333 0.3333 0.3333
    Вводим матрицу Y и матрицу вероятностей Y:

    Y=[1 2]
    Y =

    1 2
    pY=[c/4 d/4]
    pY =

    0.7500 0.2500
    Матрица произведения:

    Z=X.'*Y
    Z =

    1 2

    2 4

    3 6
    Матрица вероятностей произведения:

    pZ=pX.'*pY
    pZ =

    0.2500 0.0833

    0.2500 0.0833

    0.2500 0.0833
    Вычисляем математическое ожидание произведения:

    MZ=0;

    for i=1:3

    for j=1:2

    MZ=MZ+Z(i,j)*pZ(i,j);

    end;

    end;
    MZ
    MZ =

    2.5000
    Заодно можно вычислить и дисперсию:

    DZ=0;

    for i=1:3

    for j=1:2

    DZ=(Z(i,j)-MZ)^2*pZ(i,j);

    end;

    end;
    DZ
    DZ =

    1.0208
    2. Дискретная случайная величина имеет следующий ряд распределения:

    Х
    -10
    -5
    0
    c
    d

    р
    а
    0,32
    2a
    0,41
    0,05

    Найти величину a, математическое ожидание и среднее квадратическое отклонение этой случайной величины.

    Неч. c=5 d=10.

    Чёт c=10 d=5.

    Решение_Вводим_данные:_c_=5;_d_=10;_Вычисляем_параметр_a:_a_=(1-0.32-0.41-0.05)/3'>Решение

    Вводим данные:

    c=5;d=10;

    Вычисляем параметр a:

    a=(1-0.32-0.41-0.05)/3
    a =

    0.0733
    Определяем ряд распределения:

    X=[-10 -5 0 c d]
    X =

    -10 -5 0 5 10
    pX=[a 0.32 2*a 0.41 0.05]
    pX =

    0.0733 0.3200 0.1467 0.4100 0.0500
    Вычисляем математическое ожидание, дисперсию и среднее квадратичное отклонение:

    MX=X*pX.'
    MX =

    0.2167
    DX=(X.*X)*pX.'-MX*MX
    DX =

    30.5364
    SX=sqrt(DX)
    SX =

    5.5260
    3. Известны математические ожидания и дисперсии двух независимых случайных величин X и Y: M(X)=8, M(Y)=7, D(X)=9, D(Y)=6. Найти математическое ожидание и дисперсию случайное величины 

    Нечёт: Z=10X-7Y+6.

    Чёт: Z=15X-3Y+4.

    Решение

    Исходные данные:

    MX=8;MY=7;DX=9;DY=6;

    Основные свойства математического ожидания и дисперсии: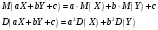



    a=10;b=-7;c=6;

    Вычисляем:

    MZ=a*MX+b*MY+c
    MZ =

    37
    DZ=a^2*DX+b^2*DY
    DZ =

    1194

    написать администратору сайта