механика. РГР№2_Тузова А.Д._АП22. Решение y 0 Ra74148370 Ra111 кн часть i находим продольные силы методом сечений 1 участок
 Скачать 461.17 Kb. Скачать 461.17 Kb.
|
|
В 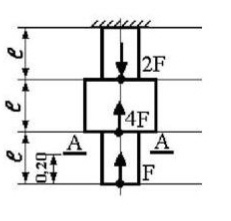 ариант 21 ариант 21Решение: 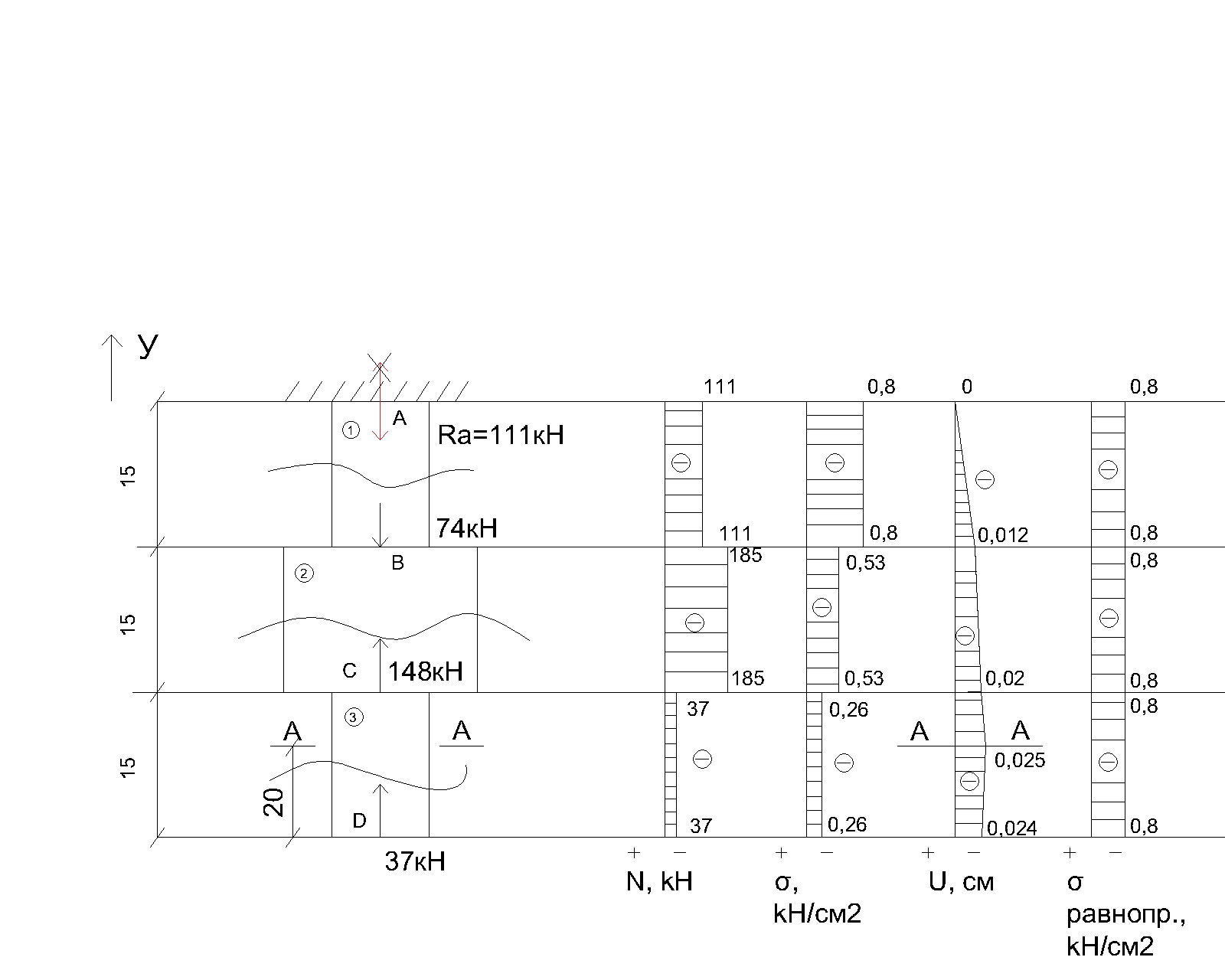 ∑y = 0 Ra-74+148+37=0 Ra=-111 КН ЧАСТЬ I Находим продольные силы методом сечений 1 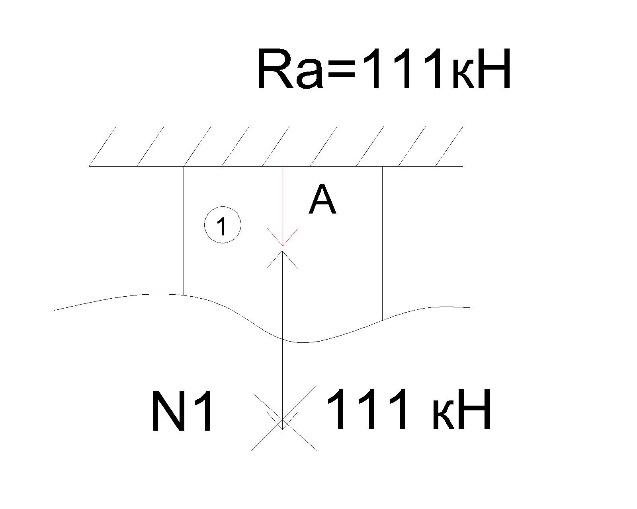 участок участок ∑у =0 -111-N1=0 N1=-111 kH 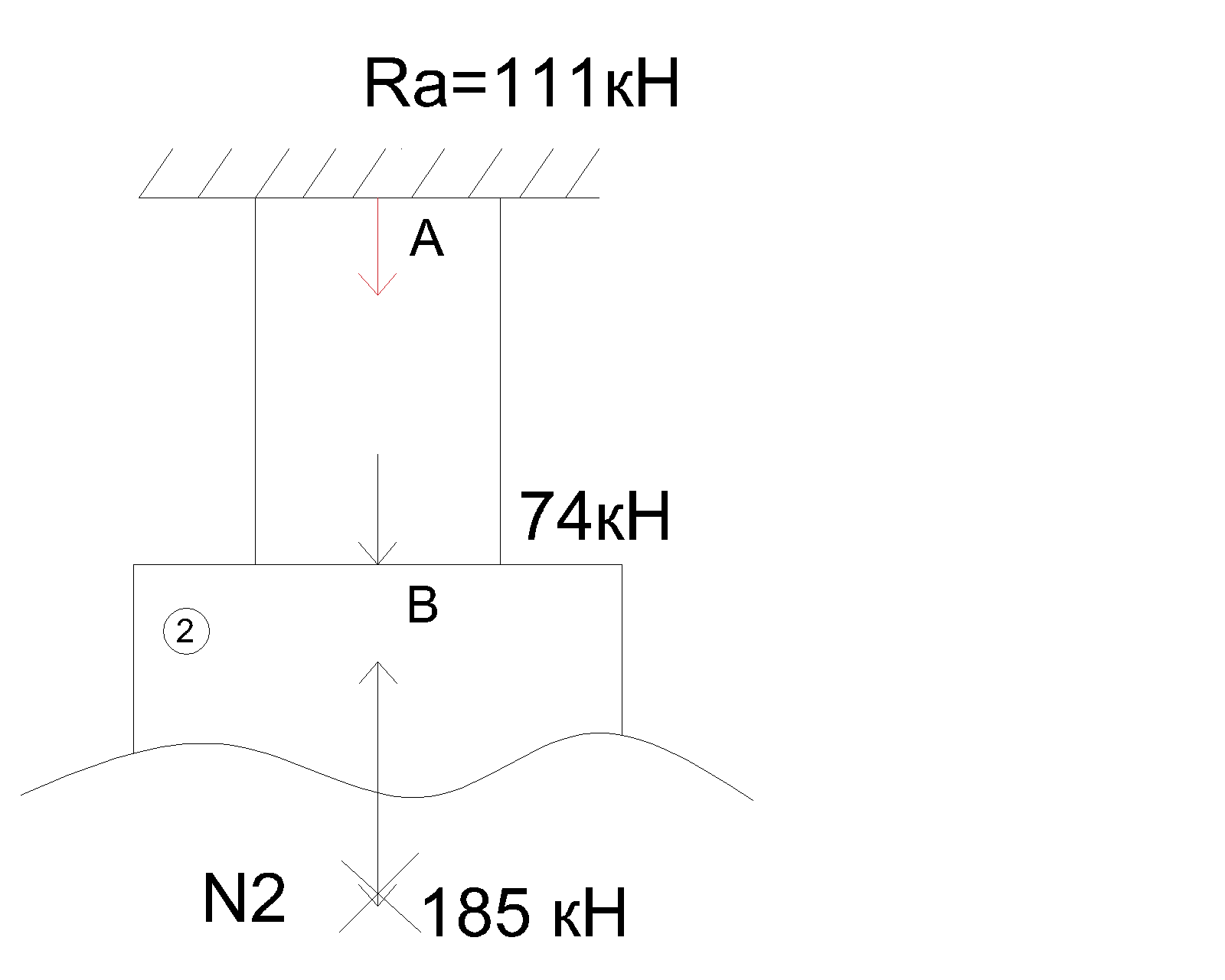 2 участок ∑у =0 -111-74-N2 =0 N2=-185 kH 3 участок 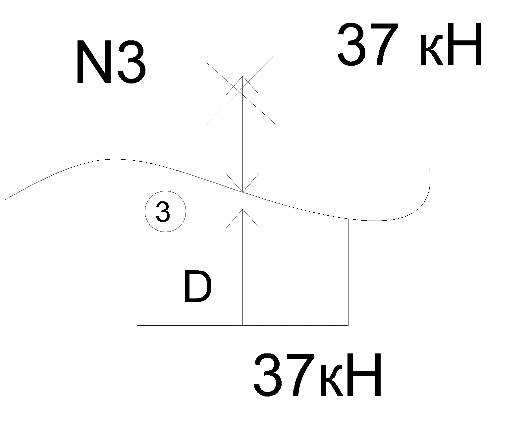 ∑у =0 ∑у =0 N3+37=0 N3=-37 kH Из условия прочности по нормальным напряжениям подбираем площадь поперечного сечения. [σ]=8 MПа =0,8 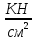 σ = 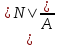 ≤ [σ] => A ≥ ≤ [σ] => A ≥ 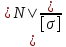 => A ≥ => A ≥ 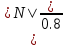 1 участок: A ≥ 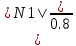 = = 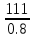 = 138,75 = 138,75 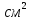 Принять: Принять:2 участок: 2,5A ≥ 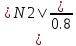 = = 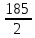 = 92,5 = 92,5 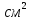 А=138,75 А=138,75 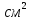 3 участок: A ≥ 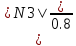 = = 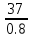 = 46,25 = 46,25 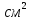 2,5А=346,875 2,5А=346,875 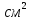 Построить эпюру нормальных напряжений. σ1 = 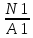 = = 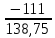 = -0,8 = -0,8 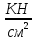 σ2 = 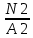 = = 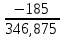 = -0,53 = -0,53 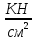 σ3 = 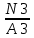 = = 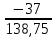 = -0,26 = -0,26 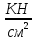 Определить продольную деформацию каждого участка и построить график перемещений поперечных сечений, приняв модуль упругости материала стержня Е = 10 Гпа = 1000 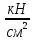 Uа = 0 Ub = Ua + Δ 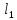 = 0 + = 0 + 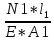 = = 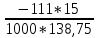 = -0,012 см = -0,012 смUc = Ub + Δ 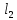 = -0.0093 + = -0.0093 + 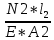 = = 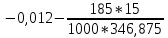 =-0,012 -0,008 = -0,02 см =-0,012 -0,008 = -0,02 смUd = Uc+ Δ 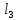 = -0,02 + = -0,02 + 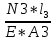 = = 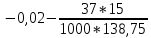 =-0,02-0,004= -0,024 см =-0,02-0,004= -0,024 смUA-A = Ud + Δ 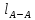 = -0,02 + = -0,02 + 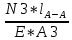 = = 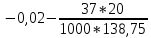 = -0,025 см = -0,025 см5. Определить общий объем ступенчатого стержня. V = 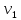 + + 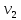 + +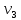 = A1* = A1*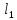 + A2* + A2*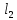 + A3* + A3*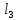 = l(A1+A2+A3)=15(А+2,5А+А) → = l(A1+A2+A3)=15(А+2,5А+А) →V = 15*624,375 = 9365,625 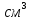 ЧАСТЬ II 1. Подобрать поперечные сечения из условия экономии материала, т.е. максимально уменьшив площадь поперечных сечений, сделав стержень равнонапряженным. [σ]=8 MПа =0,8 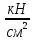 σ = 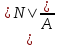 ≤ [σ] => A ≥ ≤ [σ] => A ≥ 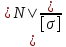 => A ≥ => A ≥ 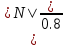 1 участок : : A1 ≥ 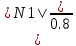 = = 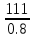 = 138,75 = 138,75 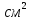 2 участок : : A2 ≥ 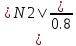 = = 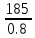 = 231,25 = 231,25 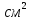 3 участок : : A3 ≥ 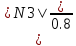 = = 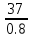 = 46,25 = 46,25 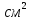 σ1 = 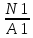 = = 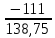 = -0,8 = -0,8 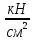 σ2 = 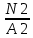 = = 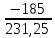 = -0,8 = -0,8 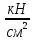 σ3 = 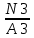 = = 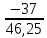 = - 0,8 = - 0,8 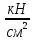 2. Повторно определить продольную деформацию каждого участка и построить новый график перемещений поперечных сечений, приняв тот же модуль упругости Е = 10∙Гпа = 1000 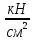 Ua = 0 Ub = Ua + Δ 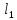 = 0 + = 0 + 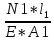 = = 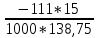 = -0,012 см = -0,012 смUc = Ub + Δ 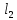 = -0,012+ = -0,012+ 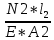 =-0,012- =-0,012- 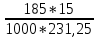 = -0,024 см = -0,024 смUd = Uc + Δ 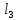 = -0,024 - = -0,024 - 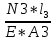 =-0,024- =-0,024- 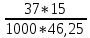 =-0,036 см =-0,036 см3. Определить новый объем стержня и процент экономии материала. Vp = 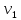 + + 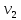 + +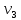 = A1* = A1*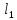 + A2* + A2*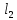 + A3* + A3*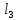 = l(A1+A2+A3) = l(A1+A2+A3)Vp = 15(138,75+231,25+46,25)=15*416,25=6243,75 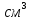 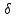 = = 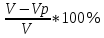 = = 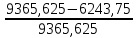 * 100% = 33% * 100% = 33%ЧАСТЬ III 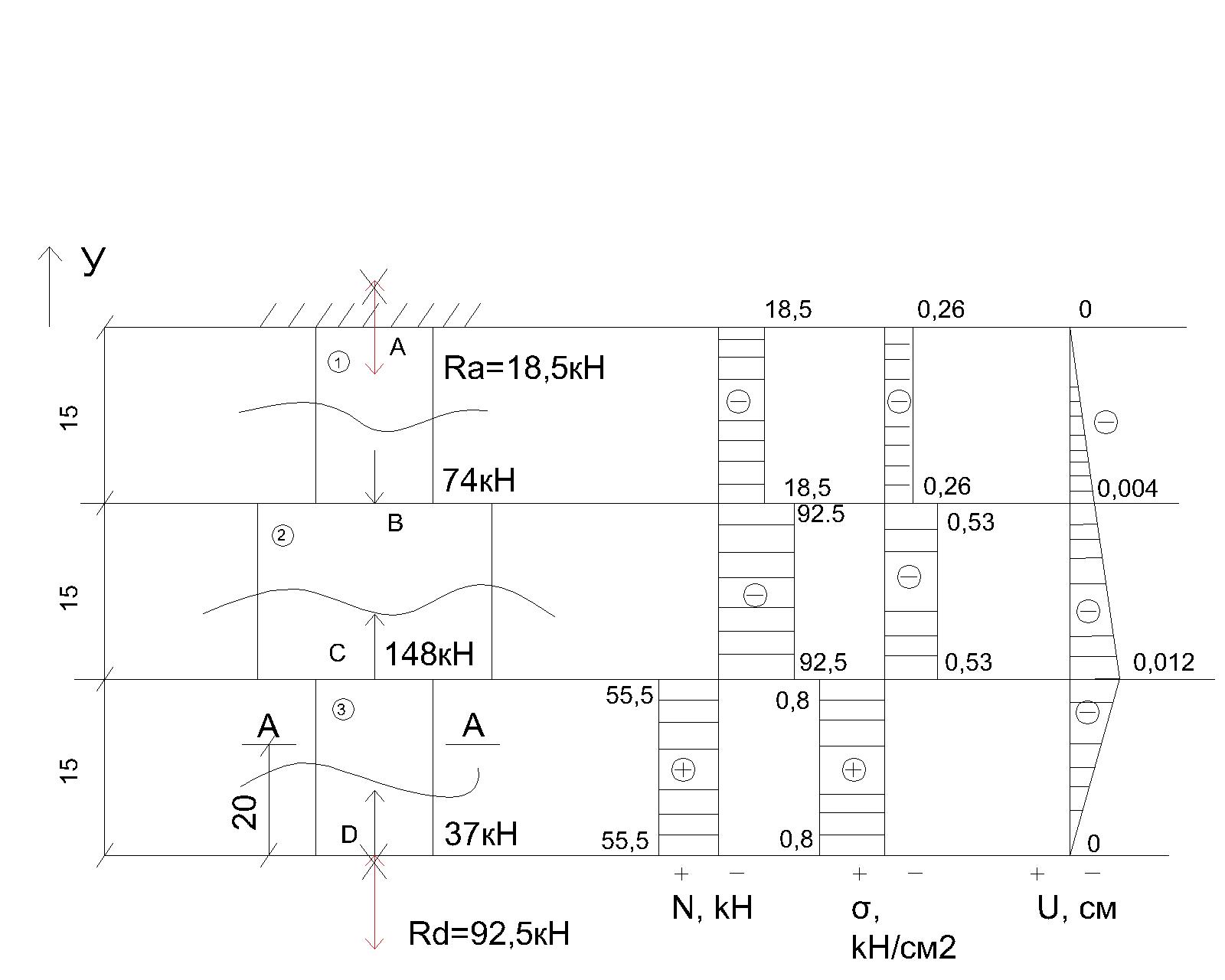 1. Приняв абсолютную деформацию всего ступенчатого стержня раной нулю, определить продольные силы и построить эпюру продольных сил. 1. Приняв абсолютную деформацию всего ступенчатого стержня раной нулю, определить продольные силы и построить эпюру продольных сил.∑y = 0 Ra-74+148+37Rd=0 Ra+Rd=-111 kH (1) Ud=0 Ud = Ua + Δ 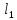 + Δ + Δ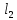 + Δ + Δ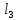 = 0 = 0 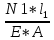 + +  + + 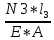 = 0 = 02,5*N1+N2 + 2,5N3 =0 (2) 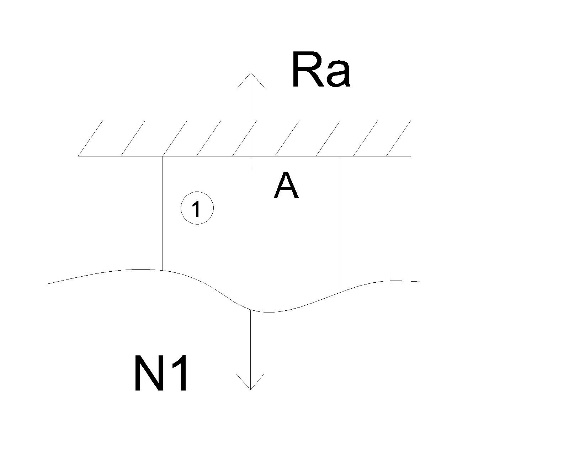 1 участок: 1 участок: ∑у =0 Ra-N1=0 N1=Ra kH (3) 2 участок: 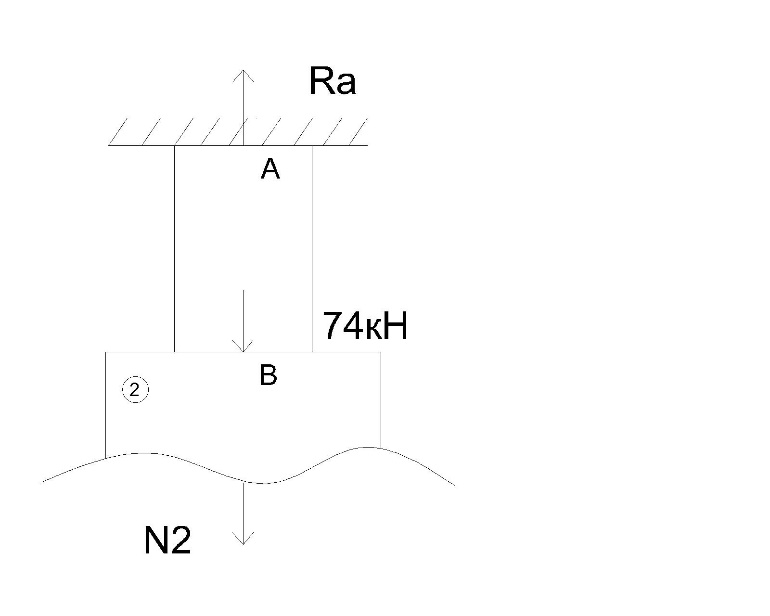 ∑у =0 ∑у =0Ra-74-N2=0 N2=Ra-74 kH (4) 3 участок: 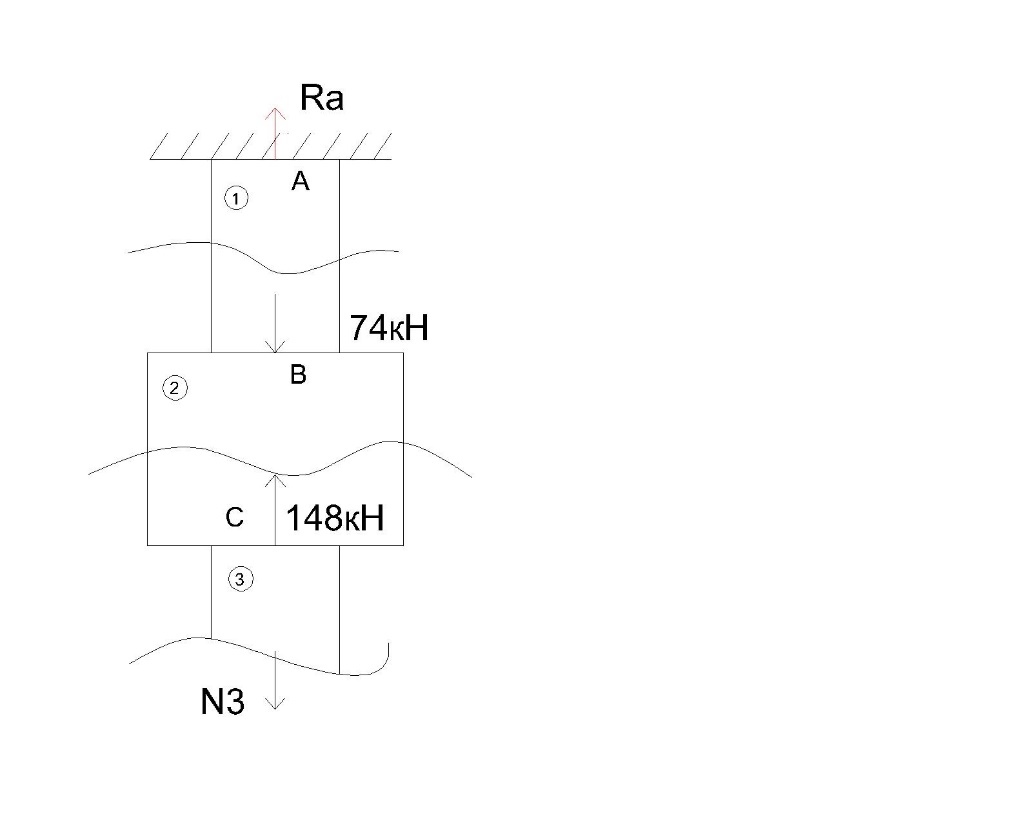 ∑у =0 Ra-37+148N3=0 N3=Ra+74 kH (5) Подставим (3), (4), (5) формулы → во (2). 2,5Ra+Ra-74+2,5(Ra+74)=0 6Ra+111=0 Ra=-18,5 (6) Ra+Rd=-111 -18,5+Rd=-111 Rd=-111+18,5 Rd=-92,5 Подставим (3),(4),(5) в (6) формулу N1=Ra=-18,5 N2=Ra-74=-18,5-74=-92,5 N3= Ra+74=-18,5=74=55,5 2. Из условия прочности по нормальным напряжениям подобрать площадь поперечного сечения для каждой ступени, приняв допускаемое напряжение [σ] =8 МПа и заданное соотношение площадей А1/А2. [σ]=8 MПа =0,8 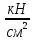 σ = 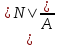 ≤ [σ] => A ≥ ≤ [σ] => A ≥ 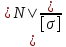 => A ≥ => A ≥ 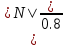 1 участок : A ≥ 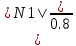 = = 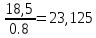 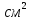 2 участок : 2,5A ≥ 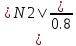 = = 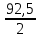 = 46,25 = 46,25 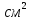 3 участок : A ≥ 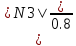 = = 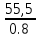 = 69,37 = 69,37 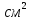 Принимаем А=69,37 см² , 2,5A=173,425 см² 3. Построить эпюру нормальных напряжений. σ1 = 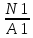 = = 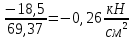 σ2 = 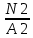 = = 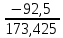 = -0,53 = -0,53 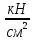 σ3 = 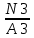 = = 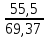 = 0,8 = 0,8 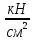 4. Определить продольную деформацию каждого участка и построить график перемещений поперечных сечений, приняв модуль упругости материала стержня Е = 10 ГПа. Ua = 0 Ub = Ua + Δ 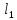 = 0 + = 0 + 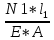 = = = = 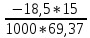 = -0,004 см = -0,004 смUc = Ub + Δ 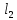 = -0,004 + = -0,004 + 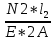 =-0,004- =-0,004- 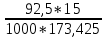 = -0,004-0,008=-0,012 см = -0,004-0,008=-0,012 смUd = Uc + Δ 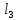 = -0,012 + = -0,012 + 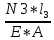 =-0,012+ =-0,012+ 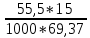 = -0,012+0,012=0 см. = -0,012+0,012=0 см.АП22_Тузова А.Д._РГР №2 |
