Математический бильярд. Решение задач на переливание с помощью метода математического бильярда
 Скачать 101.37 Kb. Скачать 101.37 Kb.
|
|
Решение задач на переливание с помощью метода математического бильярда Введение В век скоростей и нехватки времени люди начинают искать возможности для совмещения нескольких видов деятельности. Игра в бильярд позволяет совместить занятия спортом, общение и отдых. Бильярд - редкостная игра, дозволяющая усовершенствовать физические и умственные способности человека, помогает научиться быть хозяином своих эмоций, добиваться назначенных целей, с честью вести поединок. Впервые о математическом базисе бильярдной игры заговорил известный физик Гаспар Густав Кориолис в своей книге "Математическая теория явлений бильярдной игры" 1835-го года. Прошло более полутораста лет и математический бильярд по сути превратился в огромное дерево с тьмой отростков и гигантских ветвей. "Теория биллиардов" сегодня имеет важнейшее применение в физике. Поэтому целью данной работы является исследование теории математического бильярда и его применении при решении задач на переливание История возникновения бильярда.Игра в шары – одна из первых игр, о которых имеются исторические сведения. Многие исследователи считают, что именно игры в шары, родиной которых стала Азия, стали основой для появления бильярда. Считается, что китайские купцы завезли простенькую игру в шары в Англию, в период средних веков. И уже англичане, усовершенствовав ее – стали родоначальниками бильярда. В Европе первые упоминание о нем имеется в английских летописях VI века. В Россию бильярд был завезен из Голландии Петром I. и быстро завоевал популярность. Подобно тому, как азартная игра в кости вызвала к жизни "исчисление" вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Методы решения логических задач на переливание Решать логические задачи очень увлекательно. Половина решения любой логической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами. Есть люди, для которых решение логической задачи – увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу он приходит необычайно быстро. Замечательно, что при этом он и не могут объяснить, как они пришли к решению. «Ну, это же очевидно, ясно», – говорят они. «Ведь если ...» – и они начинают легко распутывать клубок противоречивых высказываний. «Действительно, все ясно», – говорит слушатель, огорченный тем, что он сам не увидел очевидного рассуждения. Согласитесь, что такое же ощущение часто возникает при чтении детективов. Логические задачи можно решать разными способами. Способы разнообразны и каждый из них имеет свою область применения. Для решения задач на переливания чаще всего используются следующие способы решения: Метод рассуждений; Метод таблиц; Метод блок-схем; Метод бильярда. Метод бильярда. Суть метода заключается в представлении последовательности переливаний аналогично движению бильярдного шарика по столу особой конструкции с размерами, соответствующими объемам первоначально пустых сосудов. Нарисовав на клетчатой бумаге исходную конфигурацию, необходимо проследить возможные движения шарика в соответствии с законом «угол падения равен углу отражения» и попадание им в требуемые точки по условию задачи. Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма. Задачи на получение некоторого количества жидкости из большого или бесконечного по объему сосуда, водоема или источника с помощью двух пустых сосудов В данном разделе рассматриваются задачи, в которых вместо одного из сосудов присутствует бесконечный или большой источник, водоем, из которого можно набирать жидкость любое количество раз, а также сливать жидкость в него. Рассмотрим задачу: как с помощью сосудов объемом 7 и 11 литров и бочкой с водой отмерить 2 литра воды. 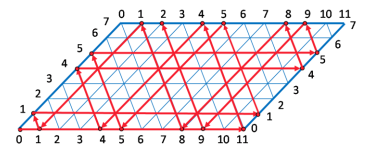 Как ни странно, но головоломки на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов ромбического стола. Границы таких столов удобнее всего рисовать на бумаге, на которую нанесена сетка из одинаковых равносторонних треугольников. В рассматриваемой задаче стороны стола должны иметь длины 7 и 11 единиц. 11 литров 11 4 4 0 11 8 8 1 1 0 11 5 5 0 11 9 9 2 7 литров 0 7 0 4 4 7 0 7 0 1 1 7 0 5 5 7 0 7 По горизонтали отложено количество воды в 11-литровом сосуде в любой момент времени, а по вертикали – та же величина для 7-литрового сосуда. Как же пользоваться диаграммой? Представьте себе, что шар находится в левой нижней вершине в точке 0. Он будет перемещаться вдоль нижнего основания ромба до тех пор, пока не достигнет правой боковой стороны в точке 11. Это означает, что 11-литровый сосуд наполнен до краев, а 7-литровый пуст. Отразившись упруго от правого борта, шар покатится вверх и влево и ударится о верхний борт в точке с координатами 4 по горизонтали и 7 по вертикали. Это означает, что в 11-литровом сосуде осталось всего 4 литра воды, а 7 литров из него перелили в меньший сосуд. Прослеживая дальнейший путь шара и записывая все этапы его движения до тех пор, пока он не попадет в точку 2 верхнего борта, вы получите ответ и узнаете, в какой последовательности необходимо производить переливания, чтобы отмерить 2 литра воды. Все 18 переливаний изображены схематически. Наклонные стрелки говорят о том, что вода переливается из одного сосуда в другой, а вертикальные означают, что либо вода целиком выливается из меньшего сосуда обратно в бочку, либо больший сосуд надо наполнить водой до краев. Является ли это решение самым коротким? Нет,существует второй путь, когда воду сначала наливают в 7-литровый сосуд. Нарисовав траекторию бильярдного шара, читатель убедится в том, что точка 2 достигается на этот раз за 14 отражений от борта. Полученное решение с 14 переливаниями уже является самым коротким. Задачи на переливание сосудов конечного объема Задача. Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды? В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников. Главная диагональ параллелограмма разделена на 8 равных частей, относится к 8-литровому сосуду. 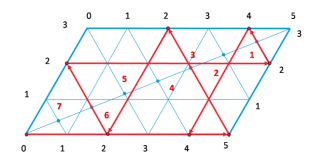 Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд. Прослеживая дальнейший путь шара, и записывая все этапы его движения в виде отдельной таблицы, в конце концов, мы попадаем в точку, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице. 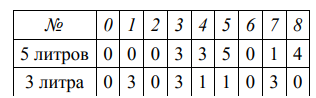 Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким. 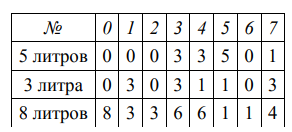 Заключение Для выяснения того, является ли применение метода математического бильярда к решению задач на переливание универсальным способом решения задач данного класса, нами были рассмотрены различные способы решения логических задач на переливание. При рассмотрении способов решения задач на переливание установлено, что все задачи имеют как минимум два способа решения, одно из которых всегда более рационально, но для того, чтобы установить, какое, надо рассмотреть разные варианты решений. В работе подробно рассмотрено применение «Метода бильярда» к решению задач на переливание. Приведены модели таких задач, условия разрешимости и алгоритмы решения с помощью рассматриваемой модели. Выяснено, что данный подход позволяет быстро оценить, все ли объемы можно получить, т.е. во всех ли точках бильярдного стола мы сможем оказаться или же получение каких-то объемов невозможно. Этот метод дает единообразный и систематический подход к решению задач на переливания. Задачи для контроля Две группы туристов готовятся к походу. Для приготовления еды они используют примусы, которые заправляют бензином. В лагере имеется 10- литровая канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить бензин в два сосуда по 5 литров в каждом? Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9- литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров? Как с помощью двух бидонов емкостью 17 литров и 5 литров отлить из молочной цистерны 13 литров молока? Домашнее задание На другой год Вини-Пух запасся 10 литрами меда. Под руками у него два ведра – 7-литровое и 4-литровое. Как ему разделить мед пополам? Для разведения картофельного пюре быстрого приготовления «Зеленый великан» требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана. |
