кочергин. Кочергин_ИИС_пз5. Решение задач управления и наблюдения методами нечеткой логики Цель работы
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
Практическое задание №5 по дисциплине «Интеллектуальные информационные системы» 
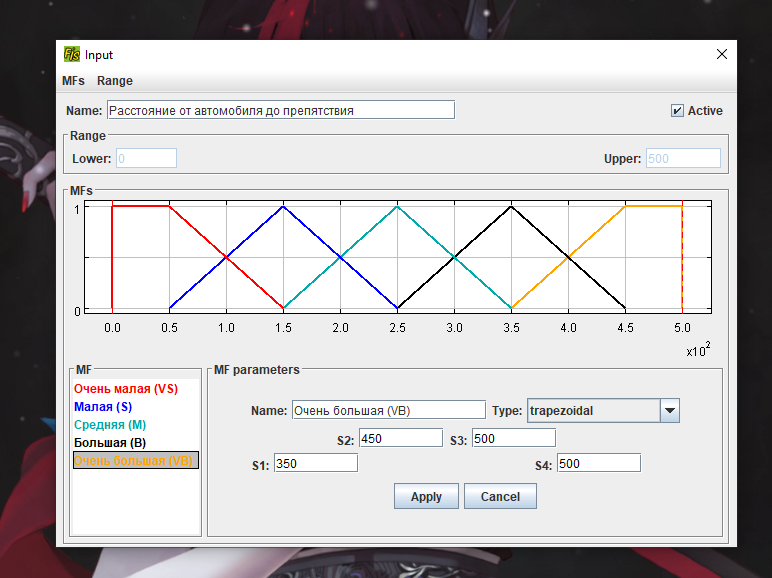
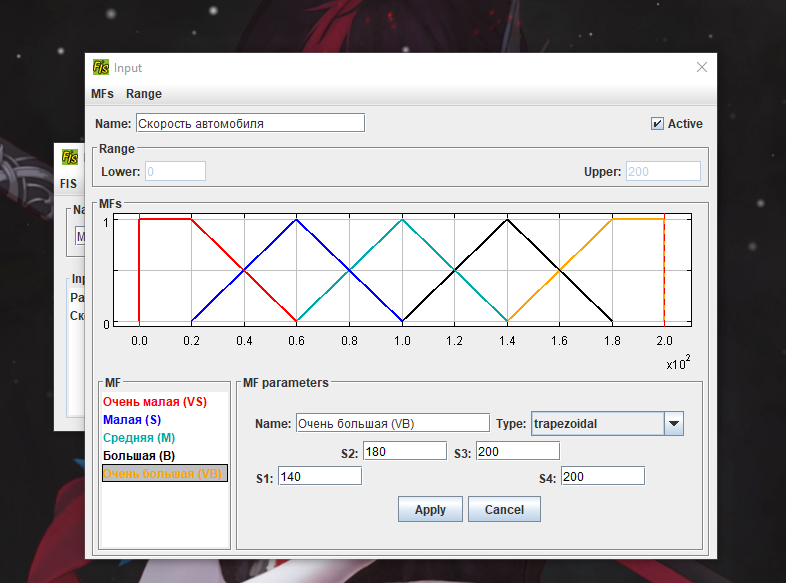
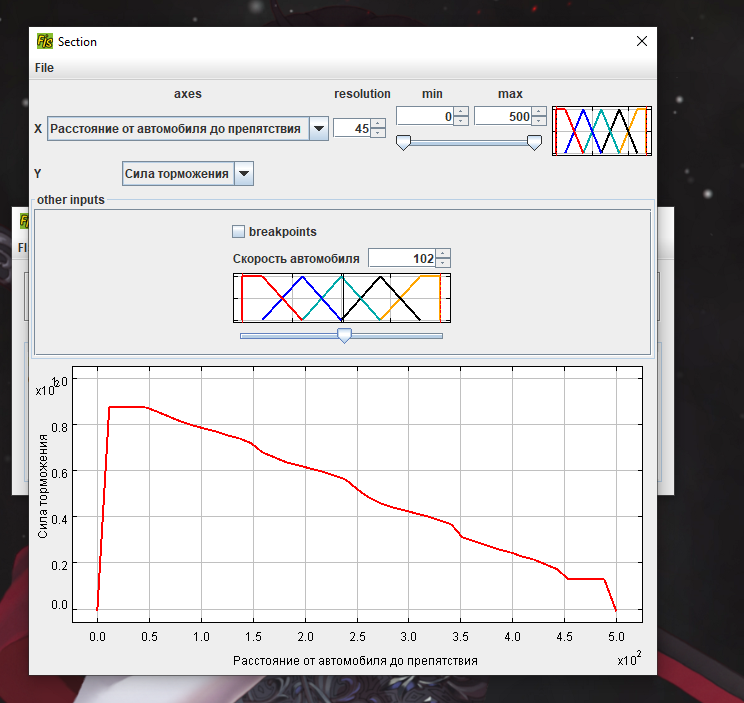
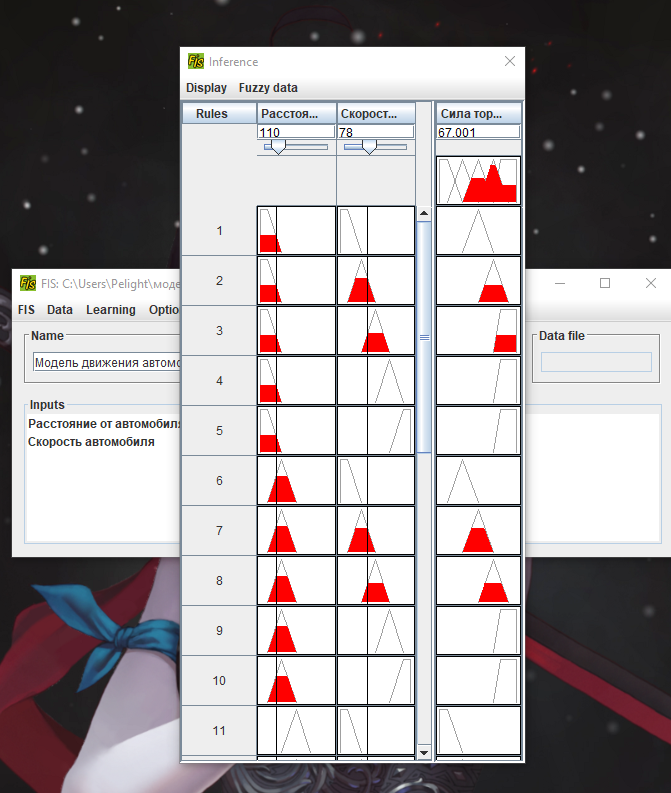
Москва 2022 Лабораторная работа 5 рЕШЕНИЕ ЗАДАЧ УПРАВЛЕНИЯ и наблюдения методами нечеткой логики Цель работы Целью лабораторной работы является ознакомление с инструментальным средством FisPro, а также изучение основ проектирования нечетких систем управления с помощью данного программного средства. 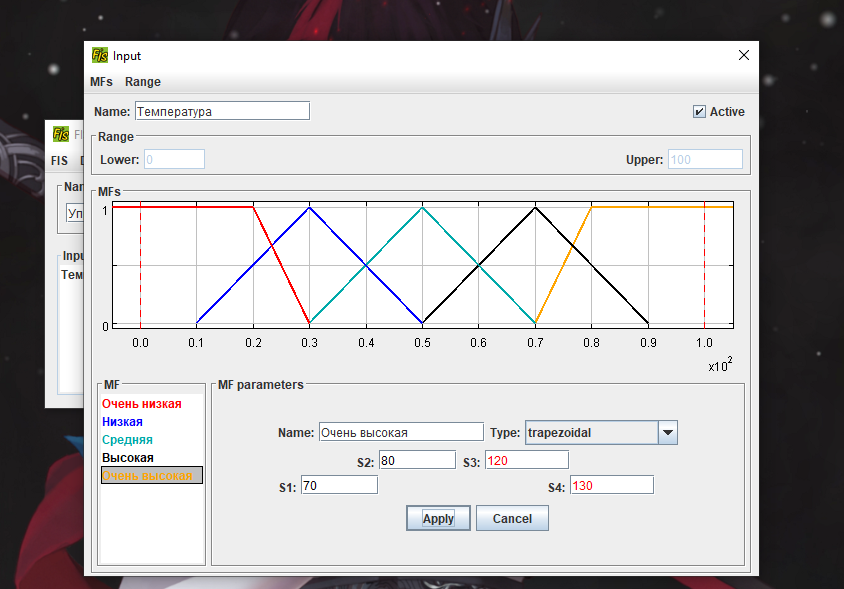 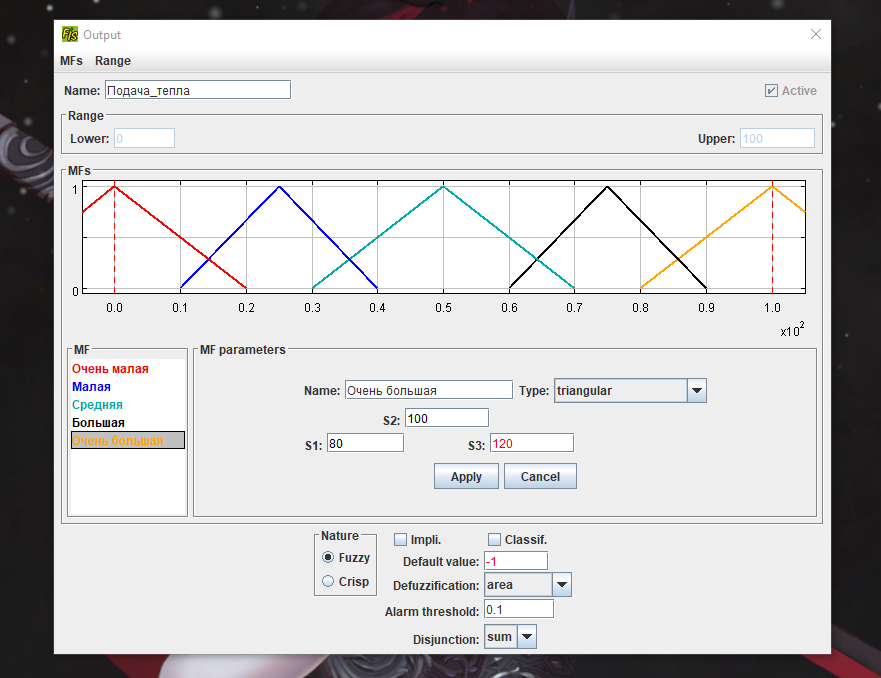 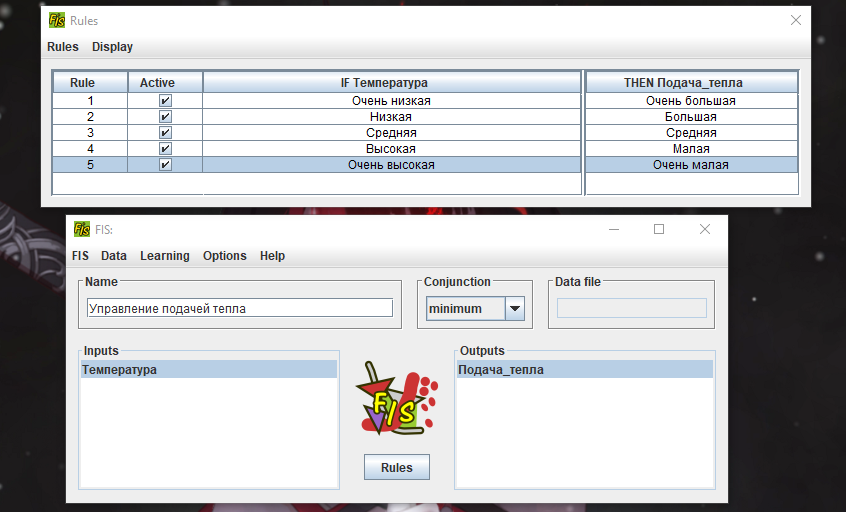 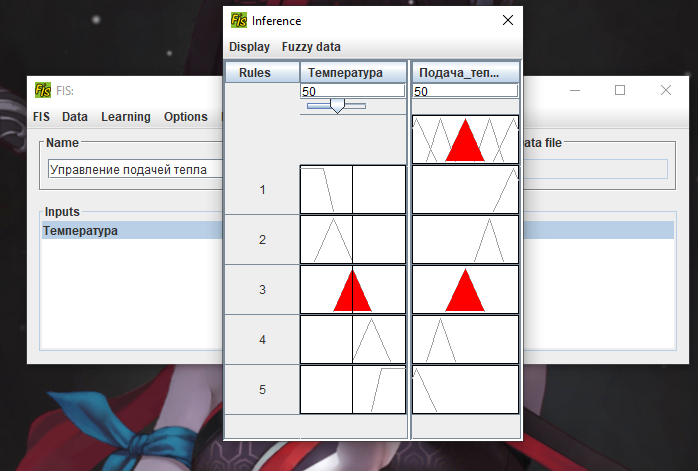 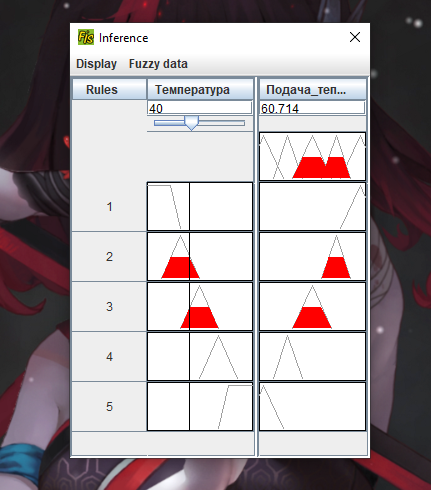 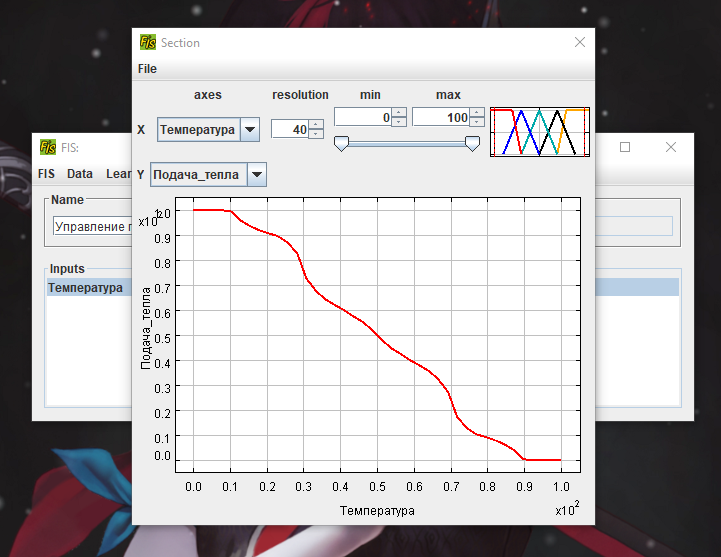 4. Задания к лабораторной работе4.1 Создать модель движения автомобиля по трассе. Входные величины: расстояние от автомобиля до препятствия (изменяется в пределах от 0 до 500), скорость автомобиля (0 - 200). Выходная величина: Сила торможения (0 - 100). Термы для лингвистических переменных расстояние и скорость: очень_мало (VS), мало (S), средне (M), велико (B), очень_велико (VB). Для лингвистической переменной сила_торможения задать следующие термы: близка_к_нулю (Z), четверть (OQ), половина (H), три_четверти (TQ), полная (FU). Выбор формы функции принадлежности и диапазон изменения термов осуществляется аналогично случаю с одной входной переменной. Исходные данные для моделирования представлены в табл. 1.4 – 1.7: Таблица 1.4 Переменная “Скорость”
Таблица 1.5 Переменная “Расстояние”
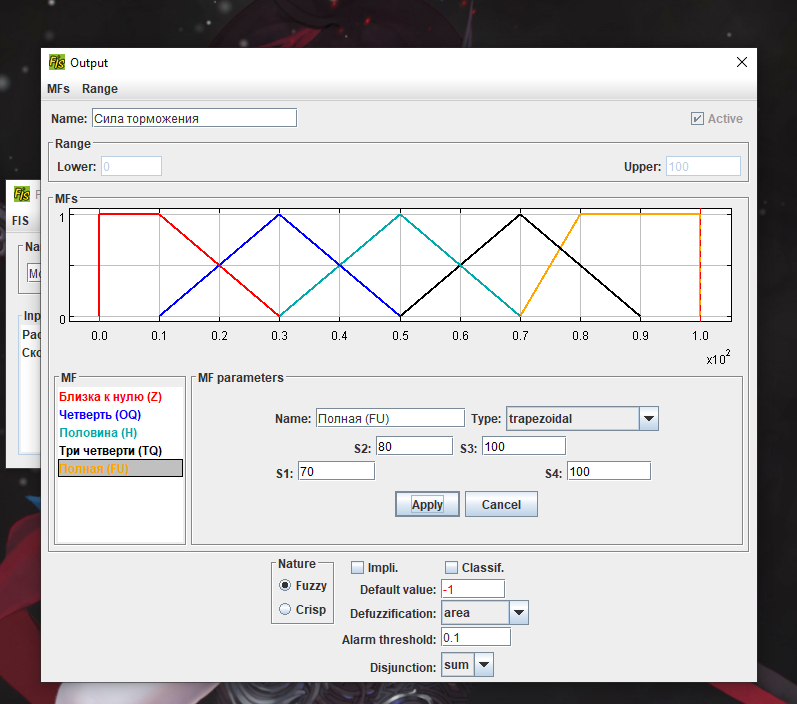
Таблица 1.6 Переменная “Сила торможения”
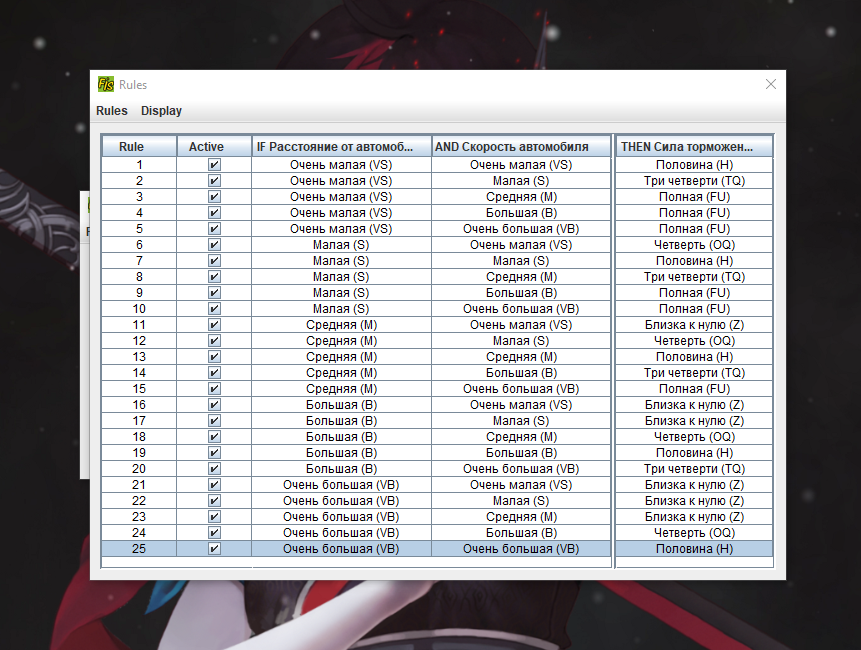
Таблица 1.7 База правил для задачи управления силой торможения автомобиля Скорость
      4.2. Создать нечеткую модель контроля уровня воды в баке Постановка задачи: имеется объект управления в виде бака с водой, к которому подходят две трубы: через одну трубу, снабженную краном, вода втекает в бак, через другую – вытекает. Подачу воды в бак можно регулировать, больше или меньше открывая кран. Контролировать уровень воды в баке можно, например, на основе следующих правил: 1) ЕСЛИ уровень соответствует заданному ТО кран без изменения 2) ЕСЛИ уровень низкий ТО кран быстро открыть 3) ЕСЛИ уровень высокий ТО кран быстро закрыть 4) ЕСЛИ уровень соответствует заданному И его прирост положительный ТО кран медленно закрывать. 5) ЕСЛИ уровень соответствует заданному И его прирост отрицательный ТО кран медленно открывать. 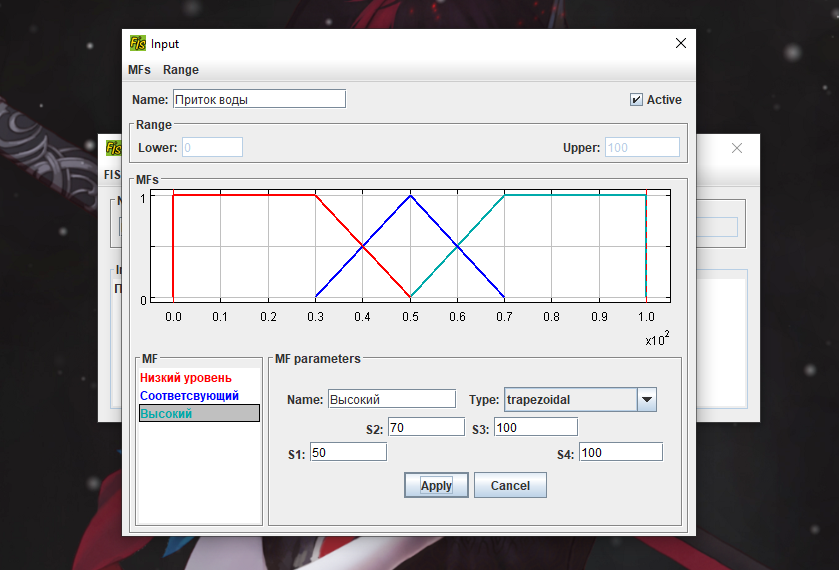 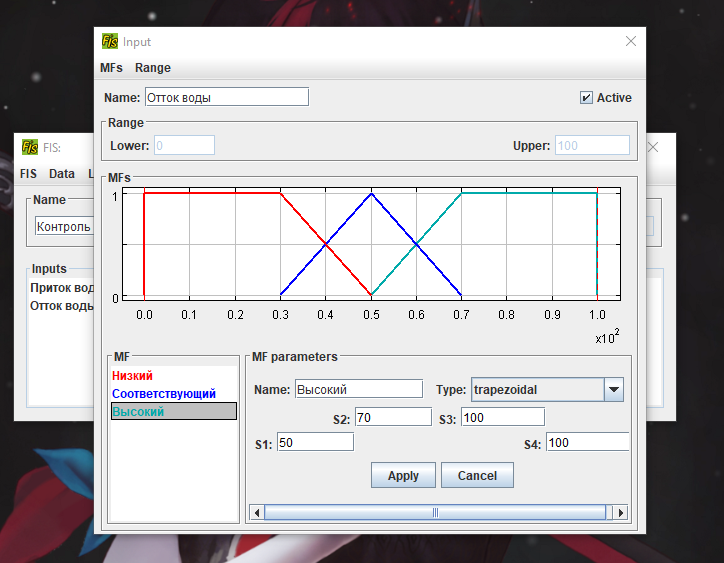 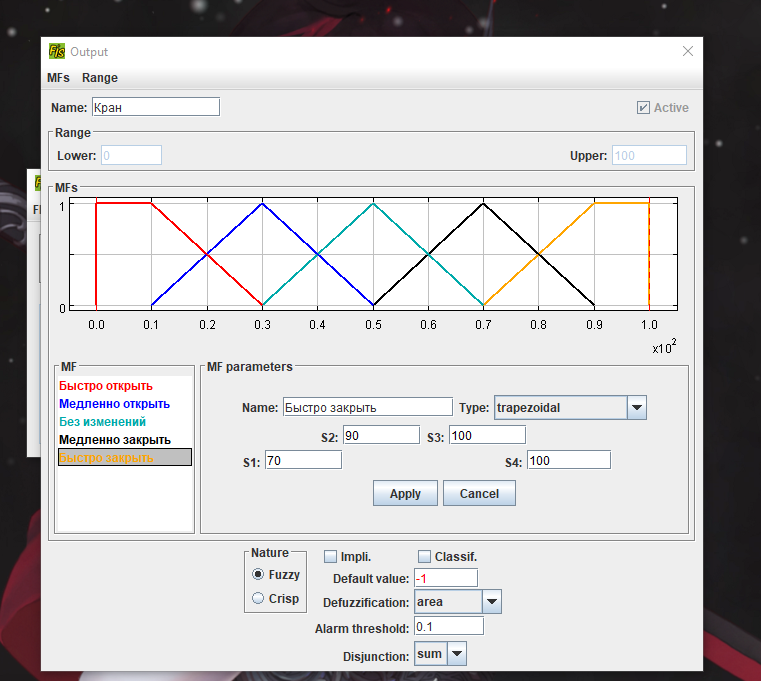 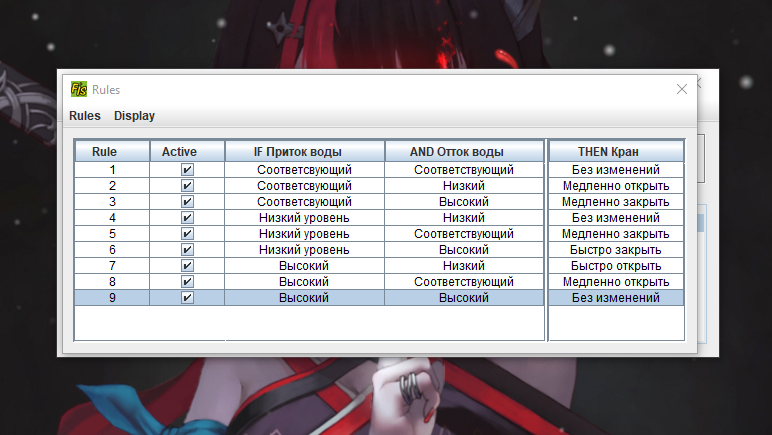 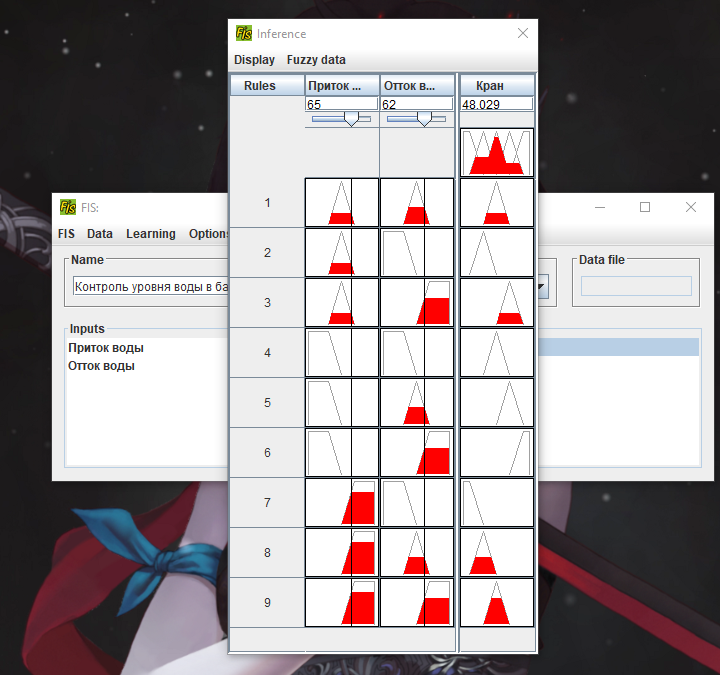 Вывод:С помощью ФисПро мы научились работать с нечеткими множествами. 6. Контрольные вопросыКакие переменные называются лингвистическими? Лингвистическими называются переменные, значениями которых являются термы (слова, предложения). С термином “лингвистическая переменная” можно связать любую физическую переменную, для которой нужно иметь больше значений, нежели, да и нет. Значения лингвистической переменной принято называть термами. Какие этапы включает в себя процесс проектирования нечетких систем? В целом процесс вычисления в нечетких системах происходит в несколько этапов: 1) Фаззификация 2) Нечеткий логический вывод 3) Дефаззификация В чем заключается процесс фаззификации? Фаззификация - процесс перехода от “четкого” (измеренного, например 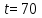 ) значения к “нечеткому” ( ) значения к “нечеткому” (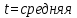 ). ). В чем заключается процесс дефаззификации? На последнем этапе, который принято называть дефаззификацией, осуществляется переход от нечетких значений к четким. Дефаззификация возможна одним из следующих методов: метод центра тяжести, модифицированный метод тяжести, метод максимума, метод левого максимума, метод правого максимума. Какие методы дефаззификации были использованы вами при построении нечетких систем? В чем эти методы заключаются? Дефаззификация выполняется по алгоритму Сугено. Метод максимума- минимума. Метод максимума-минимума учитывает только предельные отклонения звеньев размеров цепи и самые неблагоприятные их сочетания, обеспечивает заданную точность сборки без подгонки деталей, то есть полную взаимозаменяемость. Как формулируются правила нечеткого вывода для случая одной входной переменной, для случая двух входных переменных? Либо с одним условием, либо с 2мя. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


