Решение задач вычислительной математики с помощью программ Excel и Mathcad
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра «Информатика и программное обеспечение» КУРСОВАЯ РАБОТА по курсу «Информатика» Тема: «Решение задач вычислительной математики с помощью программ Excel и Mathcad» Выполнил.cт гр 17-ИСТ1: ________Мищенко А. О. Проверил: ________преп. Зимин С.Н БРЯНСК 2017 ОглавлениеВведение. 3 1.Задание №1. 4 1.1. Условие задачи 4 1.2. Решение в Mathcad 4 1.3. Решение в Excel 5 2.Задание №2. 9 2.1. Условие задачи №2 9 2.2.Расчет матрицы в Mathcad 9 2.3. Расчет матрицы в Excel 10 3.Задание №3. 11 3.1.Условие задачи №3 11 3.2.Решение нелинейных уравнение в Mathcad 11 3.3.Решение нелинейных уравнение в Mathcad 12 4.Задание№4. 13 4.1.Условие задачи №4 13 4.2.Решение задачи в Mathcad 13 4.3.Решение задачи №4 в Excel 17 5.Задание№5 20 5.1.Условие задачи №5 20 5.3.Решение в Excel 21 Заключение. 24 Введение.XXI век невозможно представить без разнообразных компьютерных технологий. За последнее десятилетие важность применения которых трудно оспорить. Ни одна сфера деятельности людей не может обходиться без компьютеров. В настоящее время для расчетов на ЭВМ используются электронные таблицы и специальные математические программы. Говоря об электронных таблицах, мы имеем в виду Excel. Математическая же программа у нас ассоциируется в основном с Mathcad. Оба эти пакета задумывались для решения финансовых, научно-технических и прочих прикладных задач. Целью курсовой работы является сравнение Mathcad и Excel при решении схожих задач, совершенствование уже имеющихся знаний и получение новых навыков в освоении этих пакетов программ. 1.Задание №1.1.1. Условие задачиДана нелинейная функция вида 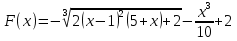 . Решить уравнение F(x)=0 и найти точки экстремума F(x) с помощью программ Excel и Mathcad. . Решить уравнение F(x)=0 и найти точки экстремума F(x) с помощью программ Excel и Mathcad.1.2. Решение в MathcadС помощью программы Mathcad построим график функции 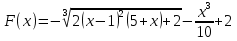 . на интервале [-5;5] (рис. 1). По графику определяем приближенные значения корней уравнения . на интервале [-5;5] (рис. 1). По графику определяем приближенные значения корней уравнения 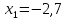 ; ; 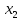 =7,5; =7,5; 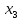 =12,5 =12,5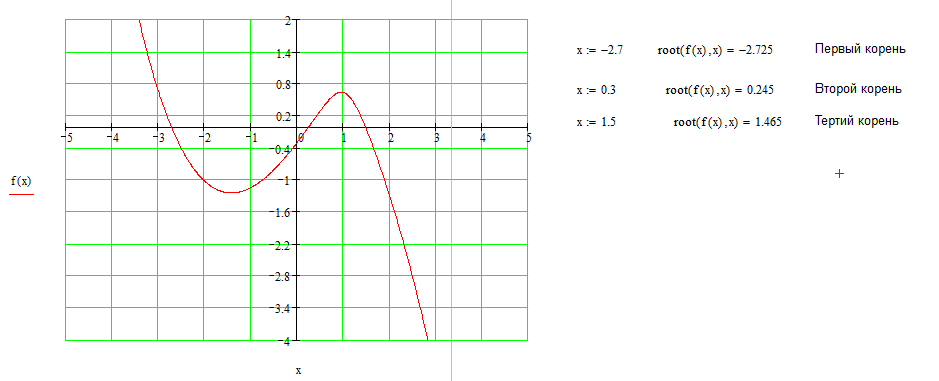 Рис.1.График функции f(x), построенный Mathcad С помощью функции «root» находим точные значения корней уравнения 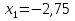 ; ;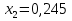 ; ;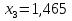 Построим график производной функции f(x). По графику определяем приближенное значение корней fs( 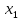 )=-1,5; fs( )=-1,5; fs(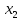 )=1. С помощью функции «root» находим точное значение корней уравнения )=1. С помощью функции «root» находим точное значение корней уравнения 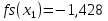 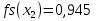 (Рис. 2). (Рис. 2).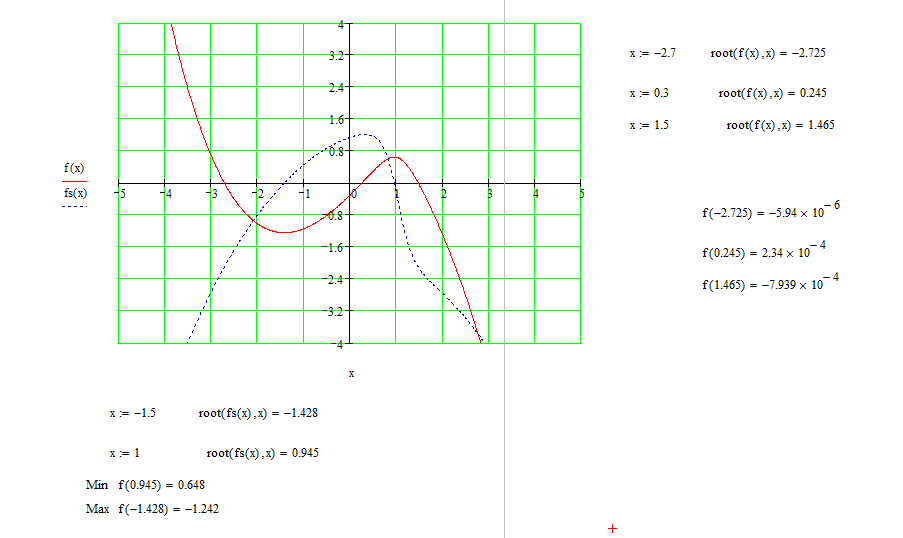 Рис.2.Нахождение корней уравнения и экстремума функции с помощью Mathcad 1.3. Решение в ExcelВыполним табулирование функции 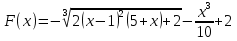 в Excel на промежутке [-5;5] с шагом 0,2 в Excel на промежутке [-5;5] с шагом 0,2На основе полученной таблицы табуляции строим график функции f(x) (рис. 3). 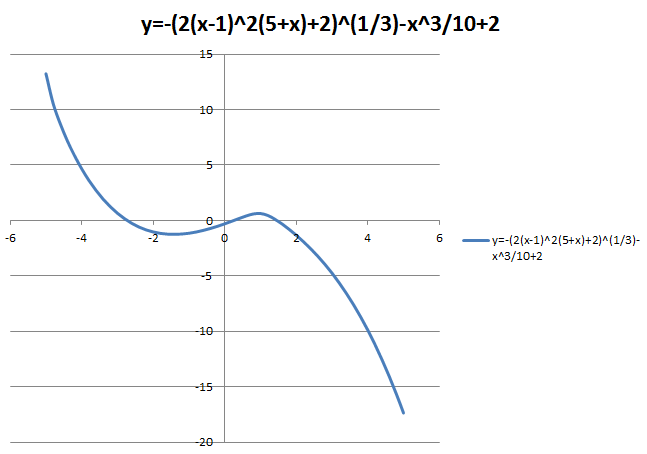 Рис. 3.Табуляция функции и построение графика в Excel На полученном графике определяем приближенные значения корней уравнения. Данные корни будут находиться в точках пересечения графика функции с осью абсцисс, а также их приближенные значения можно определить по таблице табуляции в строках, где значения в столбце y меняют свой знак. Получаем следующие приближенные значения корня уравнения: 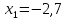 ; ; 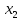 =7,5; =7,5; 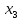 =12,5. С помощью процедуры «Подбор параметра» определяем точное значение корня для приближенного значения. Получаем следующие значение корней уравнения: =12,5. С помощью процедуры «Подбор параметра» определяем точное значение корня для приближенного значения. Получаем следующие значение корней уравнения: 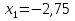 ; ; 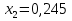 ; ; 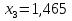 (рис.4). (рис.4).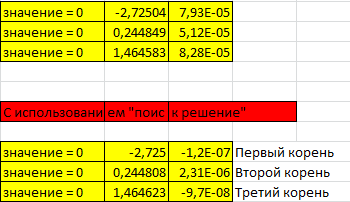 Рис. 4.Фрагмент листа Excel с найденными корнями уравнения Найдем в Excel экстремумы функции f(x). По графику видно, что данная функция имеет две точки экстремума (максимум) в районе х=1и (минимум) в районе х=-1,4. Скопируем данные из таблицы табуляции для поиска минимума. Для нахождения этих экстремумов, воспользуемся надстройкой «Поиск решения» и настроим ее согласно (рис.5). Отсюда видно, что 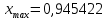 . Аналогично находим точку минимума, которая равна . Аналогично находим точку минимума, которая равна 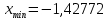 . . Рис. 5.Настройка «Поиска решения» для задачи нахождения экстремумов 2.Задание №2.2.1. Условие задачи №2Даны матрицы A,B,C. 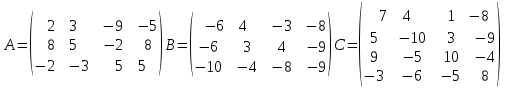 Вычислить матрицу D по формуле 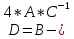 .Задание выполнить в Excel и Mathcad. .Задание выполнить в Excel и Mathcad.2.2.Расчет матрицы в MathcadРасчет матрицы D средствами Mathcad показан на рис. 6. 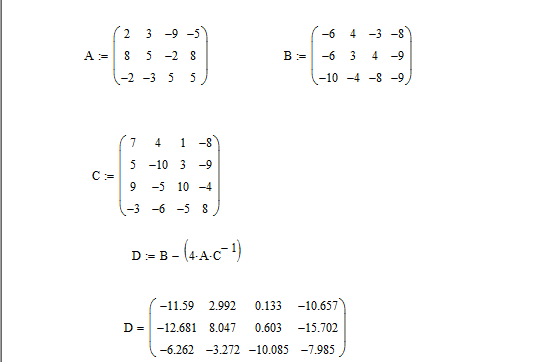 Рис.6. Вычисление матрицы D в Mathcad 2.3. Расчет матрицы в ExcelВычислим значение матрицы D c помощью Excel. (рис.7). 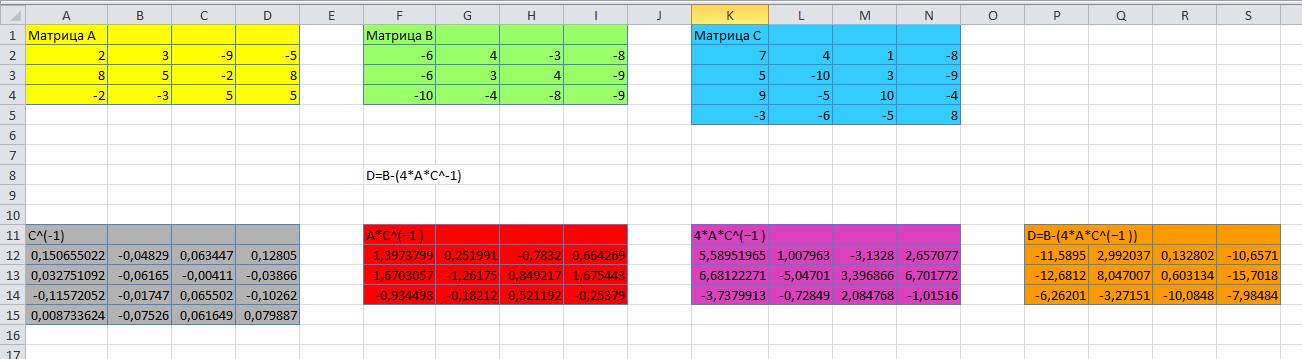 Рис.7. Вычисление матрицы D в Excel 3.Задание №3.3.1.Условие задачи №3Используя коэффициенты полученной матрицы D(задание 2) решить систему следующих нелинейных уравнений: 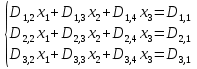 Задание выполнить в Excel и Mathcad. 3.2.Решение нелинейных уравнение в MathcadРешение системы уравнений в Mathcad приведено на рис. 8.  Рис. 8. Решение системы уравнений с помощью Mathcad 3.3.Решение нелинейных уравнение в MathcadРешим следующую систему линейных уравнений, используя коэффициенты из полученной матрицы D в Excel с применением последовательности операций линейной алгебры, а именно – с применением обратной матрицы (рис. 10).  Рис. 10. Решение системы нелинейных уравнений с помощью Excel 4.Задание№4.4.1.Условие задачи №4
Выполним это задание для следующих точек(Таблица1) Таблица1 Заданные точки
4.2.Решение задачи в MathcadПроведем кусочно-линейную интерполяцию с помощью функции «linterp» для заданных точек и определяем значение функции для указанных значений аргумента(таблица2)(рис. 11): Таблица2 Значения функции для указанных значений аргумента
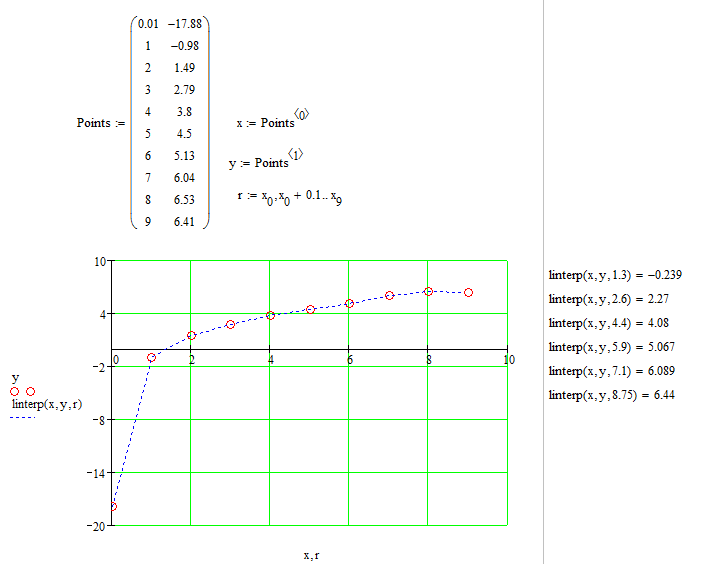 Рис.11. Кусочно-линейная интерполяция в Mathcad Проведем полиномиальную интерполяцию с помощью функции «regress». Учитывая, что задано 10 точек, то полином должен быть 9-й степени. Построим его график, на котором отметим исходные точки (рис. 12). По графику можно убедиться, что полином проходит через все заданные точки. 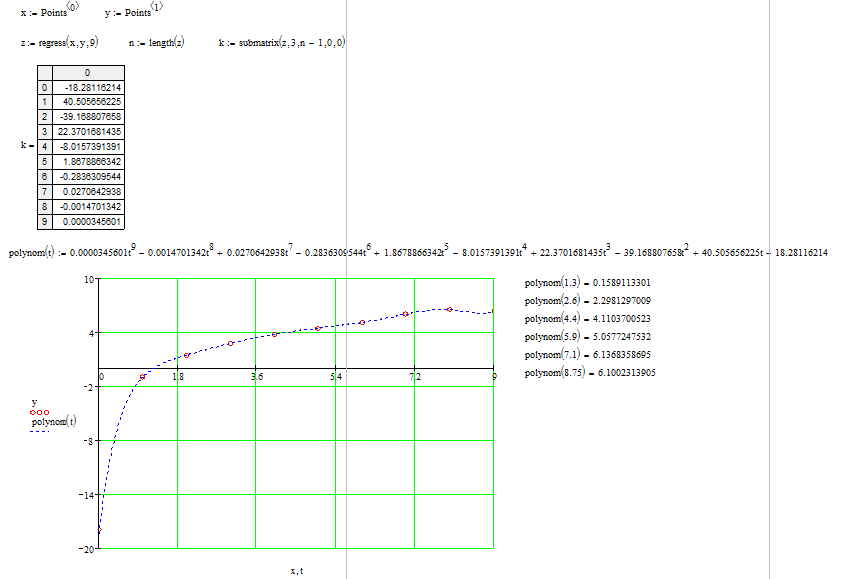 Рис.12. Полиномиальная интерполяция в Mathcad Используя функцию «polynom», определим для заданных точек значение функции (таблица3)(рис. 12): Таблица3 Значения функции
Проведем с помощью Mathcad аппроксимацию для заданных точек с помощью линейной и логарифмической функций (рис. 13). Определим сумму квадратов отклонений для узловых точек (рис. 13):
Можно сделать вывод, что с помощью логарифмической функции мы получаем более точное приближение.  Рис.13. Аппроксимация точек в Mathcad Построим на одной координатной плоскости графики аппроксимирующих функций (Рис.14). 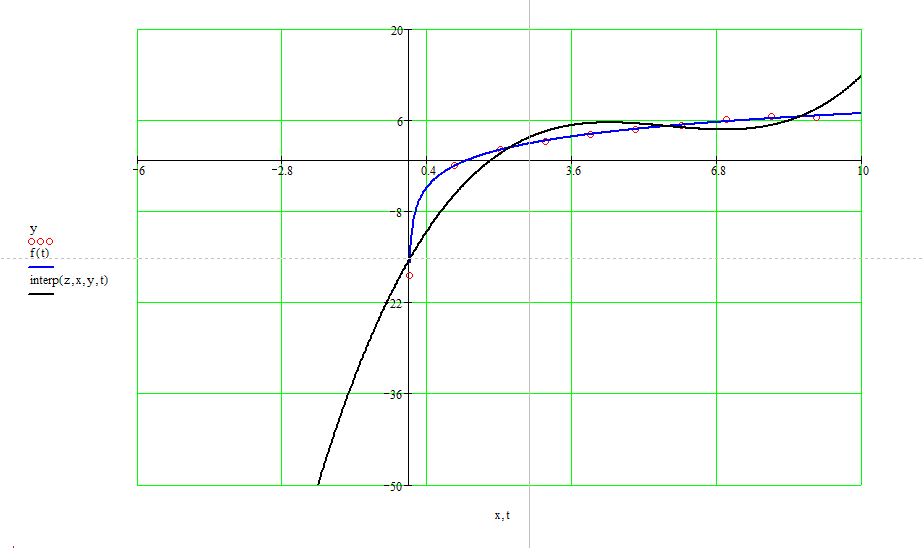 Рис.14.Графики аппроксимирующих функций Рис.14.Графики аппроксимирующих функций4.3.Решение задачи №4 в ExcelПроведем аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную таблицу точек и отметим эти точки на графике (рис. 15). 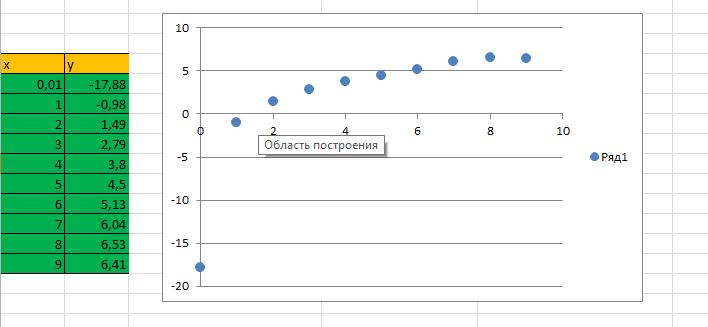 Рис. 15. Исходные точки для аппроксимации на графике Вызовем контекстное меню для одной из точек на графике и выберем пункт «Добавить линию тренда…». Для начала проведем аппроксимацию с помощью полинома 3-й степени. Для этого в открывшемся диалоговом окне «Линия тренда» выберем «Полиномиальная» и укажем степень «2». Аналогично добавим линию тренда на основе логарифмической функции. В настройках линий тренда выставим галочку «показывать уравнение на диаграмме». Результат представлен на (Рис.16). Получили следующие аппроксимирующие функции.
y = 0,1317x3 - 2,243x2 + 12,092x - 15,385
y = 3,6089ln(x) - 1,1751 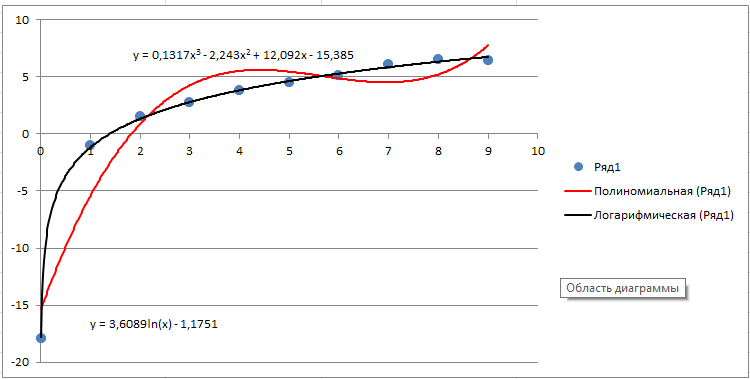 Рис.16 Получение графиков аппроксимации Определим сумму квадратов отклонений для полученных функций в узловых точках (Рис.17Error: Reference source not found). Получим:
Следовательно, аппроксимация набора данных логарифмической функции более точна, чем линейной функцией. 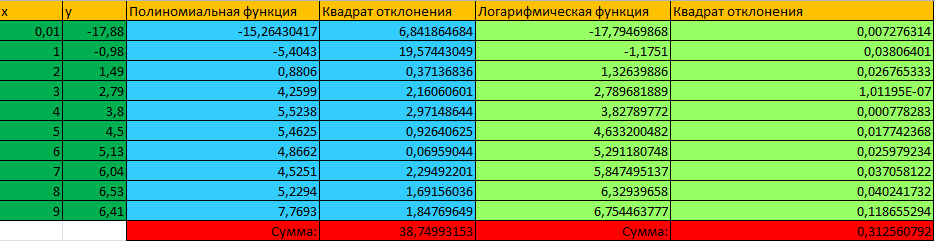 Рис. 17 Расчет суммы квадратов отклонений для аппроксимирующих функций 5.Задание№55.1.Условие задачи №5Найти экстремум функции двух переменных 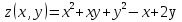 в Excel и Mathcad. Построить график двумерной поверхности в Excel и Mathcad. в Excel и Mathcad. Построить график двумерной поверхности в Excel и Mathcad. 5.2.Решение в Mathcad Построим график функции в Mathcad (Рис.18) 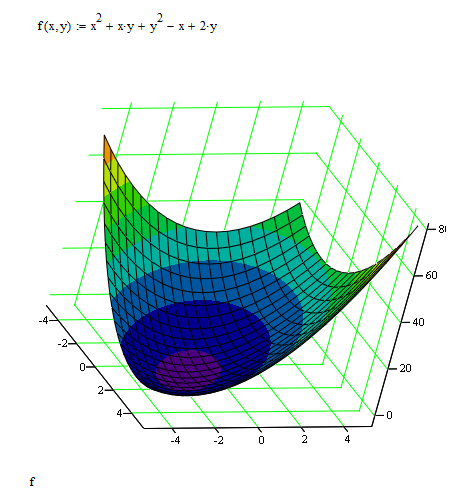 Рис.18 Построение поверхности в Mathcad По графику определяем, что функция z имеет только один экстремум – точку минимума. Воспользуемся блоком решения Mathcad и функцией Minimize. За начальное приближение точки минимума возьмем 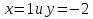 Получили решение 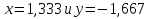 (Рис.19). (Рис.19). Рис.19 Минимизация функции в Mathcad 5.3.Решение в ExcelСначала проведем табуляцию функции с шагом 1 на интервале по x[-8;8] и y[-10;10] (Рис.20). 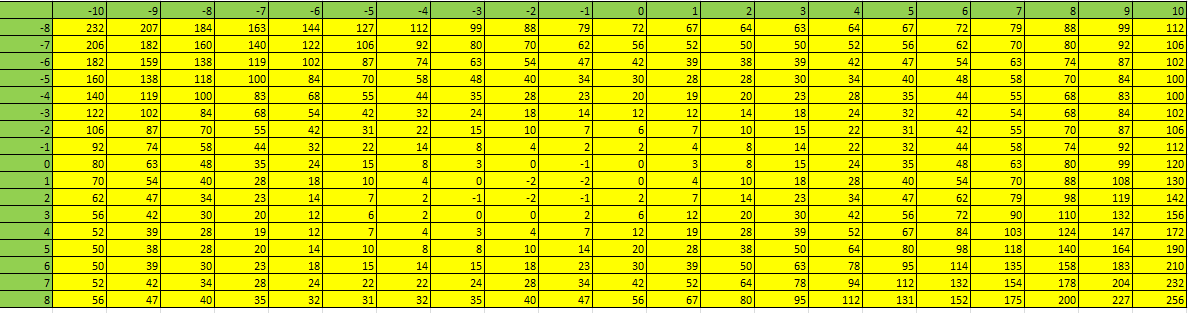 Рис.20 Табулирование функции 2-х переменных в Excel На основе полученной таблицы строим поверхность (Рис.21). 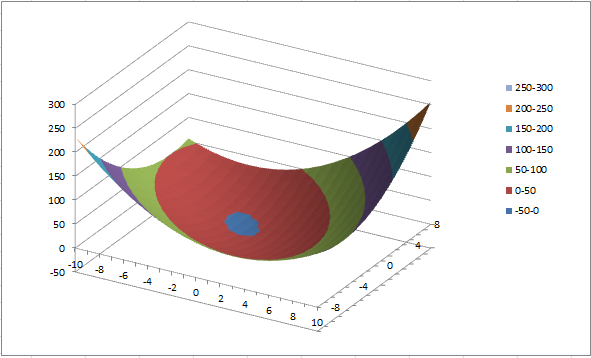 Рис.21 График функции 2-х переменных в Excel С помощью надстройки «Поиск решения» найдем точку минимума. Для этого настроим соответствующее диалоговое окно следующим образом (рис. 22). В результате выполнения получим искомую точку минимума: (Рис. 22). 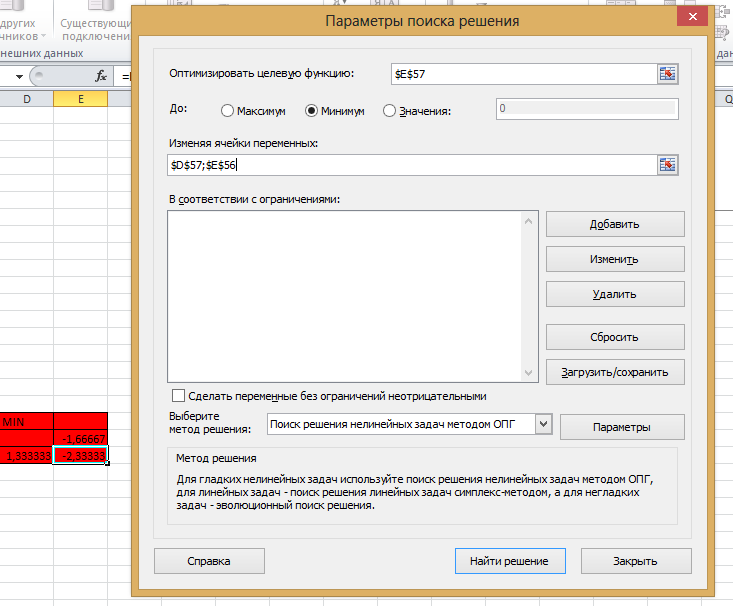 Рис. 22 Настройка «Поиска решения» для нахождения миниума Заключение.Excel и Mathcad позволяют рационально решать инженерные задачи, поставленные перед пользователем. В результате проведенной работы можно сделать вывод о преимуществе Mathcad над Excel при решении математических задач, которые были приведены в курсовой работе. Mathcad является достаточно точной и математически продуманной программой. Большое количество адресов ячеек, которые приходится записывать при вводе формул, в Excel является одним из минусов этого пакета. Ведь в случае ошибки в записи формулы найти ее будет крайне трудно. В то время как Mathcad имеет простой пользовательский интерфейс, который позволяет решать задачи, опираясь лишь на простые математические знания. Выполненная курсовая работа позволила закрепить уже имеющиеся знания об Excel и Mathcad, а также позволила узнать больше о возможностях этих пакетов программ. Кроме того, на основе практических знаний появилась возможность сказать о достоинствах и недостатках используемых, при решении задач, программ. В частности, средствами Excel нельзя выполнить линейную интерполяцию. Напротив, в математической программе MathCad, можно с легкостью выполнить линейную интерполяцию. |
