Тема 1. Задачи линейного программирования. Решение задачи линейного программирования в Excel

Название	Решение задачи линейного программирования в Excel
Анкор	Тема 1. Задачи линейного программирования.doc
Дата	22.04.2017
Размер	87 Kb.
Формат файла
Имя файла	Тема 1. Задачи линейного программирования.doc
Тип	Решение #5128

Тема 1. Применение линейного программирования в математических моделях оптимального планирования

Общая постановка задачи линейного программирования (ЗЛП).
Примеры ЗЛП.
Графический метод решения ЗЛП.
Решение задачи линейного программирования в Excel.

1. Общая постановка задачи линейного программирования (ЗЛП). Примеры ЗЛП
Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Несколько слов о самом термине линейное программирование. Он требует правильного понимания. В данном случае программирование - это, конечно, не составление программ для ЭВМ. Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:

задача об оптимальном использовании ресурсов при производственном планировании;
задача о смесях (планирование состава продукции);
задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");
транспортные задачи (анализ размещения предприятия, перемещение грузов).

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим:

математические модели большого числа экономических задач линейны относительно искомых переменных;
данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
многие задачи линейного программирования, будучи решенными, нашли широкое применение;
некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; систему ограничений в виде системы линейных уравнений или неравенств; условие неотрицательности переменных.

В общем виде модель записывается следующим образом:

1.Целевая функция:

= c₁x₁ + c₂x₂ + ... + c_nx_n → max(min);

(1)

Система ограничений:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n {≤ = ≥} b₁,
a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n {≤ = ≥} b₂,

...

a_m1x₁ + a_m2x₂ + ... + a_mnx_n {≤ = ≥} b_m;

(2)
Условие неотрицательности:

x_j ≥ 0,

(3)

При этом a_ij, b_i, c_j (

) - заданные постоянные величины.

Задача состоит в нахождении оптимального значения функции (1) при соблюдении ограничений (2) и (3).

Систему ограничений (2) называют функциональными ограничениями задачи, а ограничения (3) - прямыми.

Вектор

, удовлетворяющий ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования. План

, при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным.
2. Примеры задач линейного программирования

Далее приведем примеры некоторых типовых задач, решаемых при помощи методов линейного программирования. Такие задачи имеют реальное экономическое содержание. Сейчас лишь сформулируем их в терминах ЗЛП, а методы решения подобных задач рассмотрим ниже.
1. Задача об оптимальном использовании ресурсов при производственном планировании.

Общий смысл задач этого класса сводится к следующему.

Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b₁, b₂,..., b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида (

).

Прибыль, получаемая предприятием при реализации изделия j-го вида, равна c_j.

В планируемом периоде значения величин a_ij, b_i и c_j остаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.

Далее приведем простой пример задачи такого класса.
Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор - в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В - 72 н-часа и участка С - 10 н-часов.

Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?
Условия задач указанного класса часто представляют в табличной форме (см. таблицу 1).

Таблица 1. Исходные данные задачи об использовании производственных ресурсов

Производственные участки	Затраты времени на единицу продукции, н-час		Доступный фонд времени, н-час
Производственные участки	клюшки	наборы шахмат	Доступный фонд времени, н-час
А	4	6	120
В	2	6	72
С	-	1	10
Прибыль на единицу продукции, $	2	4

По данному условию сформулируем задачу линейного программирования.

Обозначим: x₁ - количество выпускаемых ежедневно хоккейных клюшек, x₂ - количество выпускаемых ежедневно шахматных наборов.

Формулировка ЗЛП:

= 2x₁ + 4x₂ → max;

4x₁ + 6x₂ ≤ 120,
2x₁ + 6x₂ ≤ 72,
x₂ ≤ 10;

x₁ ≥ 0, x₂ ≥ 0.

Подчеркнем, что каждое неравенство в системе функциональных ограничений соответствует в данном случае тому или иному производственному участку, а именно: первое - участку А, второе - участку В, третье - участку С.

Повторимся, методы решения ЗЛП мы будем рассматривать чуть позднее, а сейчас - пример задачи другого типа.
2. Задача о смесях (планирование состава продукции).

К группе задач о смесях относят задачи по отысканию наиболее дешевого набора из определенных исходных материалов, обеспечивающих получение смеси с заданными свойствами. Иными словами, получаемые смеси должны иметь в своем составе m различных компонентов в определенных количествах, а сами компоненты являются составными частями n исходных материалов.
На птицеферме употребляются два вида кормов - I и II. В единице массы корма I содержатся единица вещества A, единица вещества В и единица вещества С. В единице массы корма II содержатся четыре единицы вещества А, две единицы вещества В и не содержится вещество C. В дневной рацион каждой птицы надо включить не менее единицы вещества А, не менее четырех единиц вещества В и не менее единицы вещества С. Цена единицы массы корма I составляет 3 рубля, корма II - 2 рубля.

Составьте ежедневный рацион кормления птицы так, чтобы обеспечить наиболее дешевый рацион.

Представим условие задачи в таблице 2.2.

Таблица 2.2 - Исходные данные задачи о смесях

Питательные вещества	Содержание веществ в единице массы корма, ед.		Требуемое количество в смеси, ед.
Питательные вещества	корм I	корм II	Требуемое количество в смеси, ед.
А	1	4	1
В	1	2	4
С	1	-	1
Цена единицы массы корма, р	2	4

Сформулируем задачу линейного программирования.

Обозначим: x₁ - количество корма I в дневном рационе птицы, x₂ - количество корма II в дневном рационе птицы.

Формулировка ЗЛП:

= 3x₁ + 2x₂ → min;

x₁ + 4x₂ ≥ 1,
x₁ + 2x₂ ≥ 4,
x₁ ≥ 1;

x₁ ≥ 0, x₂ ≥ 0.

3. Графический метод решения ЗЛП
Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения.

Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования.

Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х₁, х₂} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁x₁ + c₂x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.
Далее рассмотрим пример решения ЗЛП графическим методом. Для этого воспользуемся представленной выше задачей о хоккейных клюшках и шахматных наборах.

1. Выше уже приводилась формулировка задачи, здесь нам остается лишь повторить ее:

= 2x₁ + 4x₂ → max;

4x₁ +6x₂ ≤ 120,
2x₁ +6x₂ ≤ 72,
x₂ ≤ 10;

x₁ ≥ 0, x₂ ≥ 0.

2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи (см. рисунок 1). Эти прямые обозначены на рисунке (1), (2) и (3).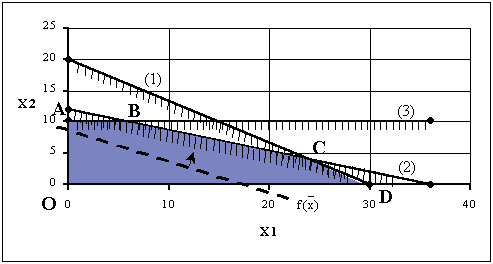

Рисунок 1. Геометрическое решение ЗЛП

3. Штрихи на прямых указывают полуплоскости, определяемые ограничениями задачи.

4. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В нашем случае область представляет собой пятиугольник (на рисунке обозначен ABCDO и окрашен синим цветом).

5. Прямая, соответствующая целевой функции, на рисунке представлена пунктирной линией.

6. Прямую передвигаем параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка C. Это и есть точка, соответствующая оптимальному решению задачи.

7. Осталось вычислить координаты точки С. Она является точкой пересечения прямых (1) и (2). Решив совместно уравнения этих прямых, найдем:

. Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке

.

Таким образом, для максимизации прибыли компании следует ежедневно выпускать 24 клюшки и 4 шахматных набора. Реализация такого плана обеспечит ежедневную прибыль в размере $64.

Решение задачи линейного программирования в Excel (см. Презентацию)