Волны. Практическое задание Волны. Решение задачи Скорость распространения колебаний можно определить через длину волны и частоту колебаний следующим образом
 Скачать 2.17 Mb. Скачать 2.17 Mb.
|
|
Практическое задание «Волны» Волна распространяется в упругой среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту колебаний. (50 Гц) Решение задачи: Скорость распространения колебаний υ можно определить через длину волны λ и частоту колебаний ν следующим образом: υ=λν Откуда частота колебаний ν равна: 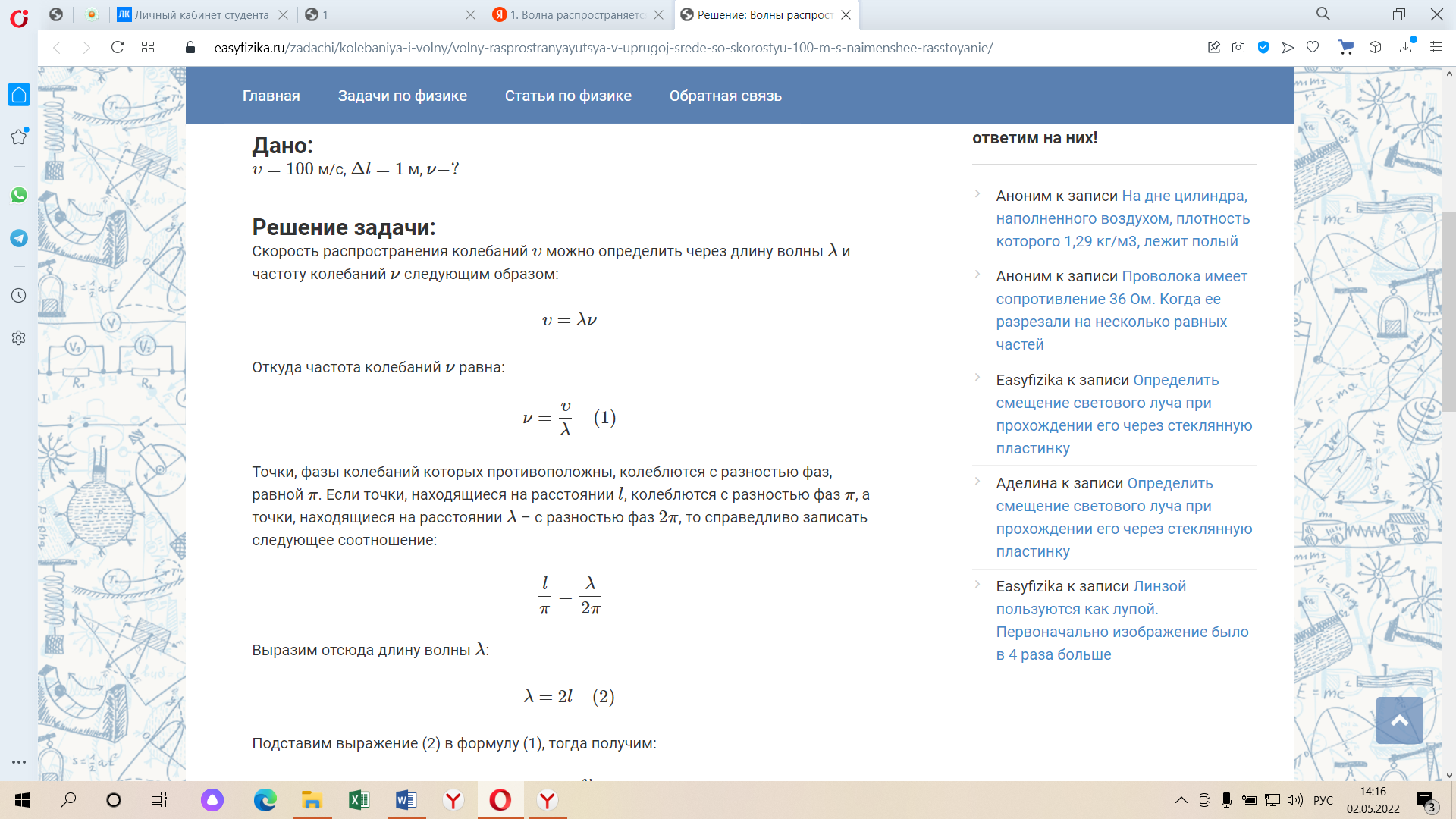 Точки, фазы колебаний которых противоположны, колеблются с разностью фаз, равной π. Если точки, находящиеся на расстоянии l, колеблются с разностью фаз π, а точки, находящиеся на расстоянии λ – c разностью фаз 2π, то справедливо записать следующее соотношение: 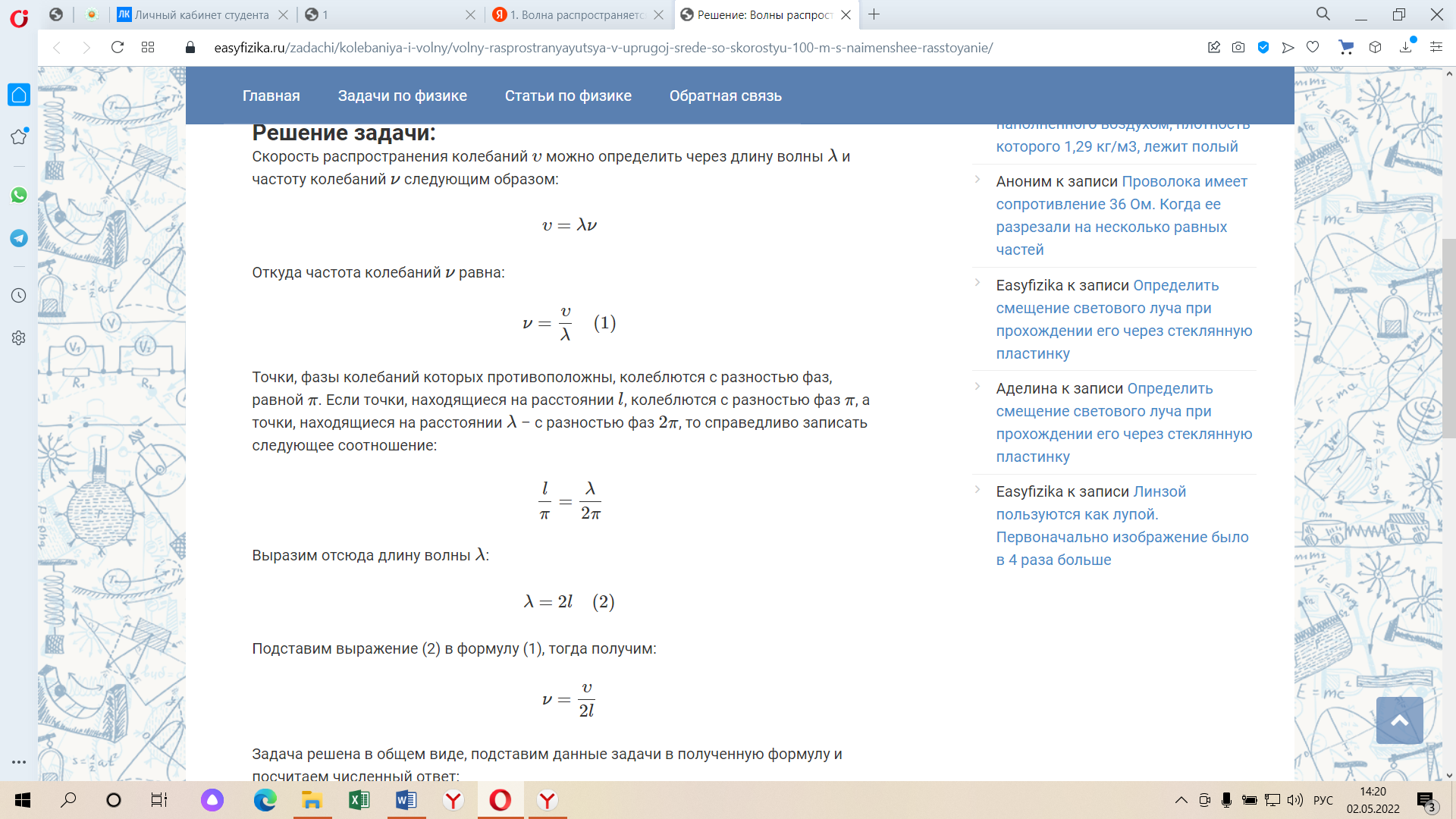 Выразим отсюда длину волны λ: λ=2l (2) Подставим выражение (2) в формулу (1), тогда получим: 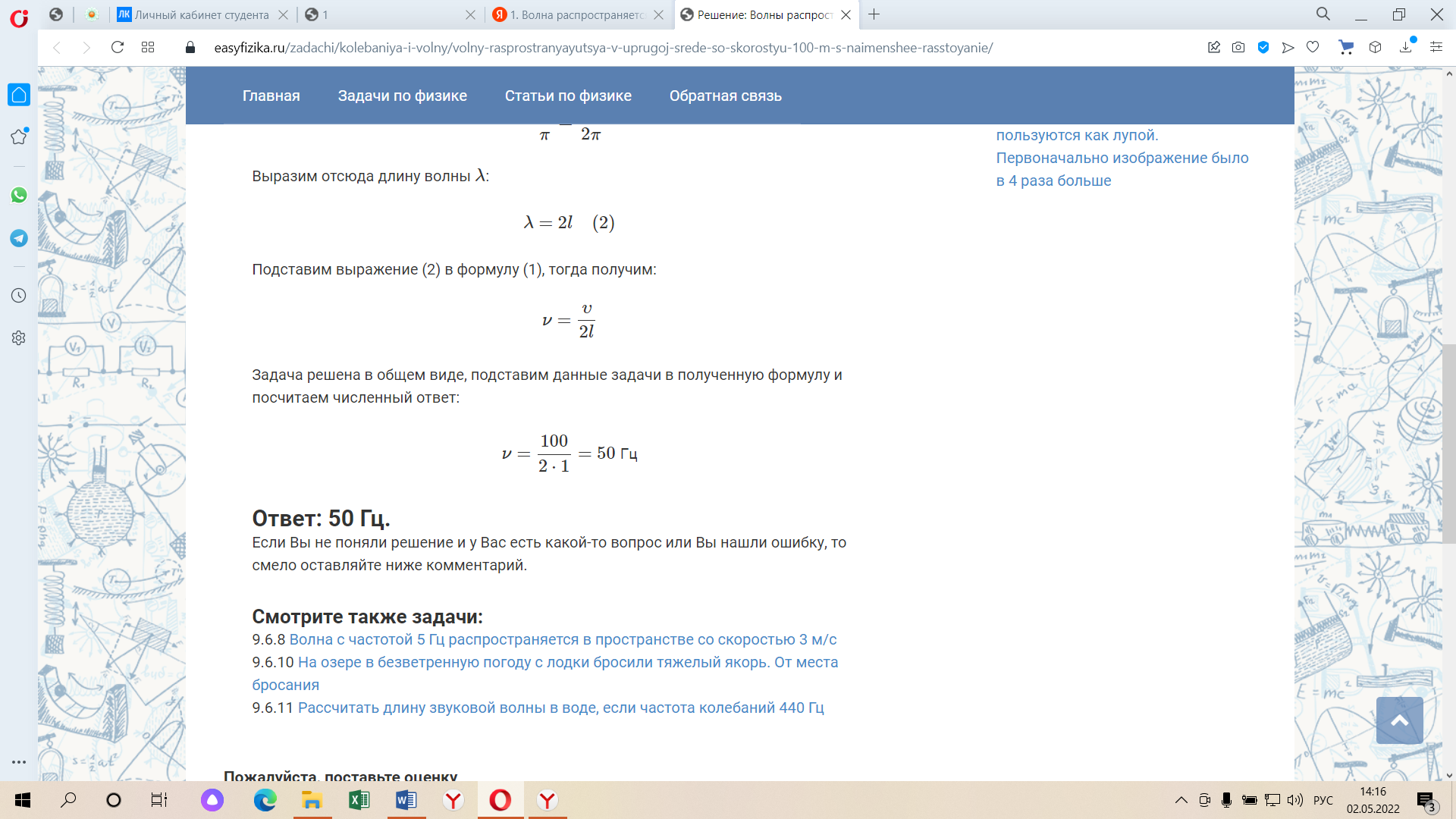  Определить скорость распространения волны в упругой среде, если разность фаз колебаний двух точек среды, отстоящих друг от друга на расстоянии 10 см, равна 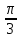 . Частота колебания равна 25 Гц. . Частота колебания равна 25 Гц.Решение: Решение. Разность фаз колебаний двух точек определяется по формуле: 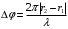 (1) (1)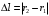 (2) (2)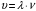 (3) (3)Подставим (2) в (1) и выразим из (1) λ и подставим λ в (3): 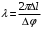 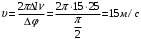 |
