Курсовой формула Чебышева. ПЗ-2 формула Чебышева 9 узлов. Решение задачи в математической системе Mathcad
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
      СОДЕРЖАНИЕ
Введение С развитием информационных технологий (ИТ) компьютеры, с их расширенными функциональными возможностями, активно применяются в различных сферах человеческой деятельности, связанных с обработкой информации, представлением данных. Особенностью настоящего времени является широкое применение математических методов и ЭВМ в различных областях человеческой деятельности: в науке, технике, экономике, медицине и даже в лингвистике. Математика - одна из самых древних наук. Труды многих ученых вошли в мировой фонд и стали основой современных алгебры и геометрии. В конце XVII в., когда развитие науки шло быстрыми темпами, появились понятия дифференцирование, а вслед за ним и интегрирование. Многие правила нахождения интеграла в то время не были известны, поэтому ученые пытались найти другие, обходные пути поиска значений. Первым методом явился метод Ньютона – поиск интеграла через график функции, т.е. нахождение площади под графиком, методом прямоугольников, впоследствии усовершенствованный в метод трапеций. Позже был придуман параболический метод или метод Симпсона и метод Чебышева. Целью курсовой работы является разработка программы расчета определенного интеграла по формуле Чебышева для случая девяти узлов. Основанием для разработки является задание на курсовую работу. Задачами курсовой работы являются: – систематизация знаний, полученных при изучении дисциплины; – приобретение опыта в комплексной разработке и реализации практических задач; – совершенствование практических навыков в использовании и разработке современных информационных систем; – практическое использование среды программирования C++Builder. 1 Описание поставленной задачи 1.1 Краткая характеристика численного метода К вычислению определенного интеграла сводятся многие практические задачи, такие, как вычисление площадей фигур, объемов тел, работы некоторой силы и др. В настоящее время существует ряд методов для нахождения интеграла. Пусть для непрерывной функции f(x), определенной на отрезке [a,b], требуется вычислить определенный интеграл Геометрически это означает, что необходимо вычислить площадь фигуры, заключенной между осью x и кривой y = f(x) и ограниченной слева и справа прямыми, проходящими через точки x = a и x = b, иначе называемой криволинейной трапецией (рисунок 1.1.1). 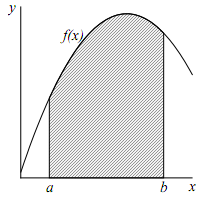 Рисунок 1.1.1 - Криволинейная трапеция Обычно понятие определенного интеграла вводится как предел интегральной суммы при неограниченном увеличении числа точек разбиения отрезка [a,b]. Интегральной суммой называется сумма площадей элементарных прямоугольников, которые получаются в результате разбиения отрезка [a,b] на n элементарных отрезков и построения боковых сторон прямоугольников, проходящих через узловые точки xi , i=0,1,2,…,n.  (1.2) (1.2) В результате этой процедуры искомая площадь криволинейной трапеции заменяется площадью ступенчатой фигуры, состоящей из суммы площадей отдельных прямоугольников, интегральной суммой. Площадь этой ступенчатой фигуры при ∆x → 0 стремится к площади криволинейной трапеции. В таких случаях могут применяться методы численного интегрирования. Вычислительный алгоритм строится следующим образом. Отрезок интегрирования [a,b] разбивается на n равных частичных отрезков [xi-1, xi], i=1,2, ...,n длиной h=(b-a)/h, а интеграл заменяется суммой частичных интегралов  (1.4) (1.4)Затем подынтегральная функция f(x) на частичном отрезке [xi-1, xi] заменяется некоторым интерполяционным полиномом невысокой степени m Lm, i (x) и вычисляется интеграл В результате получается приближенное значение интеграла  (1.6) (1.6)Эта формула называется квадратурной, точки xk – узлами, а числа ck – коэффициентами этой формулы. Погрешность квадратурной формулы определяется из выражения  (1.7) (1.7)В зависимости от выбора интерполяционного Lm,i(x) получаются различные квадратурные формулы. Это могут быть формулы прямоугольников, трапеций, Гаусса, Чебышева и другие. Пусть требуется найти определенный интеграл по квадратурной формуле Чебышева. Рассмотрим, что представляет собой квадратурная формула, и как можно с ее помощью вычислить приближенно интеграл. Известно, численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y=  Рисунок 1.1.2 - Криволинейная трапеция Если f(x) непрерывна на отрезке [a, b], и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по, известной всем, формуле Ньютона - Лейбница где F’(x) = f(x) Однако во многих случаях F(x) не может быть найдена, или первообразная получается очень сложной для вычисления. Кроме того, функция часто задается таблично. Поэтому большое значение приобретает приближенное и в первую очередь численное интегрирование. Задача численного интегрирования состоит в нахождении приближенного значения интеграла Численное определение однократного интеграла называется механической квадратурой, а соответствующие формулы численного интегрирования - квадратурными. Заменяя подинтегральную функцию каким-либо интерполяционным многочленом, получим квадратурные формулы вида где xk - выбранные узлы интерполяции; Ak - коэффициенты, зависящие только от выбора узлов, но не от вида функции (k=0,1,2,........, n). R - остаточный член, или погрешность квадратурной формулы. Отбрасывая остаточный член R, мы совершаем погрешность усечения. При расчете к ней добавляются еще различные погрешности округления. Разобьем отрезок интегрирования [a, b] на n равных частей системой точек xi= x0+ i..h; ( i = 0,1,2,......,n) x0= a; xn= b; h= (b-a)/n ; и вычислим подинтегральную функцию в полученных узлах yi= f(xi) ; ( i = 0,1,2,......,n) Теперь рассмотрим несколько простейших квадратурных формул: Рассмотрим квадратурную формулу вида: функцию f(x) будем искать в виде когда f(x) многочлен вида f(x)=a0+a1x+...+anxn. Проинтегрировав, преобразовав и подставив значения многочлена в узлах f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n . . . . . . . . . . . . . . . . f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn получим формулу Чебышева. где n – число узлов. Значения х1,х2,..,хn для различных n приведены в таблице 1.2.1. Таблица 1.2.1 – Значения х1,х2,..,хn для различных n
1.2 Анализ литературы и программ, патентный поиск Анализ литературы показал, что в зависимости от вида выражения квадратуры для нахождения значения определенного интеграла используются следующие численные методы: правых, левых и средних прямоугольников; трапеций; формулы Симпсона и Буля; Монте-Карло; формулы Гаусса-Лежандра, рекуррентные формулы. В зависимости от степени производной, учитываемой численным методом, определяется степень точности метода. Шаг интегрирования может быть постоянным на всём расчётном интервале аргумента X или изменяться в зависимости от величины ошибки определения функции. Для того чтобы внедрить инновационный продукт без опасения нарушения чьих-то интеллектуальных прав, необходимо предварительно провести патентно-информационный поиск. Возможно, аналогичное изобретение уже было зарегистрировано, что сделает невозможным коммерческое использование инновации без нарушения прав третьих лиц. Патентный поиск осуществляется посредством информационно-поисковой системы Google.com и выполняется вручную. Основные цели патентного поиска: – поиск дополнительных информационных материалов; – определение состояния исследований в интересуемом информационном поле. Результаты патентного поиска: – www.exponenta.ru; – http://matlab.exponenta.ru/spline/book1/16.php; – http://www.intuit.ru/department/calculate/intromathmodel/4/. 1.3 Формирование требований к программе Разрабатываемая программа должна удовлетворять следующим требованиям: 1) тип операционной системы – Windows XP и выше; 2) система программирования – Borland C++ Builder 3) формат файла исходных данных – текстовый; 4) форма вывода результатов расчета: результат решения с сохранением в текстовый файл; 5) форма задания решаемого нелинейного уравнения – в виде подпрограммы; 6) математические системы тестирования – Mathсad. 2 Проектирование схем алгоритмов 2.1 Разработка алгоритма головной программы Схема алгоритма головной программы описывает общий сценарий работы разрабатываемого приложения. В составе проекта приложения предусматривается три формы: 1) главная форма приложения; 2) форма ввода исходных данных; 3) форма информации о программе. Результаты расчета размещаются на главной форме. При запуске приложения отображается главная форма, на которой находятся управляющие элементы: главное меню и кнопки. В схеме головного алгоритма предусматривается обработка следующих событий (нажатие соответствующей кнопки или выбор пункта главного меню): 1) вызов формы для ввода исходных данных; 2) нахождение интеграла, при условии ввода исходных данных; 3) отображение результатов расчета, при условии успешного расчета; 4) вывод формы с информацией о программе; 5) выход из программы. В схеме алгоритма предусматривается контроль и блокирование следующих действий пользователя: 1) запуск решения при отсутствии ввода исходных данных; 2) просмотр результатов расчета без успешного завершения этапа численного решения. Схема алгоритма головной программы изображается согласно требованиям ГОСТ 19.701-90 на рисунке 2.1  Рисунок 2.1 – Схема алгоритма головной программы 2.2 Проектирование алгоритма ввода исходных данных Функция Y=f(x) задается в виде подпрограммы f с одним параметром. Параметр x – текущее значение аргумента. В программе исходными данными являются: – значения интервала расчетов - начало отрезка а и конец отрезка b; – количество узлов N. – счетчик итераций i; – значение шага интервала h; – значения аргумента функции x[i] в зависимости от числа узлов; Выходные результаты решения: – значение интеграла J; Ввод исходных данных выполняется с формы. Схема алгоритма ввода исходных данных представлена ниже на рисунке 2.2. 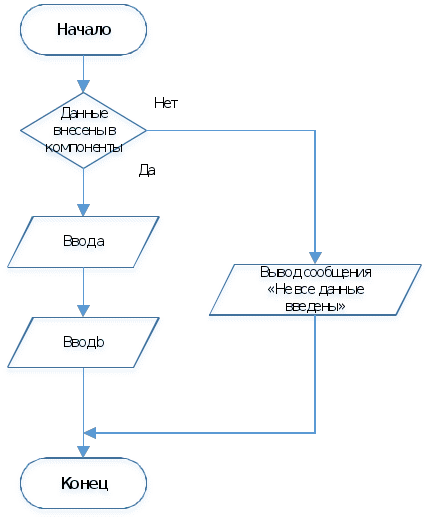 Рисунок 2.2 – Схема алгоритма ввода исходных данных 2.3 Разработка алгоритма вывода результатов Результаты расчета выводятся в компонент-список на каждом шаге вычисления. Следовательно, блок вывода включен в схему алгоритма численного метода. В курсовой работе рассматривается сохранение результатов в текстовый файл, так как компонент-список имеет метод – сохранение в файл. Открытие и закрытие файла производится автоматически при использовании метода сохранения в файл, поэтому на схеме алгоритма не отображаются. Схема алгоритма записи в файл представлена на рисунке 2.3. 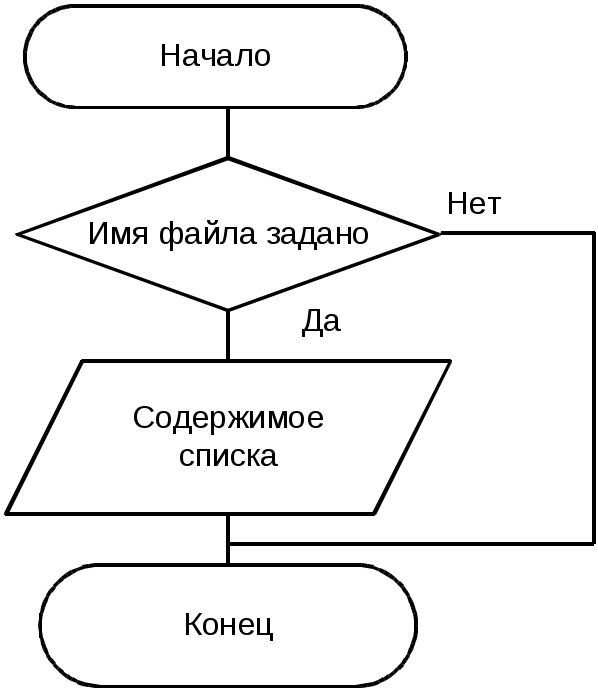 Рисунок 2.3 – Схема алгоритма вывода значений в файл 2.4 Проектирование алгоритма численного метода Определение интеграла методом Чебышева оформляется в виде отдельной подпрограммы. Вычисления производятся N раз (количество узлов N=9 по условию задачи). На каждом этапе производится вычисление у и производится вывод полученных данных на форму. Cheb() - функция для вычисления интеграла методом Чебышева. Блок-схема алгоритма представлена на рисунке 2.4. 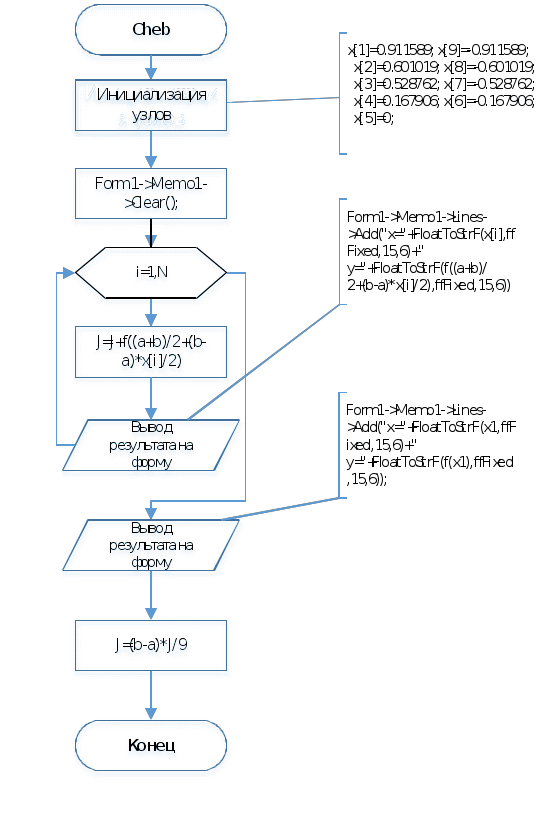 Рисунок 2.4 – Схема алгоритма нахождения интеграла методом Чебышева 3 Кодирование программы в среде программирования 3.1 Разработка структуры программы Согласно заданию проект программы разрабатывается в среде визуального программирования С++Builder версии 6.0 на основе составленных в предыдущем разделе схем алгоритмов. Для удобства и гибкости работы с различными видами нелинейных уравнений запись производной выполняется в виде подпрограммы-функции f(x). Создаваемое в среде C++ Builder приложение состоит из нескольких элементов, объединенных в проект. В состав проекта входят следующие элементы: код проекта; описание форм; модули форм; модули; параметры проекта; описание ресурсов. Файл проекта является центральным файлом проекта и представляет собой собственную программу. Имя проекта (программы) совпадает с именем файла проекта и указывается при сохранении этого файла на диске, первоначально это имя Project1. То же имя имеют файлы ресурсов и параметров проекта, при переименовании файла проект данные файлы автоматически переименовывается. Программа проекта содержит всего три оператора, выполняющих инициализацию приложения, создание формы Form1 и запуск приложения. Для каждой формы в составе проекта автоматически создаются файл описания (DFM) и файл модуля (cpp). Файл описание формы является ресурсом C++ Builder и содержит характеристики формы и ее компонентов. Разработчик обычно управляет этим файлом через окно Конструктора формы и Инспектор объектов. При конструировании формы в файл описания автоматически вносятся соответствующие изменения. Файл модуля формы содержит описание класса формы, создается Delphi автоматически при добавлении новой формы. По умолчанию к проекту добавляется новая форма типа TForm, не содержащая компонентов. Весь курсовой проект выполнен в C++ Builder. Вся программа хранится на дискете в папке Курсовая работа. В этой папке хранятся все Unit и Project, а также другие файлы, необходимые для корректной работы программы. - файл проекта (*.dpr) – project1.bpr – этот текстовый файл используется для хранения информации о формах и модулях. В нем содержатся операторы инициализации и запуска программы на выполнение: - файлы модулей (u*.cpp) – текстовые файлы модулей, используемые для хранения кода; - файлы форм (*.dfm) – двоичные или текстовые файлы, создаваемые для хранения форм; - файл параметров проекта (project1.Dof) – в этом файле хранятся установки параметров проекта; - файл информации о пакетах (*.drf) - бинарный файл, создаваемый при работе с пакетами; - файл ресурсов (*.res) – бинарный файл, содержащий, используемую пакетом пиктограмму и прочие ресурсы; - файл пакета (*.dpk) – двоичный файл пакета; - файлы резервных копий (*.dp, *.df, *.cp) - файлы резервных копий для файлов проекта, формы и модуля; - файл конфигурации окон (*.dsk) – файл хранит конфигурацию всех окон. Следующие файлы создаются компилятором: исполняемый файл (*.exe), объектные файлы модуля (.dcu), динамически присоединяемая библиотека (.dll), файл содержания пакета (.dcp), откомпилированный файл пакета времени выполнения (.bpl), файлы изображения (.wmf, .bmp, .ico). В пакет выполняемых файлов входят файлы с расширением .dcu, .ddp, .dfm, .dof, .dpr, .exe, .cpp; Файлы модулей содержат процедуры для работы с данными. Каждая процедура соответствует обработчику какого-либо события, например, нажатия на кнопку, активации формы, выбора пункта меню. Программный код данной программы написан на языке C++, весь программный код продемонстрирован в Приложении Б. В состав приложения входят следующие подпрограммы: 1) нажатие на кнопку «Вычислить» и отображение результатов на форме; 2) сохранение результатов в файл; 3) вычисление интеграла методом Чебышева. Проект включает в себя две формы: 1) основная форма; 2) форма со справочными данными. 3.2 Разработка интерфейса пользователя Одним из основных компонентов приложения является форма, из которой пользователь управляет событиями, происходящими во время работы приложения. Главная форма программы, раскрывается при запуске программы и содержит следующие элементы: - заголовок приложения с изображением собственной пиктограммы; - главное меню в верхней части формы; - кнопки для вызова процедур расчетов, очистки полей ввода и выхода из программы; - поля ввода исходных данных. Форма приложения представлена на рисунках 3.2.1.  Рисунок 3.2.1 – Форма приложения до выполнения 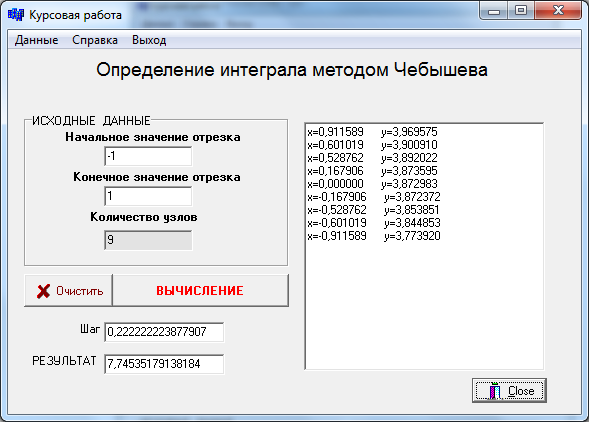 Рисунок 3.2.2 – Форма приложения после выполнения  Рисунок 3.2.3 – Форма для вывода информации о программе На форме размещены следующие компоненты: – Edit – однострочное редактируемое поле ввода. Предназначено для отображения или редактирования одной текстовой строки. Расположено для вывода полученного после вычисления результата на форму. Было изменено свойство text. – Label – метка. Этот компонент используется для размещения в окне не очень длинных однострочных надписей. Компонент расположили для подписи полей Edit. При использовании было изменено свойство Caption. – Button и SpeedButton – кнопки. Обработчик события OnClick этих компонентов обычно используется для реализации некоторой команды. При нажатии на SpeedButton1_VichislitClick вычисляется значение интеграла. 3.3 Программирование ввода-вывода данных Ввод исходных данных в проекте реализован с использованием компонентов Edit и его свойства Text. Для перевода к числовому типу используется функция StrToFloat. Так, например, ввод левой границы отрезка имеет вид: а=StrToFloat(Edit1->Text) Если данные введены не все то пользователю выводится сообщение и расчет не производится. Вид сообщения представлен на рисунке 3.4.  Рисунок 3.3.1 – Сообщение пользователю Для вывода всех полученных точек используется компонент Memo1 и его свойство Lines. Так, например, вывод текущего значения имеет вид: Form1->Memo1->Lines->Add("x="+FloatToStrF(x[i],ffFixed,15,6)+" y="+FloatToStrF(f((a+b)/2+(b-a)*x[i]/2),ffFixed,15,6)); Сохранение всех данных в файл имеет вид: if (SaveDialog1->Execute()) { Memo1->Lines ->SaveToFile(SaveDialog1->FileName); } 3.4 Программная реализация численного метода Исходное уравнение, представленное выражением float f(float x) { float y=pow((pow(x,3)+15),1./2.); return y; } Программная реализация метода выполняется на основе разработанной схемы алгоритма рисунка 2.4 в функции SpeedButton1_VichislitClick. Для возможной записи в составе уравнения математических функций в начале программы подключается стандартный модуль math.h. Тексты cpp файла модуля помещается в Приложение А. Для выполнения основных расчетов по методу Чебышева использован следующий программный код: J=0; //инициализация значения интеграла x[1]=0.911589; x[9]=-0.911589; //инициализация узлов x[2]=0.601019; x[8]=-0.601019; x[3]=0.528762; x[7]=-0.528762; x[4]=0.167906; x[6]=-0.167906; x[5]=0; for (i=1;i<=N;i++) { J=J+f((a+b)/2+(b-a)*x[i]/2); //определение значения интеграла по формуле Чебышева Form1->Memo1->Lines->Add("x="+FloatToStrF(x[i],ffFixed,15,6)+" y="+FloatToStrF(f((a+b)/2+(b-a)*x[i]/2),ffFixed,15,6)); //вывод значения расчета интеграла на форму }; J=(b-a)*J/9;// уточнение полученной суммы Form1->Edit5->Text=FloatToStr(J); //вывод значения расчета интеграла на экран в поле редактирования 4 Тестирование работоспособности программы 4.1 Описание аппаратной конфигурации для тестирования 1) тип центрального процессора Intel Celeron G1820: – основан на микроархитектуре Intel Haswell; – число ядер – 1, потоков 2; – базовая частота 200 МГц, номинальные частоты достигаются применением множителей; – частота графического ядра 1050 МГц; 2) системная плата Biostar H61MGV3 с параметрами: – форм-фактор Micro ATX; – чипсет Intel H61 Express; – процессорный разъем Intel LGA1155 – тип интерфейса подключения видеоадаптера - PCI Express 3.0; – максимальный объем оперативной памяти - 16 Гб; – интерфейс подключения жесткого диска - SATA; – встроенный аудиоадаптер VIA VT1705CF. 6-канальное; 3) установлено 1 модуль оперативной памяти GoodRam 2Gb PC1333; 4) типы внешней памяти компьютера: – тип жесткого диска - Seagate; – максимальный объем в 1500 ГБ; – частота вращения шпинделя - 7200 об/мин; – интерфейс подключения: SATA-2; – объем кэш- памяти жесткого диска - 32 МБ; – значения скорости 40/40/16; 6) параметры монитора: – тип ЖК-монитора – Samsug SyncMaster 223 bw; – ширина диагонали экрана - 19 дюймов; – интерфейс подключения к компьютеру - VGA; – разрешение по горизонтали и вертикали - 1920 x 1080; – кадровой развертки - 50 Гц; 7) состав интерфейса для подключения периферийных устройств: – 4 разъема стандарта USB2.0; – 1 разъем порта PS/2, 2 аудиоразъема. 4.2 Тестирование разработанной программы Под надежностью программного обеспечения понимается вероятность его работы без отказов в течение определенного периода времени, рассчитанная с учетом стоимости для пользователя каждого отказа. Для обеспечения надежности используют тестирование. Тестирование (testing) - процесс выполнения программы или части программы, с намерением или целью найти ошибки. Программный продукт тестируется с помощью контрольного примера. Загрузочный файл разработанной программы Project.exe занимает объем 3,9 КБайт. Для тестирования программы используется уравнение вида Согласно принятой форме записи уравнение в программе описывается следующими исходными данными: 1) начало интервала а=-1; 2) конец интервала b =1; 3) число отрезков n=9 Время расчета составило менее 1 с. Результаты расчета приводятся в Приложении Б. 4.3 Решение задачи в математической системе Mathcad В Mathcad решить задачу определения интеграла для такой системы можно с помощью функции: 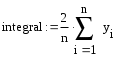 n — число узлов на отрезке [a,b]; при решении задачи на отрезке результат содержит n+1 строку; y — имя вектор-функции; Для тестирования использовался математический пакет MathCAD 2001 Professional. Результаты решения приводятся в приложении В. 4.4 Анализ результатов тестирования По данным Приложения Б (C++ Builder) получено конечное значение: J=7,74535179138184 По данным Приложения B (MathCAD) получено конечное значение: J=7,774 Абсолютное значение ошибки программы по Mathcad в=|YБ-Yв| ( 4.2 ) в = | 7,74535179138184-7,774|=0,028648209 Относительное значение ошибки теста Mathcad δв(%)=100%- |YБ-Yв|/YБ ( 4.3 ) δв (%)=100%-| 7,74535179138184-7,774|/7,74535179138184=0.0036% Так как результат представляет собой массив из N значений, для анализа выберем 5 точек. По данным Приложений Б, В получены значения: Таблица 4.1 – Результаты вычислений
Абсолютное значение ошибки программы по Mathcad в=|YБ-Yв| ( 4.2 ) Относительное значение ошибки теста Mathcad δв(%)=100%* |YБ-Yв|/YБ ( 4.3 ) Данные будут занесены в таблицу 4.2.
Для получения общей оценки погрешности следует вычислить среднее арифметическое полученных погрешностей. δв(%)=0,026 % Как видно из данных Приложений Б, В получена высокая точность расчета. Это связано с точностью, с которой выводят результаты вычислительные пакеты. Это означает, что схема алгоритма и текст программы написаны верно. Заключение В результате выполнения курсовой работы было произведено описание программы для расчета определенного интеграла методом Чебышева для случая девяти узлов, разработана схема алгоритма и написано приложение для решения задачи в среде программирования C++Builder. Проведенное тестирование показало правильность вычисления по спроектированной программе. Разработанная программа может использоваться для расчета определенных интегралов на персональных компьютерах в среде Windows 7. Разработанная программа не требует для своей работы никаких дополнительных программных компонентов и может быть запущена непосредственно с диска или другого носителя информации. Тестирование разработанной программы показало, что все компоненты системы работают корректно, программный продукт полностью отвечает предъявленным к нему требованиям. В заключение можно сделать вывод, что поставленная задача выполнена. При проектировании использованы знания, полученные на занятиях по вычислительной технике и программированию, и которые в дальнейшем помогут в будущей профессии инженера-механика при проектировании сложных узлов, механизмов и деталей машин. Список использованных источников Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика, 2004.-255 с. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения): Учеб. пособие для вузов. – М.: Высш.шк., 2000. – 266 с. Вычислительная техника и программирование. Численные методы решения алгебраических и дифференциальных уравнений. Методические указания по курсовой работе для студентов специальности Т11.02. “Автоматизированный электропривод” Часть 2. - Могилев: ММИ, 1998. – 32 с. Крылов В.И. Вычислительные методы высшей математики. Т.2/ Под ред. И.П. Мысовских. - Мн.: Выш. шк., 1975. – 672 с. Пискунов Н.С. Дифференциальное и интегральное исчисление для ВТУЗов. Т.2.; Учеб. пособие для втузов, 13-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 560 с. Плис А.И. Mathcad 2001. Математический практикум для экономистов и инженеров: Учеб. пособие / А.И. Плис, Н.А Сливина. – М.: Финансы и статистика, 2010. – 656 с. Ракитин В.И. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб. пособие/ В.И. Ракитин, В.Е. Первушин. – М.: Высш. шк., 1998. – 393 с. ГОСТ19.701-90 (ИСО 5807-85). Описание символов. Правила применения символов и выполнения схем. Вычислительная техника и программирование. Методические указания и задания к курсовому проектированию для студентов специальности 1-53 01 05 “Автоматизированный электропривод”. - Могилев: БРУ, 2014. - 31 с. Приложение А (обязательное) Тексты спроектированной программы //--------------------------------------------------------------------------- #include #pragma hdrstop #include "Unit1.h" #include "Unit2.h" #include "math.h" //--------------------------------------------------------------------------- #pragma package(smart_init) #pragma resource "*.dfm" TForm1 *Form1; int i,a=0,b=0,N=0; float h=0,S=0,J=0,x1,x2,x3,x4; //---------------------------------------------- float f(float x) { float y=pow((pow(x,3)+15),1./2.); return y; } //--------------------------------------------------------------------------- __fastcall TForm1::TForm1(TComponent* Owner) : TForm(Owner) { } //--------------------------------------------------------------------------- void cheb() { float x[10]; x[0]=0; x[1]=0.911589; x[9]=-0.911589; x[2]=0.601019; x[8]=-0.601019; x[3]=0.528762; x[7]=-0.528762; x[4]=0.167906; x[6]=-0.167906; x[5]=0; Form1->Memo1->Clear(); for (i=1;i<=N;i++) { J=J+f((a+b)/2+(b-a)*x[i]/2); Form1->Memo1->Lines->Add("x="+FloatToStrF(x[i],ffFixed,15,6)+" y="+FloatToStrF(f((a+b)/2+(b-a)*x[i]/2),ffFixed,15,6)); } J=(b-a)*J/9;//уточнение полученной суммы } //------------------------------------ void __fastcall TForm1::SpeedButton1_VichislitClick(TObject *Sender) { if ( Edit1->Text!="" && Edit2->Text!="" && Edit3->Text!="" && Edit4->Text!="" && Edit5->Text!="") { a=StrToInt(Form1->Edit1->Text); b=StrToInt(Form1->Edit2->Text); N=StrToInt(Form1->Edit3->Text); h=(float)(b-a)/N; Form1->Edit4->Text=FloatToStr(h); J=0; cheb(); Form1->Edit5->Text=FloatToStr(J); } else ShowMessage("Не все данные введены" ); } //--------------------------------------------------------------------------- void __fastcall TForm1::N3Click(TObject *Sender) { Form2->ShowModal(); } //--------------------------------------------------------------------------- void __fastcall TForm1::BitBtn2Click(TObject *Sender) { Edit1->Clear(); Edit2->Clear(); } //--------------------------------------------------------------------------- void __fastcall TForm1::N5Click(TObject *Sender) { if (SaveDialog1->Execute()) { Memo1->Lines ->SaveToFile(SaveDialog1->FileName); } } //--------------------------------------------------------------------------- void __fastcall TForm1::N6Click(TObject *Sender) { Close(); } //--------------------------------------------------------------------------- Приложение Б (Обязательное) Результаты тестирования программы  Приложение В (Обязательное) Решение задачи в математической системе Mathcad            Изм. Лист № докум. Подп. Дата       Лист И-ПДМз-131.00.ХХХ ПЗ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
