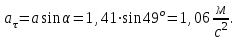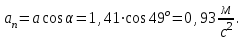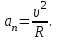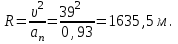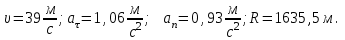задания. Решение Запишем координаты вектора начальной скорости Запишем координаты вектора ускорения
 Скачать 78.59 Kb. Скачать 78.59 Kb.
|
|
Задача 1 Частица движется равноускоренно в координатной плоскости ху с начальной скоростью 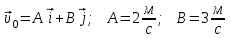 и ускорением и ускорением 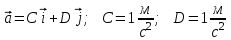 . Найти модули векторов скорости . Найти модули векторов скорости 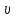 , тангенциального , тангенциального 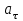 и нормального и нормального 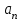 ускорений, а также радиус кривизны R траектории в момент времени ускорений, а также радиус кривизны R траектории в момент времени 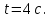
Задача 3 Шар массой m1 , летящий со скоростью 1 v , сталкивается с неподвижным шаром массой m2 . После удара шары разлетаются под углом α друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров 1 u и 2 u после удара. 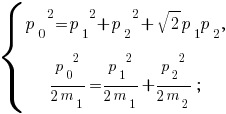 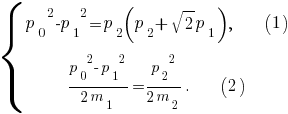 Разделив почленно уравнение (2) на уравнение (1), после преобразований получим 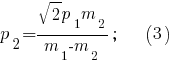 из уравнения (2) с учётом выражения (3) получим 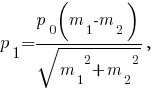 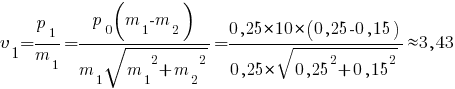 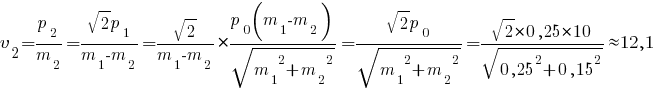 | |||||

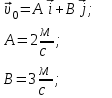
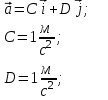
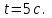
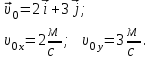
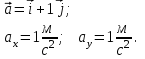
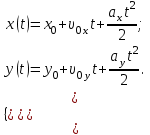
 . После подстановки соответственных значений, получаем:
. После подстановки соответственных значений, получаем: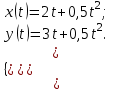
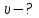
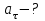
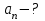
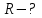
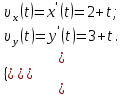
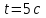 , получаем:
, получаем: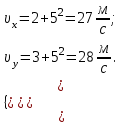
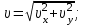
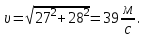
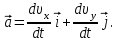
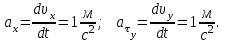
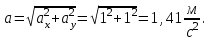
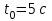 , вычисляется по формуле:
, вычисляется по формуле: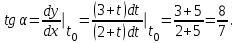
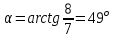 .
.