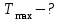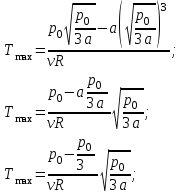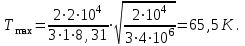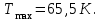Вариант 3
Задание 4
Задача 1
В сосуде объемом 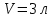 при температуре при температуре 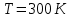 находится смесь двух идеальных газов с массами находится смесь двух идеальных газов с массами 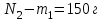 и и 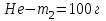 . Найти давление смеси р, молярную массу смеси M и число молекул в N сосуде. . Найти давление смеси р, молярную массу смеси M и число молекул в N сосуде.
Дано:
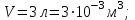
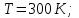

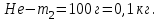
|
Решение:
Запишем уравнение Менделеева – Клапейрона для каждого из двух газов:
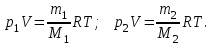
Вычисляем парциальные давление каждого газа:
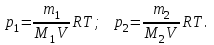
По закону Дальтона, получаем:
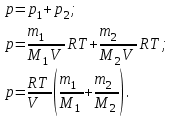
Где 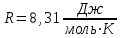 - универсальная газовая постоянная, - универсальная газовая постоянная, 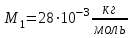 - молярная масса азота, - молярная масса азота, 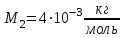 - молярная масса гелия. - молярная масса гелия.
Подставим численные значения и вычислим:
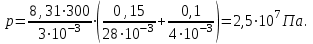
Перепишем последнее уравнение в виде:
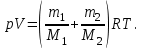 (1) (1)
Запишем уравнение Менделеева – Клапейрона для смеси газов:
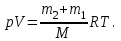 (2) (2)
Приравнивая (1) и (2), получаем:
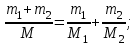
|
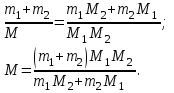
Подставим численные значения и вычислим молярную массу смеси газов:
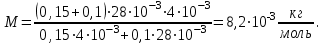
Определим число молекул каждого газа:
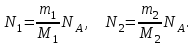
Тогда число молекул в N сосуде будет:
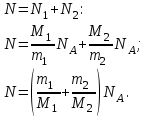
Где 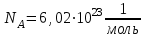 - число Авогадро. - число Авогадро.
Подставим численные значения и произведём вычисления:
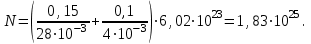
Ответ: 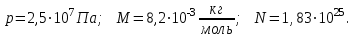
|
Задача 2
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате изохорного 1-2 и изобарного 2-3 процессов. Значения давления и объёма газа в состояниях 1 и 3 равны соответственно  , , 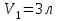 и и 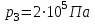 , , 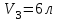 . Найти давление, объём и температуру газа . Найти давление, объём и температуру газа 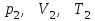 в промежуточном состоянии 2. Изобразить процессы в координатах P - V, P - T и V - T. в промежуточном состоянии 2. Изобразить процессы в координатах P - V, P - T и V - T.
Дано:
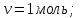
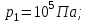
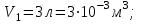

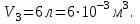
|
Решение:
Поскольку процесс 1-2 изохорный, то 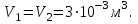
Поскольку процесс 2-3 изобарный, то 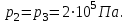
Запишем уравнение Менделеева – Клапейрона для второго состояния газа:
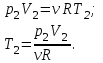
Где 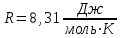 - универсальная газовая постоянная. - универсальная газовая постоянная.
Подставим численные значения и произведём вычисления:
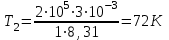
Для состояния 1 запишем уравнение Менделеева – Клапейрона:
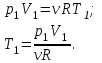
Подставим численные значения и произведём вычисления:
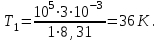
Для состояния 3 запишем уравнение Менделеева – Клапейрона:
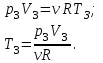
Подставим численные значения и произведём вычисления:
|
Найти:

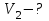
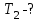
Изобразить:
P - V
P - T
V - T
|
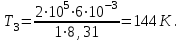
Для построения графиков процессов запишем параметры газа в каждой точке.
В 1-й точке - 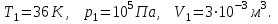
Во 2-й точке - 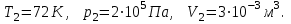
В 3- й точке - 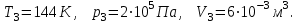
Изобразим процесс в координатах P – V.
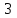
Изобразим процесс в координатах P – Т.
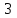
Изобразим процесс в координатах V – Т.
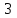
О твет: твет: 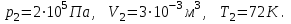
|
Задача 3
Один моль идеального газа совершает процесс, в котором давление газа р убывает с увеличением его объема V по заданному закону 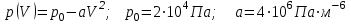 . Найти максимальную температуру газа в этом процессе. . Найти максимальную температуру газа в этом процессе.
Дано:
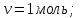
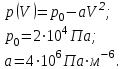
|
Решение:
Запишем уравнение Менделеева – Клапейрона:
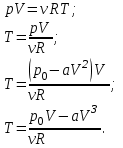
Где 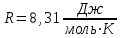 - универсальная газовая постоянная. - универсальная газовая постоянная.
Исследуем функцию 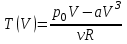 на максимум. на максимум.
Для этого вычисляем производную и приравниваем её к нулю.
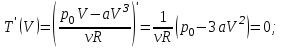
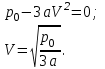
Вычисляем вторую производную:
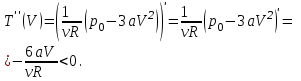
Следовательно при 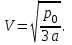 температура максимальна. температура максимальна.
|
Найти:
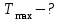
|
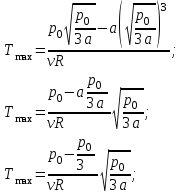

Подставим численные значения и произведём вычисления:
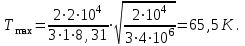
Ответ: 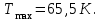
| |
 Скачать 147.31 Kb.
Скачать 147.31 Kb.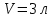 при температуре
при температуре 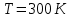 находится смесь двух идеальных газов с массами
находится смесь двух идеальных газов с массами 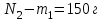 и
и 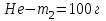 . Найти давление смеси р, молярную массу смеси M и число молекул в N сосуде.
. Найти давление смеси р, молярную массу смеси M и число молекул в N сосуде. ,
, 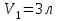 и
и 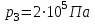 ,
, 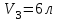 . Найти давление, объём и температуру газа
. Найти давление, объём и температуру газа 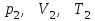 в промежуточном состоянии 2. Изобразить процессы в координатах P - V, P - T и V - T.
в промежуточном состоянии 2. Изобразить процессы в координатах P - V, P - T и V - T.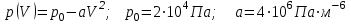 . Найти максимальную температуру газа в этом процессе.
. Найти максимальную температуру газа в этом процессе.
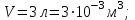
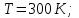

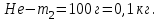
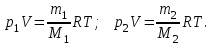
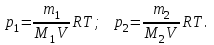
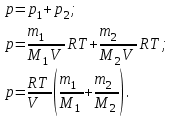
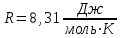 - универсальная газовая постоянная,
- универсальная газовая постоянная, 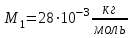 - молярная масса азота,
- молярная масса азота, 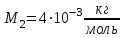 - молярная масса гелия.
- молярная масса гелия.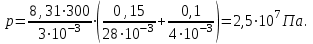
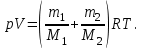 (1)
(1)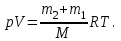 (2)
(2)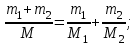
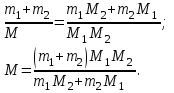
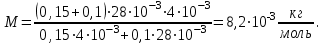
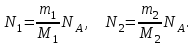
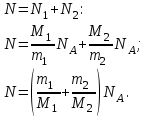
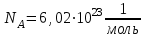 - число Авогадро.
- число Авогадро.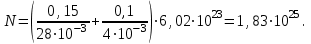
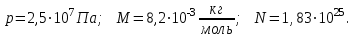
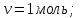
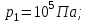
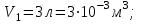

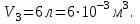
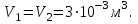
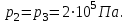
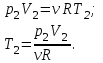
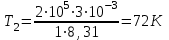
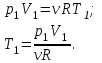
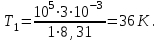
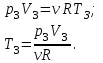

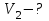
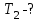
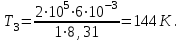
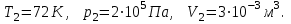
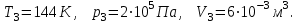
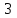
 твет:
твет: 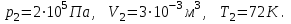
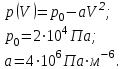
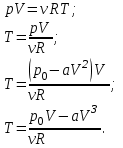
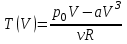 на максимум.
на максимум.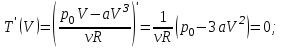
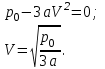
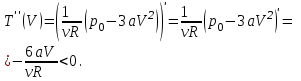
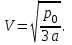 температура максимальна.
температура максимальна.