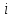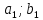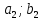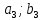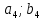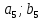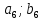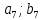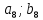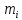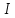Решение Заполним статистический (интервальный) ряд, используя значения
 Скачать 68.45 Kb. Скачать 68.45 Kb.
|
|
Результаты измерений некоторой физической величины представлены в таблице:
где 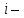 номер интервала, номер интервала, 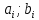 – границы интервала, – границы интервала, 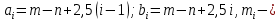 частота. частота.m=6 n=6 Найти функцию распределения выборки 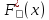 и построить ее график. и построить ее график.Построить гистограмму относительных частот. Найти числовые характеристики выборки: выборочное среднее 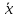 и исправленную выборочную дисперсию и исправленную выборочную дисперсию 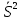 . .Решение Заполним статистический (интервальный) ряд, используя значения 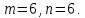
Объем выборки 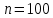 , длина интервала , длина интервала 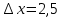 . . Внесем в таблицу дополнительные значения: середины интервалов 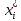 , относительные частоты , относительные частоты 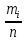 , накопленные относительные частоты , накопленные относительные частоты 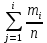 , плотность относительных частот , плотность относительных частот 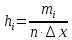 . .
Найдем эмпирическую функцию распределения 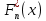 по значениям накопленных относительных частот по значениям накопленных относительных частот 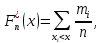 , где , где 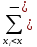 число вариант, меньших x. число вариант, меньших x. Аналитическое выражение эмпирической функции распределения для дискретной случайной величины имеет вид: 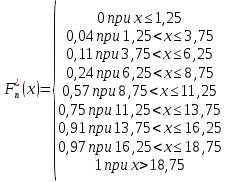 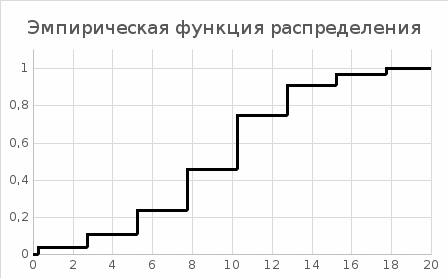 Построим гистограмму относительных частот. На графике по горизонтальной оси ОX отложим частичные интервалы для признака X, а по вертикальной оси ОY –значения плотности относительной частоты 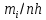 . .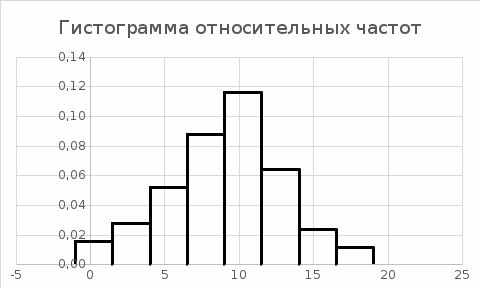  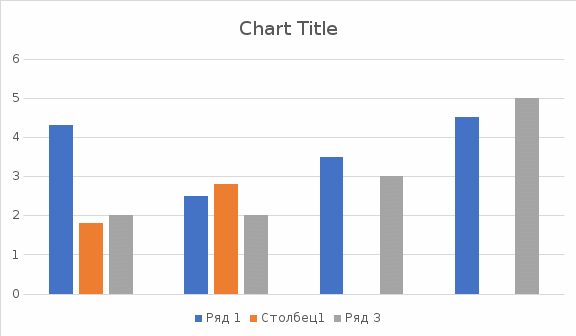 Найдем числовые характеристики выборки. Выборочное среднее 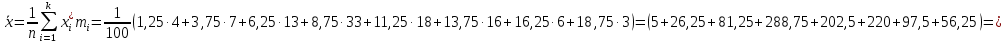 =9,775. =9,775.Исправленная выборочная дисперсия 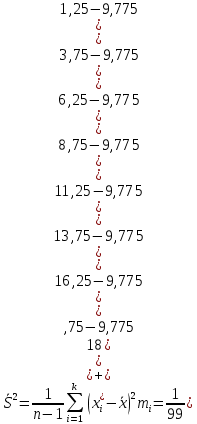 = 18,1433080808. = 18,1433080808. |