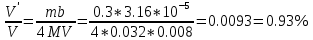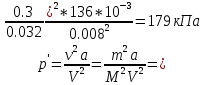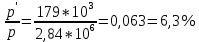Пав. физ1. Решение Зависимость пути s 1 от времени Зависимость пути s 2 от времени
 Скачать 132.23 Kb. Скачать 132.23 Kb.
|
|
100. Расстояние между двумя станциями метрополитена l = 1,5 км. Первую половину этого расстояния поезд проходит равноускоренно, вторую - равнозамедленно с тем же по модулю ускорением. Максимальная скорость поезда v = 54 км/ч. Найти ускорение a и время t движения поезда.
Решение:  Зависимость пути S1 от времени 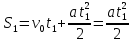 Зависимость пути S2 от времени  Максимальная скорость определяется формулой: 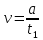 Тогда  Аналогично для второго участка 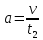 Тогда поскольку а1 = а2, то  и и  Все расстояние l:  Отсюда  Время движения поезда между станциями: 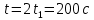 Зная время, найдем ускорение по формуле, записанной ранее: 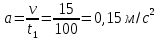 Ответ: t = 200 c, а = 0,15 м/с2 110. С башни высотой h = 25 м горизонтально брошен камень со скоростью v = 15 м/с. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадёт на землю? С какой скоростью v он упадёт на землю?
Решение:  Движение тела, брошенного горизонтально с высоты h, можно разложить на две состаляющих: равномерное движение в горизонтальном направлении вдоль оси х, и равноускоренное движение с нулевой начальной скоростью в вертикальном направлении с ускорением свободного падения g. Для равноускоренного движения с нулевой начальной скоростью можем записать:  Отсюда время падения тела с высоты h: 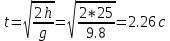 Для равномерного движения в горизонтальном направлении вдоль оси х: тело упадет на расстоянии l от основания башни: 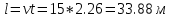 При падении камень будет иметь две составляющие скорости: не меняющуюся v=vx и vy = gt. Результирующее значение скорости находим по формуле: 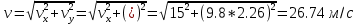 Ответ:  120. Невесомый блок укреплен на конце стола. Грузы соединены нитью и перекинуты через блок таким образом, что один груз расположен горизонтально, а второй – вертикально. Массы грузов m1 = m2 = 1 кг. Коэффициент трения первого груза k = 0,1. Найти ускорение a, с которым движутся грузы, и силе натяжения нити Т. Трением в блоке пренебречь
Решение:  Запишем второй закон Ньютона и его проекции на оси Ох и Оу: Для груза m1: 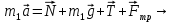 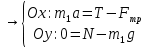 Из второго уравнения системы имеем: 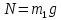 Сила трения определяется формулой:  Тогда  Для груза m2: 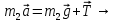 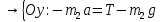 Теперь имеем систему двух уравнений с двумя неизвестными:    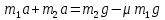   Подставим найденное выражение для ускорения в уравнение (*):  Ответ: 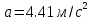 , ,  130. Человек стоит на скамье Жуковского и ловит рукой мяч массой m = 0,4 кг, летящий в горизонтальном направлении со скоростью V = 20 м/c. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начинает вращаться скамья с человеком, поймавшим мяч, если суммарный момент инерции человека и скамьи равен J = 6 кг•м2?
Решение: Мяч обладает моментом импульса относительно оси вращения 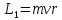 где m – масса мяча, v - скорость мяча, r – расстояние от вертикальной оси вращения скамьи до мяча. Запишем выражение для момента импульса человека со скамьей и мячом:  где J – момент инерции человека со скамьей,  - момент инерции мяча, который равен: - момент инерции мяча, который равен: Тогда 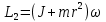 По закону сохранения импульса: 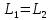 или  Выразим отсюда искомую величину:  Ответ:  140. В сосуде находится масса m1 = 14 г азота и масса m2 = 9 г водорода при температуре t = 127 °С и давлении p = 1 МПа. Найти молярную массу M смеси и объем V сосуда
Решение: Масса газа То же справедливо и для количества вещества Молярная масса определяется формулой:  Тогда 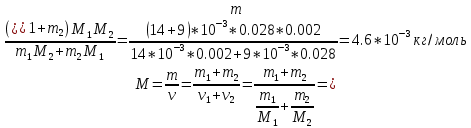 Уравнение Менделеева – Клапейрона 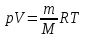 где R – универсальная газовая постоянная Отсюда объем газа 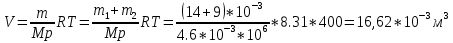 Ответ:  150. Азот массой m = 1 кг занимает при температуре T1 = 300 К объем V1 = 3 л. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определите: 1) конечный объем газа V2; 2) его конечную температуру T2; 3) изменение внутренней энергии газа 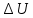
Решение: 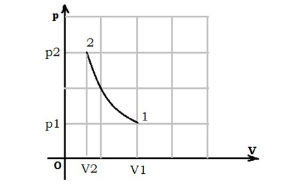 Для адиабатного процесса справедливо равенство: 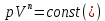 или  n – показатель адиабаты, который равен:  i – число степеней свободы газа Отсюда можно найти конечный объем:  Теперь определим конечную температуру. Из уравнения Менделеева-Клапейрона: 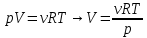 C учетом (*) получим:    Преобразуем дальше 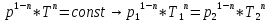 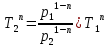 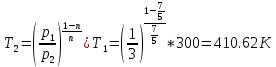 Внутренняя энергия определяется формулой:  Ответ:  160. Воду массой m = 1 г нагрели от температуры t1 = 10  до температуры t2 100 до температуры t2 100  , при которой она вся испарилась. Найти , при которой она вся испарилась. Найти 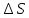 приращение энтропии системы. приращение энтропии системы.
Решение:Рассмотрим изменение энтропии при нагревании воды от t1 до t2 и при испарении воды. 1. Нагревание воды от t1 lдо t2 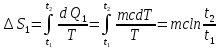 2. Испарение воды при температуре t2  Результирующее изменение энтропии 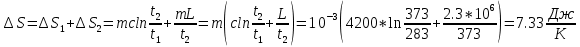 Ответ:  170. В баллоне вместимостью V=8 л находится кислород массой m=0,3 кг при температуре T=300 К. Найти, какую часть вместимости сосуда составляет собственный объем молекул газа. Определить отношение внутреннего давления p' к давлению p газа на стенки сосуда.
Решение:Собственный объем молекул найдем, воспользовавшись постоянной b Ван-дер-Ваальса, равной учетверенному объему молекул, содержащихся в одном моле реального газа. В уравнении Ван-дер-Вальса |
| Дано: q1 = 10 мкКл = 10*10-6 Кл q2 = -20 мкКл = - 20 *10-6 Кл d = 5 cм = 0,05 м r1 = 2 см = 0,02м r2 = 5 см = 0,05 м q = 1мкКл = 10-6 Кл |
| Найти: Е - ? F - ? |
Решение:
Поле, создаваемое зарядом q1
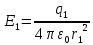
Поле, создаваемое зарядом q2

Результирующее поле определяем по теореме косинусов
где

Тогда



Cилу определим по формуле:

Ответ: Е = 80*106 В/м,

190. Па тонкой нити, изогнутой по дуге окружности радиусом R = 15 см, равномерно распределен заряд q = 10 нКл. Определить напряженность поля E , создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
| Дано: R = 15 см =0,15 м q = 10 нКл = 10*10-9 Кл |
| Найти: Е - ? |
Решение:

Оси координат выбраны так, чтобы начало совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена относительно концов дуги. На нити выделяется элемент длины dl, заряд dq на участке dl можно считать точечным. Напряжённость электрического поля в точке O
 ,
,где
 - радиус-вектор, направленный от элемента dl к точке, напряжённость которой вычисляется.
- радиус-вектор, направленный от элемента dl к точке, напряжённость которой вычисляется. Тогда
 , (3)
, (3)где
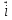 ,
, 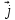 - единичные векторы направлений.
- единичные векторы направлений.Тогда
 . (4)
. (4)Для того чтобы получить выражение для
 , используем равенства (3) и (4), учтём симметричность относительно оси Y, проинтегрируем в пределах
, используем равенства (3) и (4), учтём симметричность относительно оси Y, проинтегрируем в пределах 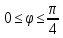 (по построению рисунка) и удвоим результат:
(по построению рисунка) и удвоим результат: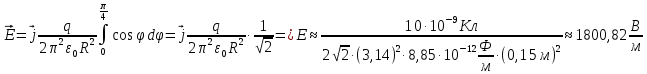 .
.Ответ:
 .
.

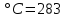 К
К

 означает учетверенный объем молекул всего газа, т.е.
означает учетверенный объем молекул всего газа, т.е.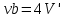


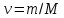 - количество вещества, М – молярная масса
- количество вещества, М – молярная масса