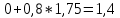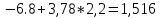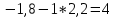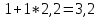Методы оптимизации 2. СементеевАА_МО_ЛР№2. Решение злп симплекс методом по дисциплине Методы оптимизации
 Скачать 34.05 Kb. Скачать 34.05 Kb.
|
|
ФГБОУ ВО Уфимский Государственный Авиационный Технический Университет Кафедра АСУ Отчёт по лабораторной работе №3 «Решение ЗЛП симплекс методом» по дисциплине «Методы оптимизации» Вариант 18. Выполнил: ст. гр. ПИ-221 Сементеев А.А Проверил: ст.пр.кф.асу Кондратьева О.В. Уфа 2021 Цель работы: научиться решать задачи линейного программирования симплекс методом. Ход работы: Задача. При откорме каждое животное должно получать не менее 11 ед. белков, 10 ед. углеводов и 16 ед. протеина. Для составления рациона используют два вида корма, представленных в следующей таблице:  Рисунок 1. Таблица-условие Стоимость 1 кг корма первого вида – 6 д.е., второго – 7 д.е. Составьте дневной рацион питательности, имеющий минимальную стоимость. Идентификация переменных и целевая функция Переменные x отражают количество килограмм корма. Пусть x1 – количество кг корма 1 вида, а x2, соответственного, количество кг 2 вида. Тогда общая стоимость корма будет иметь вид:  Поскольку нам необходимо найти минимальную стоимость, то мы решаем задачу минимизации. Ограничения системы Из условия известна норма потребления питательных веществ животного – это и будет являться нашими ограничениями, а также ограничение на положительность x1 и x2 (не может быть отрицательное количество кг):  Итоговая математическая модель будет иметь следующий вид:   Преобразуем задачу в каноническую форму. Для этого введем доп. переменные x3, x4 и x5. Тогда система ограничений будет выглядеть следующим образом:  Построим исходную симплекс таблицу – столбцами таблицы являются все переменные из мат. модели, а в ячейках записываются коэффициенты при этих переменных. Строки соответствуют ограничениям задач.
Единичной подматрице соответствуют столбцы x3, x4 и x5, т.е. эти переменные являются начальными базисными решениями. 1 Начальное базисное решение x3 = 11, x4 = 10, x5 = 16. Первая итерация Находим генеральный столбец max(6;7) = 7 Найдем генеральную строку min(  ) = 2,75 ) = 2,75Генеральный элемент равен 4. Формирование «новой» строки Базисная переменная в «новой» строке соответствует переменной генерального столбца.
Последняя строка в столбце bj заполняется значением целевой функции F. Базисные переменные x2 = 2,75; x4 = 7,25; x5 = -2,75 F (0;2,25;0;7,25;-2,75) = 6*0 + 7*2,25 + 0*0 + 0*7,25 + 0*(-2,75) = 15,75 Вывод: данное решение не является оптимальным, так как существует оценка коэффициентов ЦФ, которая больше 0. Вторая итерация Найдем генеральный столбец max(0,75;0;1,75;0;0) = 1,75 Найдем генеральную строку min(  ; ; = =  – генеральная строка x5 – генеральная строка x5Генеральный элемент равен 1,25.
F (0;3,2;1,8;-6,8;0) = 6*0 + 7*3,2 = 22,4 Вывод: данное решение не является оптимальным, так как существует оценка коэффициентов ЦФ, которая больше 0. Третья итерация Найдем генеральный столбец – x1 Найдем генеральную строку min( 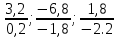 ) = -0,81 ) = -0,81Генеральный элемент равен –2,2
F (3,78;2,44;0;1,516;0;0) = 6*3,78 + 7*2,44 = 39,76 Вывод: данное решение является оптимальным, так как не существует оценка коэффициентов ЦФ, которая больше 0. Оптимальное значение, полученное при решении графическим методом, совпадает с решением симплекс методом. Таким образом, дневной рацион будет состоять из 3,78 кг корма 1 вида и 2,44 кг корма 2 вида. При таких значениях затраты будут минимальны и составят 39,76 денежных единиц. |

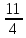 = 2,75
= 2,75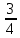 = 0,75
= 0,75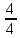 = 1
= 1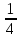 = -0,25
= -0,25 = 0
= 0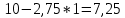
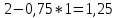
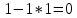


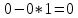
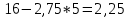


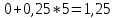
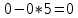
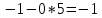
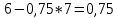

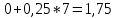
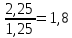
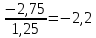
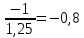
 4,6
4,6