Максвелл теңдеулері. Рэт 417 СЖ 1
 Скачать 34.29 Kb. Скачать 34.29 Kb.
|
|
Кеңесов Ернұр РЭТ – 417 СӨЖ 1 Максвелл теңдеулер жүйесі Интегралдық теңдеулер ғарыштың әр нүктесінде электромагниттік процестер туралы ақпарат алуға мүмкіндік бермейді. Олар кеңістіктегі өрістердің орташа шешімдерін береді. Математикалық шешімдердің жақсы дамыған аппараты интегралдық формадан дифференциалдық шешімдерге өтуге мүмкіндік береді. Максвелл алғаш рет интегралдық теңдеулерден дифференциалдық теңдеулерге көшті. Максвеллдің бірінші теңдеуі: Максвеллдің бірінші теңдеуі - толық ток Заңының дифференциалды тұжырымы: 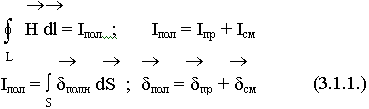 осы формулаларға өзгерту енгізу арқылы: осы формулаларға өзгерту енгізу арқылы: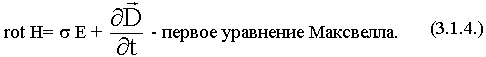 - бірінші Максвелл теңдеуін аламыз. - бірінші Максвелл теңдеуін аламыз. Оның физикалық мағынасы - құйынды магнит өрісінің көзі өткізгіштік және ығысу токтары болып табылады. Максвеллдің екінші теңдеуі: Максвеллдің екінші теңдеуі - электромагниттік индукция заңының дифференциалды тұжырымы: 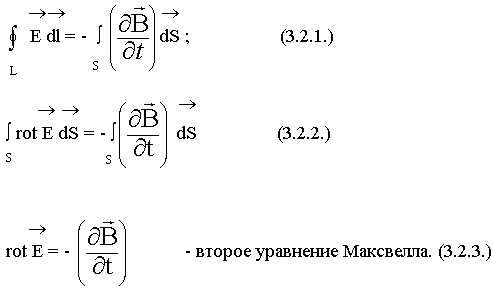 Максвеллдің екінші теңдеуі. Максвеллдің екінші теңдеуі. Физикалық мағынасы: Құйынды электр өрісі ауыспалы магнит өрісі арқылы жасалады. Максвеллдің үшінші теңдеуі: Максвеллдің үшінші теңдеуі-электр өрістеріне арналған Гаусс теоремасының дифференциалды тұжырымы. 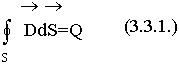 (1) (1) 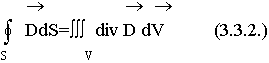 (2) (2)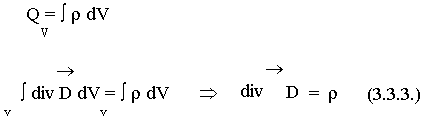 (3) 3 және 2 формулаларды 1 формулаға қойып Үшінші теңдеуді аламыз Физикалық мағынасы: Электр өрісінің көздері (E және D векторлары) ρ тығыздығы бар зарядтар болып табылады . Максвеллдің төртінші теңдеуі Максвеллдің төртінші теңдеуі - магнит өрістеріне арналған Гаусс теоремасының дифференциалды тұжырымы:   - Максвеллдің төртінші теңдеуі - Максвеллдің төртінші теңдеуіФизикалық мағынасы: Кеңістіктің кез - келген нүктесіндегі вектордың дивергенциясы нөлге тең, яғни көздер жоқ (табиғатта магниттік зарядтар жоқ). |
