18-19.Резонансные кривые связанных контуров, ФЧХ. Резонансные кривые связанных контуров
 Скачать 76.04 Kb. Скачать 76.04 Kb.
|
|
Резонансные кривые связанных контуров Основной интерес представляет поведение амплитуд токов в контурах вблизи резонансных частот системы. Для простоты полагаем, что резонансные частоты контуров равны между собой: Полные сопротивления контуров 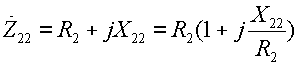 . На частотах близких к резонансной частоте где Ток в первом контуре 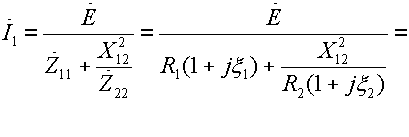 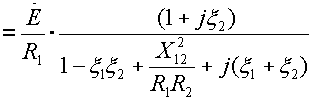 Ток во втором контуре 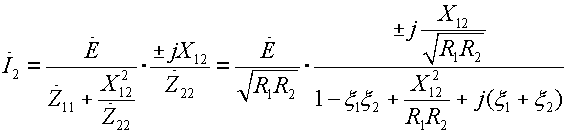 . .На частотах, близких к резонансной частоте 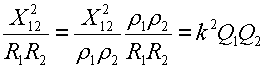 . .Кроме того, выше было получено 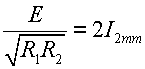 , , 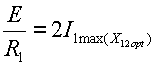 . .Таким образом, подставив последние выражения в формулы для токов, получим уравнения нормированных резонансных кривых первого и второго контуров 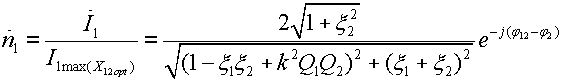 , ,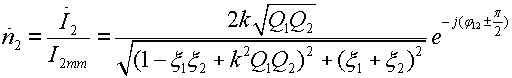 , ,где Для одинаковых контуров, использующихся в полосовых фильтрах приемников, 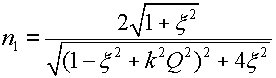 , , 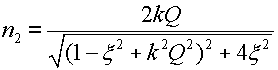 - -- амплитудно-частотные характеристики первого и второго контуров, 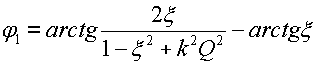 , , - фазочастотные характеристики первого и второго контуров. На рис.80 приведены АЧХ и ФЧХ второго контура в функции обобщенной расстройки при пяти различных значениях произведения kQ. (kQ характеризует степень связи контуров и называется параметром или фактором связи). 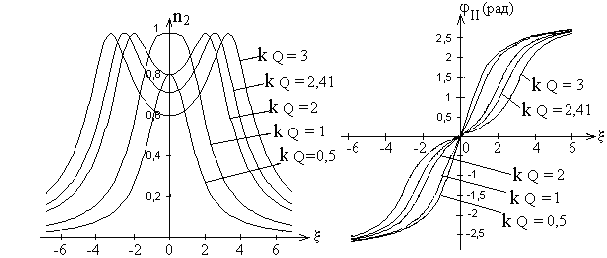 Рис. 80 Из графиков амплитудно-частотной характеристики (рис.80, а) видно, что при факторе связи kQ < 1 кривые имеют одногорбый характер с максимумом на резонансной частоте ( откуда  , ,  . .Фазо-частотная характеристика (рис.80, б), построенная для соответствующих факторов связи, должна быть поднята по оси ординат на Частотные характеристики первого контура (рис.81) изменяются более резко при изменении обобщенной расстройки, чем характеристики второго контура. Это объясняется наличием в выражении для резонансной кривой в числителе множителя, зависящего от величины расстройки (в аналогичном выражении для второго контура числитель от частоты не зависит).  Рис. 81 Таким образом, образование седловины на АЧХ первого контура получается при меньших факторах связи, чем во втором контуре (рис.81, а). Фазо-частотная характеристика (рис.81, б) при факторах связи больше единицы трижды переходит через нуль, что соответствует резонансной частоте ( Если два связанных контура имеют одинаковые резонансные частоты, но разные добротности (  , ,где 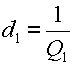 и и 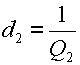 - затухание контуров. - затухание контуров. При этом, частоты связи тем больше отличаются от резонансной частоты, чем больше коэффициент связи отличается от критического 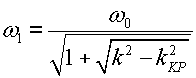 , , 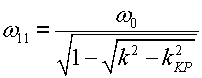 . . |
