Статья. 6_Прик механика. Результаты расчета полубесконечной балки на двухпараметрическом основании с особенностью в основании
 Скачать 345.79 Kb. Скачать 345.79 Kb.
|
|
Известия КГТУ им. И.Раззакова 63/2022 ПРИКЛАДНАЯ МЕХАНИКА. МАТЕМАТИКА И ФИЗИКА УДК 624.073.02 РЕЗУЛЬТАТЫ РАСЧЕТА ПОЛУБЕСКОНЕЧНОЙ БАЛКИ НА ДВУХПАРАМЕТРИЧЕСКОМ ОСНОВАНИИ С ОСОБЕННОСТЬЮ В ОСНОВАНИИ Маруфий Адылжан Таджимухамедович, доктор технический наук, профессор, Ошский технологический университет им. М. Адышева, Ош, Кыргызстан, e-mail: oshtu-marufi@rambler.ru Калыков Абдижалил Сагынбаевич, главный специалист, Государственный институт сейсмостойкого строительства и инженерного проектирования, Бишкек, Кыргызстан,e-mail: dzhalil_8@mail.ru Турдажиева Эльнура Номановна, ст. преподаватель, Ошский технологический университет им. М. Адышева, Ош, Кыргызстан,e-mail: turdazhiyeva@inbox.ru Аннотация. В данной статье произведена численная реализация задачи изгиба полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении от края полубесконечной балки на основе ранее полученного аналитического решения методом обобщенных решений с использованием интегральных преобразований Фурье. Произведен подробный анализ полученных результатов. Ключевые слова: метод обобщенных решений, преобразование Фурье, упругое основание, изгиб. THE RESULTS OF THE CALCULATION OF A SEMI-INFINITE BEAM ON A TWO-PARAMETER BASE WITH A SINGULARITY IN THE BASE Marufi Adilzhan Tajimuhammedovich, doctor of Technical Sciences, professor, OshTU , Osh, Kyrgyzstan, e-mail: oshtu-marufi@rambler.ru Kalykov Abdizhalil Sagynbaevish, cheer specialist, State Institute of Earthquake Engineering and engineering design, Bishkek, Kyrgyzstan, e-mail: dzhalil_8@mail.ru Turdazhieva Elnura Nomanovna, senior lecturer, OshTU, Osh, Kyrgyzstan, e-mail: turdazhiyeva@inbox.ru THE RESULTS OF THE CALCULATION OF A SEMI-INFINITE BEAM ON A TWO-PARAMETER BASE WITH A SINGULARITY IN THE BASE Abstract. This article discusses the numerical implementation of the problem of bending a semi-infinite beam on a two-parameter elastic base with regard to incomplete contact with the base in the form of a trench located at a distance from the edge of the semi-infinite beam based on previously obtained analytical solutions using the method of generalized solutions using Fourier integral transforms. Produced a detailed analysis of the results. Key words: generalized solution method, Fourier transform, elastic base, bending. Введение. При проектировании ленточных фундаментов зданий и сооружений, опирающихся на грунт в виде лессовых отложений необходимо учитывать, что под балкой при замачивании этих просадочных грунтов может образоваться провал (неполный контакт основания). Расположение отверстия (неполного контакта) в основании может быть в различных местах конструкций фундаментов: в центре, вблизи края. Цель исследования. Численная реализация ранее полученного аналитического решения задачи об изгибе полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении от края полубесконечной балки. Метод исследования. Составление и отладка программы расчета в среде Delphi и вывод графиков с помощью системы AutoCAD. В работе [1] получено точное аналитическое решение задачи изгиба полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной под балкой шириной 2а на удлинении b от края полубесконечной балки (рис.1) на основе метода обобщенных решений с использованием интегральных преобразований Фурье. 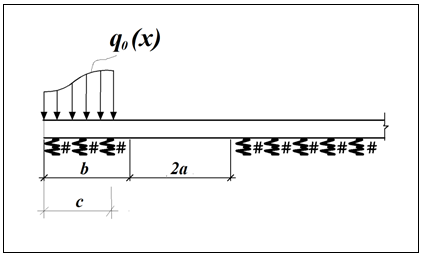 Рис.1 Полубесконечная балка на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки В этом случае исходное дифференциальное уравнение изгиба полубесконечной балки в безразмерных координатах и функциях имеет вид [2,3,4,5]: 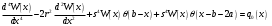 (1) (1)Применяя прямое и обратное cos-преобразование Фурье к выражению (1), получим интегральное уравнение [6,7]: 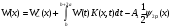 (2) (2)В формуле (2) 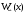 - прогиб в бесконечной балке, условно полностью лежащей на упругом двухпараметрическом основании и загруженной нагрузкой на заданной и дополнительной частях балки. - прогиб в бесконечной балке, условно полностью лежащей на упругом двухпараметрическом основании и загруженной нагрузкой на заданной и дополнительной частях балки.Решение интегрального уравнения (2) приведено в [1], таким образом, значения прогибов, углов поворота, изгибающих моментов и поперечных сил для балки (рис.2) загруженной силой Р на краю полубесконечной балки имеют вид: 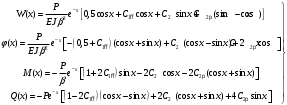 (3) (3)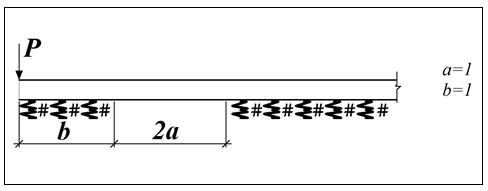 Рис.2 Полубесконечная балка на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки, загруженной на краю балки силой Р При действии равномерно распределенной нагрузки на участке балки 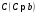 (рис.3) прогиб балки имеет вид: (рис.3) прогиб балки имеет вид: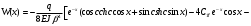 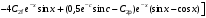 На оставшемся участке балки при 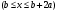 из (7) и [1] следует: из (7) и [1] следует: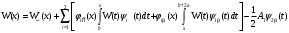 (4) (4)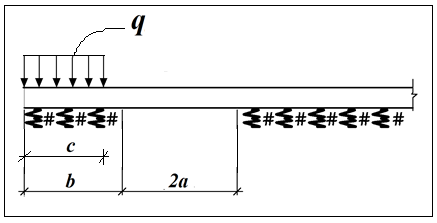 Рис.3 Полубесконечная балка на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки, загруженной на краю балки равномерно распределенной нагрузкой Для определения прогибов в различных точках этого интервала разделим его на n частей и заменим интегралы конечными суммами. Тогда, прогиб в точке 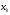 имеет вид: имеет вид: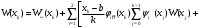 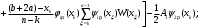 (5) (5)Давая параметру 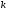 различные значения, получим систему уравнений, из решения которой определим искомое значение прогиба различные значения, получим систему уравнений, из решения которой определим искомое значение прогиба 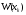 . .Для вычисления значений 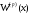 в различных точках делим интервал в различных точках делим интервал 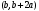 на n частей. В результате, получим: на n частей. В результате, получим: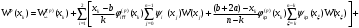 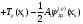 (6) (6)Давая параметру k различные значения 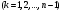 , получим систему уравнений для определения значений прогибов , получим систему уравнений для определения значений прогибов 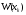 . В правую часть этой системы входят функции . В правую часть этой системы входят функции 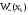 , определяемые для сосредоточенной силы по формуле [8], а для распределенной нагрузки также по формулам [8] в зависимости от положения точки , определяемые для сосредоточенной силы по формуле [8], а для распределенной нагрузки также по формулам [8] в зависимости от положения точки 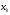 . . В качестве примера рассмотрим задачу изгиба полубесконечной балки, нагруженной на краю сосредоточенной силой и имеющей на приведенном расстоянии 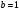 участок балки, не контактирующей с основанием размером участок балки, не контактирующей с основанием размером 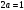 или или 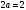 . Соответствующие эпюры показаны на рис.4 и рис.5, на них пунктиром показаны значения прогибов, изгибающих моментов для полубесконечной балки, полностью контактирующей с основанием. Здесь также, как и в бесконечной балке наличие участка основания . Соответствующие эпюры показаны на рис.4 и рис.5, на них пунктиром показаны значения прогибов, изгибающих моментов для полубесконечной балки, полностью контактирующей с основанием. Здесь также, как и в бесконечной балке наличие участка основания 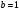 приводит к незначительным различиям в значениях эпюр. приводит к незначительным различиям в значениях эпюр.Если уменьшить участок 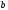 , например, приняв , например, приняв 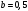 , то это различие увеличивается (рис.6). , то это различие увеличивается (рис.6).На основании изложенного в [1] алгоритма точного аналитического решения задачи изгиба полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении от края полубесконечной балки составлена программа в среде Delphi, а вывод графиков осуществлен в системе AutoCAD [9,10]. Результаты численной реализации приведены на рис.4, 5, 6 и в таблицах 1,2 и 3. 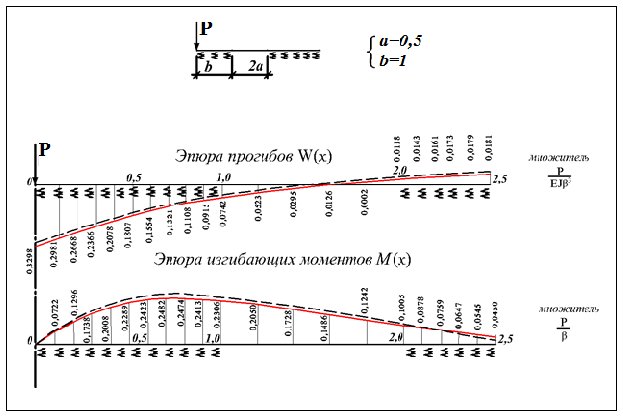 Рис.4 Эпюра прогибов W(x), изгибающих моментов M(x) при а=0,5 иb=1 полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки Таблица 1- Значения прогибов W(x) и изгибающих моментов M(x) при а=0,5 и b=1 полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки
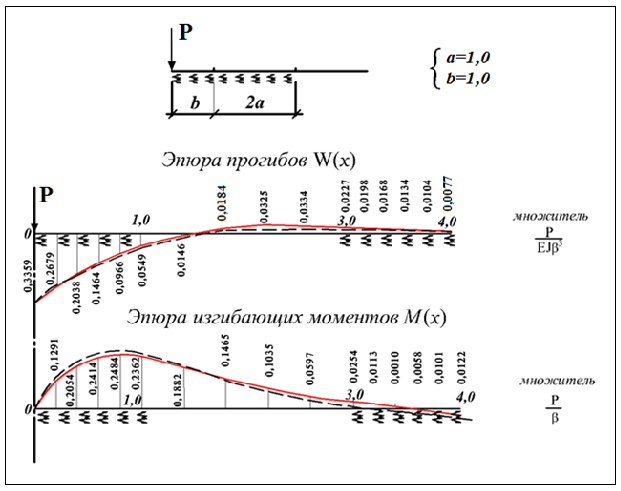 Рис.5 Эпюра прогибов W(x), изгибающих моментов M(x) при а=1,0 иb=1,0 полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки. Таблица 2 - Значения прогибов W(x) и изгибающих моментов M(x) при а=1,0 иb=1,0 бесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки.
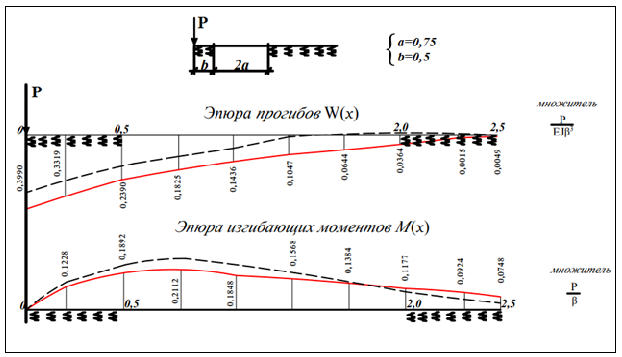 Рис.6 Эпюра прогибов W(x), изгибающих моментов M(x) при а=0,75 иb=0,5 полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки. Таблица 3- Значения прогибов W(x) и изгибающих моментов M(x) при а=0,75 иb=0,5 полубесконечной балки на двухпараметрическом упругом основании с учетом неполного контакта с основанием в виде траншеи, расположенной на удалении b от края полубесконечной балки.
Выводы: В статье произведена численная реализация ранее полученного авторами аналитического решения. Результаты расчета показывают, что максимальный прогиб при параметрах 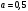 и и 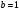 в 1,54 раза меньше в случае использования двухпараметрической модели (0,3298), чем модели Винклера (0,5079), а максимальный изгибающий момент, при двухпараметрической модели (0,2482), а по модели Винклера (0,3102), т.е. в 1,25 раза меньше. При параметрах в 1,54 раза меньше в случае использования двухпараметрической модели (0,3298), чем модели Винклера (0,5079), а максимальный изгибающий момент, при двухпараметрической модели (0,2482), а по модели Винклера (0,3102), т.е. в 1,25 раза меньше. При параметрах 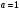 и и 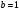 при двухпараметрической модели максимальные прогибы равны 0,3359, а по модели Винклера 0,5174, т.е. также в 1,54 раза, а максимальные изгибающие моменты при двухпараметрической модели равен 0,2484, а по модели Винклера равен 0,3105 также в 1,25 раза. При параметрах при двухпараметрической модели максимальные прогибы равны 0,3359, а по модели Винклера 0,5174, т.е. также в 1,54 раза, а максимальные изгибающие моменты при двухпараметрической модели равен 0,2484, а по модели Винклера равен 0,3105 также в 1,25 раза. При параметрах 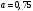 и и 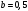 максимальные прогибы при двухпараметрической модели равны 0,3990, а по модели Винклера 0,6145, т.е. в 1,54 раз меньше. Максимальный изгибающий момент при двухпараметрической модели равен 0,2112, а по модели Винклера равен 0,2640 в 1,25 раза меньше при действии сосредоточенной силы максимальные прогибы при двухпараметрической модели равны 0,3990, а по модели Винклера 0,6145, т.е. в 1,54 раз меньше. Максимальный изгибающий момент при двухпараметрической модели равен 0,2112, а по модели Винклера равен 0,2640 в 1,25 раза меньше при действии сосредоточенной силы 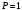 на краю полубесконечной балки. на краю полубесконечной балки.Список литературы: Маруфий А.Т. Алгоритм расчета полубесконечной балки на двухпараметрическом упругом основании с участком без основания на удалении от края под балкой [Текст]/А.Т. Маруфий, А.А. Эгенбердиева/ Известия КГТУ №3(51), 2019.-126-133с. Маруфий, А.Т. Изгиб полубесконечной балки на двухпараметрическом упругом основании с неполным контактом с основанием на краю балки [Текст]/А.Т. Маруфий, А.А. Эгенбердиева/ Вестник КГУСТА №1 (63), Бишкек, 2019.-59-64с. Травуш, В.И. Метод обобщенных решений в задачах изгиба плит на линейно-деформируемом основании [Текст]/ В.И. Травуш. – Строительная механика и расчет сооружений №1, 1982.‒24-28 с. Маруфий, А.Т. Расчет плит на упругом основании при отсутствии основания под частью плиты [Текст]/ А.Т. Маруфий. – «Основания, фундаменты и механика грунтов» №4,1999. –27-31с. Маруфий, А.Т. Изгиб различных схем плит на упругом основании с учетом неполного контакта с основанием [Текст]/ А.Т. Маруфий. – М.: Издательство АСВ, СНГ, 2003. –206с. Травуш, В.И. Влияние локального увлажнения лессовых грунтов на перераспределение реактивных отпоров под фундаментами / В.И. Травуш, А.Т. Маруфий, А.В. Цой// Основание, фундаменты и механика грунтов, 2016. -№2.–2-4с. Травуш В.И. Об одном методе решения задач изгиба конструкций, лежащих на винклеровском основании [Текст]/В.И. Травуш// Сб. трудов «Вопросы архитектуры и строительства зданий для зрелищ, спорта и учреждений культуры».- М.- 1976.- №4. –С. 83-89 Маруфий, А.Т. Изгиб бесконечной балки на двухпараметрическом упругом основании с одним участком неполного контакта с основанием [Текст]/А.Т. Маруфий, Э.С. Рысбекова и А.А. Эгенбердиева/ Вестник КГУСТА №1, Бишкек.‒2016.‒ 252-256 с. Чертик А.А. Программирование в среде Delphi [Текст] / А. А.Чертик. – СПб: Питер, 2008. –400с. Соколова Т. Ю. AutoCAD – 2008 [Текст] / Т. Ю. Соколова. – СПб: Питер, 2008 ПРИКЛАДНАЯ МЕХАНИКА, МАТЕМАТИКА И ФИЗИКА |
