Практическое задание. Практическая работа. Российский государственный социальный университет практическое задание 4 по дисциплине Алгоритмы и структуры данных

• Название: Российский государственный социальный университет практическое задание 4 по дисциплине Алгоритмы и структуры данных
• Анкор: Практическое задание
• Дата: 26.11.2022
• Размер: 318.3 Kb.
• Имя файла: Практическая работа.docx
• Тип: Документы; #813985

Российский государственный социальный университет

ПРАКТИЧЕСКОЕ ЗАДАНИЕ №4

по дисциплине «Алгоритмы и структуры данных»
Алгоритмы поиска в массивах

(тема практического задания)

ФИО студента	Давыдов Марк Евгеньевич
Направление подготовки	Программная инженерия
Группа	ПИН-Б-0-Д-2021-2

Москва

Вариант 5

Фибоначчиев поиск.
Принцип работы алгоритма:

1) Последовательность сортируется в возрастающем порядке. Если последовательность уже отсортирована, то этот пункт можно пропустить.

2) Производится начальная инициализация. Нужно найти такое число k, что F(k+1) >= N+1. После чего нужно ввести следующие значения. M = F(k+1)-(N+1), i = F(k)-M, p = F(k-1), q = F(k-2).

3) проверить корректность индекса. Если индекс меньше нуля, перейти к пункту 5. Если индекс больше или равен N, то перейти к пункту 4. Выполнить сравнение K < K_i, если да, то перейти к пункту 4. Если K > K_i, перейти к пункту 5. K = K_i вернуть i, поиск успешен.

4) Выполнить проверку q = 0. Если да, поиск неудачен, закончить выполнение. В противном случае, установить:

i = i – q

выполнить обмен (p, q) = (q, p – q)

Перейти к пункту 3.

5) Выполнить проверку p = 1. Если да, поиск неудачен, закончить выполнение. В противном случае, установить:

i = i + q

p = p – q

q = q – p

Перейти к пункту 3.

Тут N – число элементов в последовательности. К – искомый элемент. K_i – элемент последовательности, расположенный на i – индексе. F(k) – k – й элемент последовательности Фибоначчи.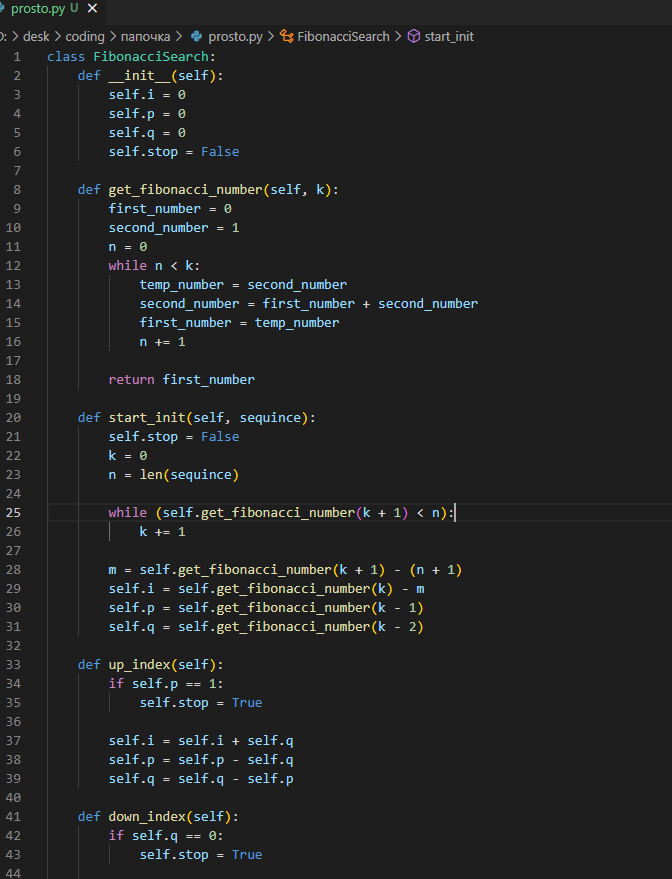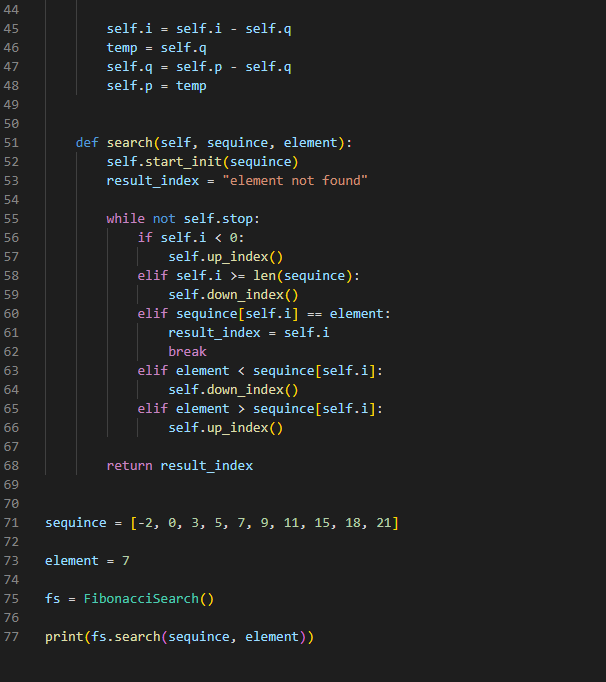



Когда мы ищем элемент, который существует в массиве, то в ответ нам возвращается значение его индекса. (под которым он находится в массиве)





Иначе (‘element not found').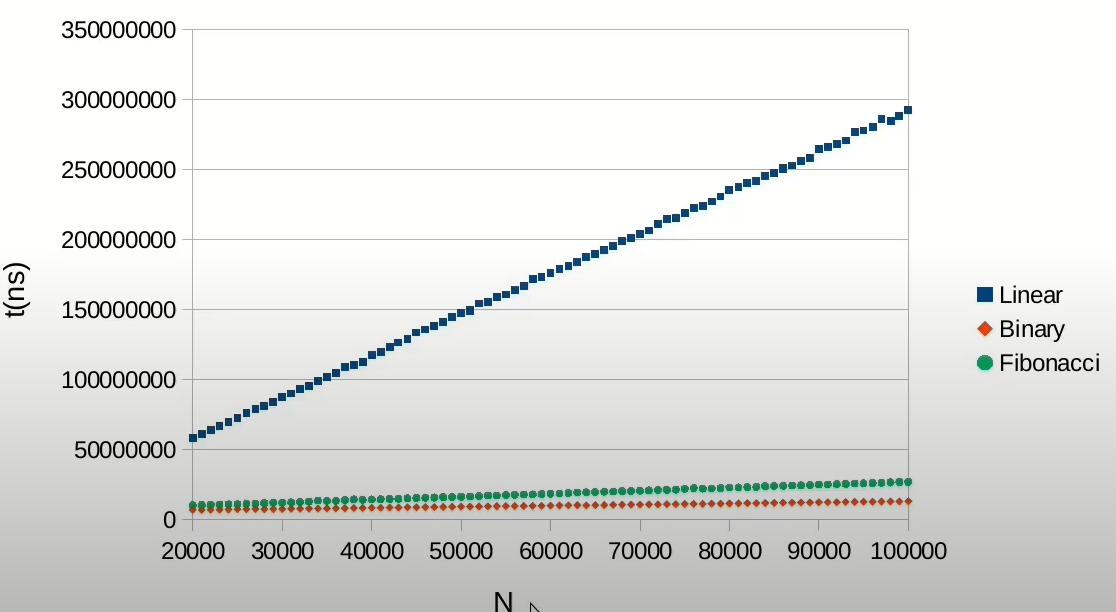





Был проведен эксперимент, чтобы выяснить какой алгоритм быстрее. Бинарный поиск оказался самым быстрым. Именно по этой причине, он чаще всего и используется. Хотя, как можно заметить, что Фибоначчиев поиск не так уж и медленный, по сравнению с бинарным поиском. Но все же медленнее. Тогда возникает вопрос. А для чего вообще нужен Фибоначчиев поиск? В отличии от бинарного поиска, этот алгоритм не имеет операций делений в своем коде. А как мы знаем, не все базовые вычислительные архитектуры поддерживают операцию деления. Так что с этим алгоритмом вы можете обойтись только одной операцией, операцией сложения.