Исаков Б.В. Математика_ П33. Российский государственный социальный университет практическое задание 2 по дисциплине Математика

• Название: Российский государственный социальный университет практическое задание 2 по дисциплине Математика
• Дата: 16.06.2022
• Размер: 91.1 Kb.
• Имя файла: Исаков Б.В. Математика_ П33.docx
• Тип: Документы; #596446

Российский государственный социальный университет

ПРАКТИЧЕСКОЕ ЗАДАНИЕ 2

по дисциплине «Математика»

ФИО студента	Исаков Брендон Владимир оглы
Направление подготовки	38.03.01 «Экономика (бакалавр)
Группа	ЭКН-Б-0-З-2019-1

Москва 2022

1. 
   Определить верхнюю и нижнюю цены игра, оптимальную стратегию и если возможно, седловую точку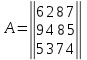
   

α₁ = min (6, 2, 8, 7) = 2 α₂ = min (9, 4, 8, 7) = 4

α₃ = min (5, 3, 7, 4) = 3 α = max (α₁, α₂ , α₃) = α₂ = 4

β₁ = max (6, 9, 5) = 9 β ₂ = max (2, 4, 3) = 4

β₃ = max (8, 8, 7) = 8 β₄= max (7, 5 , 4) = 7

β = min (β₁, β₂ , β_3, β₄) = β₂ = 4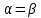

– Седлавая точка (2; 2)

Оптимальная стратегия: I игрока

( 9 4 8 5)

(А_2, В₂) II игрока

( 2 4 3)

2. 
   Определить верхнюю и нижнюю цены игра, оптимальную стратегию и если возможно, седловую точку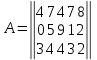
   

α₁ = min (4, -7, -4, 7, 8) = -7

α₂ = min (0, 5, 9, 1, 2) = 0

α₃ = min (3, 4, 4, -3, -2) = -3

α = max (-7, 0, -3) = α_{2 =} 0

β₁ = max (4, 0, 3) = 4 β ₂ = max (-7, 5, 4) = 5

β₃ = max (-4, 9, 4) = 9 β₄ = max (7, 1, -3) = 7

β₅ = max (8,2, -2) = 8 β = min (β₁, β₂ , β_3, β_4, β₅) = β₁ = 4

α ≠ β Седловой точки нет

0 ≤ υ ≤ 4, υ – цена игры

3. 
   Решить игру в смешанных стратегиях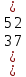
   

Для игрока А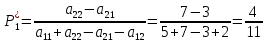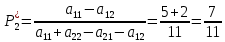





Для игрока В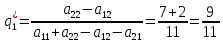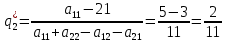





Таким образом оптимальное смешанные стратегии играков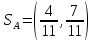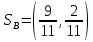

,

Цена игры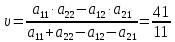



4.Графическим методом найти решение игры при заданной матрицей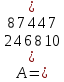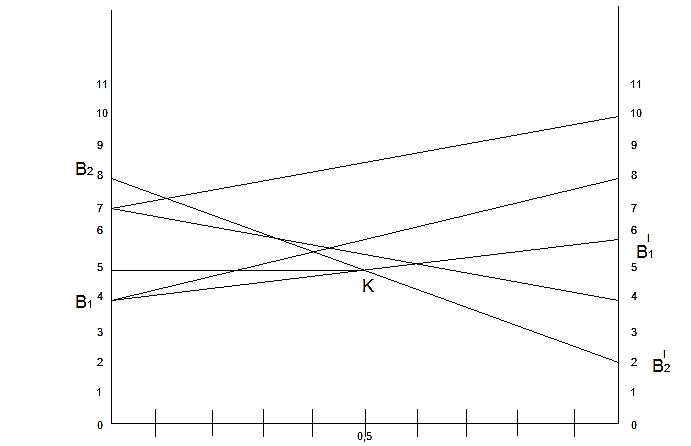





Нижняя граница выигрыша игрока В В₁ К В₂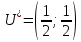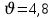





α₁ = 4, α₂ =2, α = 4

β₁ =8, β₂ = 7, β₃ =6_, β₄ = 8_, β₅ =10, β = 6

4 ≤ 𝜗 ≤ 6

5. Найти верхнюю и нижнюю цену игры заданной матрицей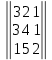



Определить седловые точки, если они существует, и найти минимаксные стратегии.

α₁ = min (3, -2, 1) = -2 α₂ = min (3, 4, -1) = -1

α₃ = min (1, -5, 2) = -5 α = max (α₁, α₂ , α₃) = -1

β₁ = max (3, 3, 1) = 3 β ₂ = max (-2, 4, -5) = 4

β₃ = max (1, -1, 2) = 2 β = min (β₁, β₂ , β₃) = β₃ = 2

α ≠ β Седловой точки нет

Минимаксные стратегии игроков

А₂ = (3, 4, -1), В₃ = (1, -1, 2)

Список литературы:

1. 
   https://function-x.ru/games_matrix_games.html
   
2. 
   https://math.semestr.ru/optim/nonlinear-programming.php
   
3. 
   http://www.consultant.ru/document/cons_doc_LAW_98330/2f9abd4ea0e7e8c44604f34458ae6335b10989cb/
   
4. 
   https://neftegaz.ru/tech-library/economy/146641-pribyl/