Российской федерации
 Скачать 110.5 Kb.
|
|
МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИМОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ) _____________________________________________________________ Кафедра «Физика-2»Утверждено редакционно-издательским советом университета , МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторным работам по дисциплине «Физика» Работы 7 Под редакцией В.А. КОЗЛОВА Москва - 2005 РАБОТА №7 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ Цель работы: экспериментальное определение коэффициента вязкости (коэффициента внутреннего трения) жидкости по методу Стокса. Приборы и принадлежности: стеклянный цилиндрический сосуд с вязкой жидкостью (с глицерином, касторовым или вазелиновым маслом); мелкие шарики из твердого материала (свинца, стали, стекла); микрометр; секундомер; масштабная линейка. Введение Вязкость (внутреннее трение) - свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Она оказывает существенное влияние на протекание многих процессов и ее необходимо учитывать при решении практических задач в различных областях науки и техники: гидро-, аэродинамике, гидравлике, механике трущихся поверхностей (рельс - колесо) и т. д. В 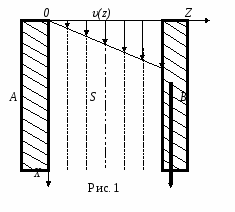 равновесном состоянии все слои жидкости (газа) покоятся друг относительно друга. При их относительном движении возникают факторы, стремящиеся уменьшить относительную скорость, то есть возникают силы торможения или проявляется вязкость. Механизм этих сил сводится к обмену импульсом упорядоченного движения между различными слоями, то есть, к переносу импульса упорядоченного движения. Поэтому возникновение сил трения в газах и жидкостях обусловлено процессом переноса, а именно процессом переноса импульса упорядоченного движения молекул.В  озникновение сопротивления, обусловленное вязкостью, поясним на следующем примере. Представим себе две пластины А и В (рис. 1), пространство между которыми заполнено жидкостью. Пластина В под действием тангенциальной (касательной) силы F движется с постоянной скоростью, пластина А - неподвижна. Слой жидкости, ближайший к пластине В, как бы «прилипает» к ней и движется с той же скоростью, а слой, непосредственно прилегающий к пластине А, - неподвижен. Мысленно разобьем жидкость на плоско-параллельные слои, перемещающиеся с различными скоростями. На рис.1 показана зависимость скорости слоя (z) от расстояния z до пластины А. Рассечем мысленно жидкость, заключенную между пластинами А и В, на две части площадкой S, параллельной скорости течения жидкости. Молекулы, находящиеся справа от S, обладают большей скоростью, а следовательно и большим импульсом, чем слева. Переходя из пространства BS в AS, молекулы передают часть своего упорядоченного импульса молекулам, с которыми они сталкиваются в левой части (AS). Аналогично, более медленные молекулы, попадая из левой части (АS) в правую, при столкновении отнимают часть упорядоченного импульса у молекул, расположенных в правой части (BS). В итоге жидкость в правой части испытывает как бы тормозящую силу, направленную против скорости . Таким образом можно объяснить возникновение сил внутреннего трения.Для пояснения этого факта некоторые авторы проводят следующую аналогию. Две железнодорожные платформы движутся по параллельным рельсам с различными скоростями. Грузчики, находящиеся на платформах, перебрасывают мешки с песком со своей платформы на соседнюю. Ясно, что в результате этого быстрее движущаяся платформа будет тормозиться, а медленнее движущаяся - ускоряться. Основной закон вязкого трения был установлен И. Ньютоном:  , (1)где F - тангенциальная сила, вызывающая сдвиг слоев жидкости друг относительно друга, S - площадь слоя, по которому происходит сдвиг,  - градиент скорости течения (быстрота её изменения от слоя к слою), - коэффициент вязкости (внутреннего трения) жидкости. Согласно формуле (1), - коэффициент вязкости жидкости численно равен тангенциальной силе, приходящейся на единицу площади, необходимой для поддержания разности скоростей равной единице, между двумя параллельными слоями жидкости, расстояние между которыми равно единице. В СИ измеряется в Пас (в СГС - пуаз). В условиях установившегося ламинарного течения при неизменной температуре T коэффициент вязкости - постоянная величина, независящая от градиента скорости. Коэффициент вязкости имеет различные значения для разных жидкостей. Так, например, глицерина (при температуре t = +20C) в 1,5 тыс. раз больше, чем у воды. Для данной жидкости коэффициент зависит от параметров, характеризующих ее внутреннее состояние, и в первую очередь от температуры, понижаясь с ростом Т. Так, вязкость воды при изменении температуры от 0C до +100C уменьшается от 1,8103 до 2,8104 Пас. Особенно сильно зависит от температуры вязкость масел; так, например, вязкость касторового масла при повышении температуры от +18С до +40С падает почти в четыре раза. Коэффициент внутреннего трения жидкости может быть найден путем измерения силы трения, возникающей при падении твердого тела (например, шарика) в этой жидкости. Различие скоростей слоев жидкости возникает потому, что в результате взаимного притяжения между частицами жидкости и падающего шарика ближайший к нему слой движется с его же скоростью, а остальные - со все уменьшающейся . Слой жидкости, примыкающий к стенкам сосуда, имеет скорость, равную нулю. Величину силы трения можно определить следующим образом. На твердый шарик, падающий в жидкости, действует три силы:
P  r31g,(2)где r - радиус шарика; 1- плотность материала шарика при данной температуре; g - ускорение свободного падения.
FA r32g,(3)(здесь 2 - плотность жидкости при данной температуре).
Fтр 6,(4) где - скорость движения шарика; - искомый коэффициент внутреннего трения. В 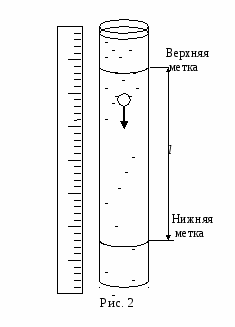 результате действия на шарик трех сил он будет двигаться под действием их равнодействующей F. Согласно формулам (2), (3) и (4),F P FА Fтр. Силы P и FА постоянны, а Fтр растет с увеличением скорости шарика. Это приводит к тому, что равнодействующая данных сил будет уменьшаться до тех пор, пока не станет равной нулю: F P FА Fтр 0.(5) Начиная с этого момента, шарик будет двигаться равномерно. Подставляя значения действующих сил, а также формулы (2), (3) и (4) в выражение (5), получим условие равномерности движения шарика в виде r3g(2 1) 6 0,откуда может быть определено значение . Подставляя в это уравнение скорость установившегося равномерного движения lt (здесь l - путь, который проходит шарик за время t) и учитывая, что диаметр шарика d 2r, получаем окончательное выражение для расчета коэффициента внутреннего трения жидкости:  (6)Порядок выполнения работы Прибор, как было сказано выше, представляет собой вертикальный стеклянный цилиндр, наполненный исследуемой жидкостью. На цилиндре снаружи имеются две метки (кольца) в верхней и нижней частях. Эти метки определяют некоторый участок пути равномерно движущегося шарика (рис. 2). Верхняя метка должна быть ниже уровня жидкости на 20-25 см, чтобы шарик, подходя к метке, уже двигался равномерно. Шарики надо опускать ближе к оси цилиндра. Перед опусканием шариков в жидкость следует определить их размеры. Ввиду того, что шарики далеко не идеальной формы, с целью уменьшения ошибки измерения диаметр каждого из них измеряется микрометром не менее пяти раз в различных направлениях. Все результаты измерений записываются в таблицу. Затем каждый шарик бросают в жидкость и измеряют время t, за которое он проходит путь l между метками в сосуде. Для измерения времени служит секундомер, который включается в момент прохождения шариком верхней метки и выключается в момент прохождения шариком нижней метки. Длина пути, то есть расстояние между метками измеряется при помощи масштабной линейки. Опыт необходимо провести не менее чем с пятью разными шариками и вычислить среднее арифметическое значение коэффициента внутреннего трения жидкости ср. Значения плотностей материалов шариков и жидкости берутся из справочных таблиц. Результаты всех измерений и вычислений заносятся в таблицу с указанием системы единиц и размерностей. Таблица
Обработка результатов измерений I. Используяэкспериментальные данные, вычислите величины погрешностей в Вашем опыте и сравните их с погрешностями, которые рассчитываются теоретически для данной методики измерений. Рассчитайте по экспериментальным данным среднее значение коэффициента внутреннего трения жидкости:  .Случайная ошибка dизмерения диаметра d шарика рассчитывается по формуле 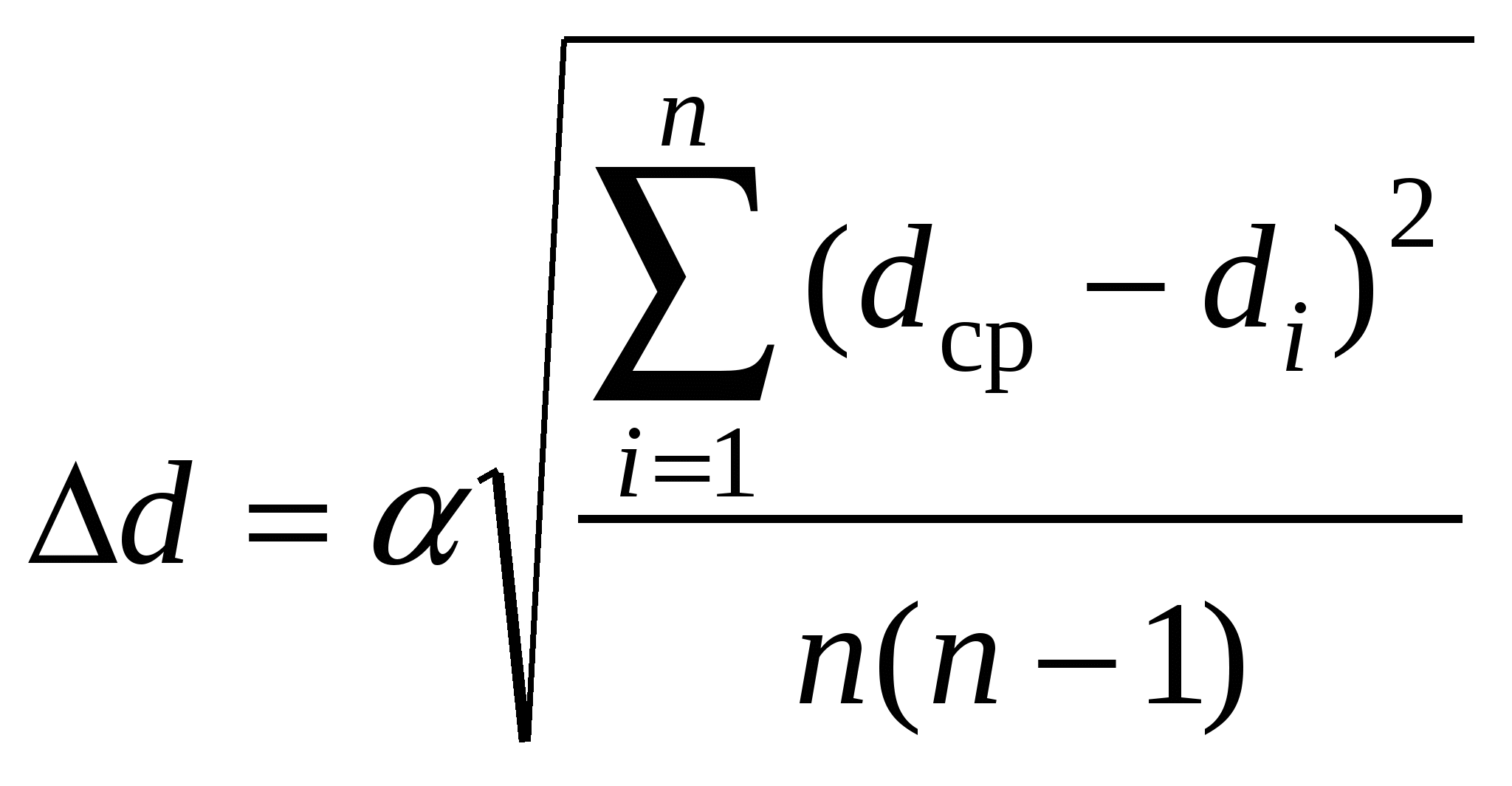 , (7)где n - число измерений. Для доверительной вероятности 0,9 и числа измерений n = 5 коэффициент Стьюдента = 2,8 (см., например, методические указания [5, 6]). Рассчитайте среднюю абсолютную ошибку измерения коэффициента внутреннего трения, после чего вычислите среднюю относительную погрешность измерений коэффициента внутреннего трения  (8)и выразите её в процентах. Измеренный коэффициент внутреннего трения жидкости представьте в следующем виде: ср. (9) II. Расчеттеоретический погрешностей измерений. Согласно теории погрешностей для избранной методики измерений, применяя формулу (6), получаем следующее выражение относительной ошибки определяемой величины  , (10)где d, t и l - абсолютные ошибки, допускаемые при измерении соответствующих величин и равные половине цены деления прибора, используемого при измерении данной величины. Абсолютная ошибка измерения табличных величин g, 1 и 2 принимается равной пяти единицам следующего знака, а абсолютная ошибка выражения (1 - 2) равна сумме ошибок измерений 1 и 2. По относительной ошибке измерений вычислить абсолютную ошибку измерений коэффициента внутреннего трения жидкости . Результат записать в виде ср. (Измерение может быть произведено с ошибкой . . . . . %). Сравните величину фактической ошибки ср результатов эксперимента с ошибкой, допускаемой при данной методике измерений. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. При каких условиях сила внутреннего трения жидкости пропорциональна скорости? 2. Объясните зависимость величины коэффициента внутреннего трения от температуры. 3. Напишите размерность коэффициента внутреннего трения (коэффициента вязкости). 4. Можно ли изменять длину пути, пройденного шариком, передвижением верхней метки на сосуде? 5. Можно ли измерять длину пути, пройденного шариком, передвижением нижней метки на сосуде? 6. Как изменяются скорость и ускорение при прохождении шариком пути между поверхностью жидкости и верхней меткой? 7. Как изменяется скорость падения парашютиста при затяжном прыжке? СПИСОК ЛИТЕРАТУРЫ
| ||||||||||||||||||||||||||||||||||||||||||||||