Курсова. Курсач. Розрахунок та оптимізація характеристик системи електрозвязку
 Скачать 260.75 Kb. Скачать 260.75 Kb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДЕРЖАВНИЙ УНІВЕРСИТЕТ ТЕЛЕКОМУНІКАЦІЙ Кафедра телекомунікаційних систем та мереж Курсова робота З дисципліни «Теорія передачі сигналів в інфокумунікаційних мережах» на тему: «Розрахунок та оптимізація характеристик системи електрозв’язку» Варіант №4 Студента 2 курсу Групи ТСД-25 Григор’єва Владислава Тимуровича Викладач: доц. Варфоломеєва О.Г. Київ – 2019 Зміст Вхідні дані до курсової роботи Вступ Структурна схема цифрової системи передачі (ЦСП). Розрахунок характеристик аналого-цифрового перетворення та інформаційних характеристик повідомлень на виході АЦП. Розрахунок характеристик завадостійкості прийому сигналу в дискретному каналі. Вибір корегуючого коду і розрахунок характеристик завадостійкого декодування. Розрахунок пропускної спроможності каналу зв’язку. Розробка структурної схеми демодулятора. Розрахунок ефективності системи передачі. Висновок. Варіант
1. Структурна схема цифрової системи передач (ЦСП). Зобразити структурну схему ЦСП неперервних повідомлень, яка містить джерело та Одержувач повідомлень, АЦП і ЦАП, кодер і декодер завадостійкого коду, модулятор і демодулятор, лінію зв’язку та джерело завад. Зобразити часові діаграми в усіх точках схеми, задавши вільну форму неперервного вихідного сигналу та числом рівнів квантування. Пояснити, з яких міркувань вибираються інтервал дискретизації за часом і крок квантування за рівнем. До часових діаграм дати необхідні пояснення, виходячи з призначення кожного блоку. Рішення: Структурна схема цифрової системи передачі (ЦСП) має наступний вигляд:   Дж.пов. АЦП       Код.дж. Кв. Дискр.          Пр.пов ФНЧ Декод. Демод. Л Мод. Код.к. Дж.Пер.         ЦАП Елементи структурної схеми цифрової системи передачі (ЦСП) неперервних повідомлень: Дж. Пов. (джерело повідомлення) Дискр. (дискретизатор) Кв. (квантувач) Код. Дж. (кодер джерела) Код. к. (кодер каналу) Мод. (модулятор) Л (лінія зв’язку) Дж. Пер. (джерело перешкод) Демод. (демодулятор) Декод. (декодер) ФНЧ (фільтр нижніх частот) Отже, часові діаграми для структурної схеми ЦСП безперервних повідомлень в зазначених точках мають наступний вигляд:                  B(t) 10 B(t) B(t) 10 B(t)8 6 Вихід джерела повідомлення 4 2 t 0 t B(t) B(t)       Вихід квантувача Вихід джерела Вихід квантувача Вихід джерела t t t Ч.М. 2. Розрахунок характеристик аналого-цифрового перетворення та інформаційних характеристик повідомлень на виході АЦП. 2.1. По заданій верхній граничній частоті спектру повідомлення, пік фактору сигналу П та допустимому відношенні сигнал/завада квантування Рк визначити: 1) мінімально допустиме число рівнів квантування L (L вибирають рівним цілого степеня числа 2); 2) значність кодових комбінацій та тривалість символу на виході АЦП, вважаючи, що тривалість кодової комбінації дорівнює інтервалу дискретизації. 2.2 Знайти ентропію незалежних дискретних повідомлень на виході АЦП та продуктивність джерела повідомлень, якщо імовірність передачі символу: Р(1)=0,02 Рішення: 2.1. 1) Розрахуємо число рівнів квантування, скориставшись формулою: p = 3(L-1)2 П2   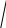  L = p*П2 +1 3 p(дБ) = 10*lg p p(рази) = 100,1*p(дБ)  p(раз) = 10 p(дБ) 10  p(раз) = 10 p(дБ) = 794(раз) 10 Пік фактор сигналу: П=3  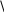 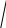  L =П pхв(раз) +1 L =П pхв(раз) +1 3  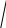   L = 3 794 +1 = 3*16+1 = 49 L = 3 794 +1 = 3*16+1 = 49 3 Так як число рівнів квантування має відповідати умові L = 2n, то обираємо 26 = 64.   L = 49 64 L = 49 642) За умовою тривалість кодових комбінацій рівна інтервалу дискретизації, отже значність кодових комбінацій та тривалість сигнала на виході АЦП будуть обраховані наступним чином: k = log2 (L) = log2 64 = 6 Тривалість першого символу кодової комбінації: То = 1 fд * k fд = (2,3/2,5)FB FB = 4*103 Гц fд = 2,5*4*103 = 10*103 Гц To = 1 = 1,66*10-5(c) 10*103*6 2.2 Ентропія   2 2  Н(А) = - p(ai)*log2 p(ai) (біт/симв) i=1 Номер варіанту чотири, отже: P(1) = 0,04 – імовірність появи одиниці. Тоді імовірність появи нуля дорівнює: P(0) = 1 – P(1)= 1 – 0,04 = 0,96 Виходячи із отриманих імовірностей, визначимо ентропію: H(A) = -(0,04*log2(0,04)+0,96*log2(0,96)) = 0,07 (біт/симв) Згідно з отриманим значенням ентропії розрахуємо продуктивність джерела: H(A) = 0,13 = 7*103 ( біт ) H`(A) = To 1,66*10-5 с 3. Розрахунок характеристик завадостійкості прийому сигналів у дискретному каналі. 3.1. Вважаючи канал зв’язку каналом із постійними параметрами, побудувати залежність імовірності помилки двійкового символу на виході оптимального демодулятора від відношення енергії сигналу Е до спектральної щільності потужності завади No на виході демодулятора, h2=E/No, для чого розрахувати 5..7 значень Pзав, задавши такі значення, при яких Рош зміниться від 0,5 до 10-6: зав = f(h) Формула для розрахунку імовірності помилки обрана з урахуванням методу модуляції та способу прийому. Розрахувати імовірність помилки символу на виході демодулятора для заданих виду та способу прийому, вважаючи, що в каналі зв’язку немає завадостійкого кодування. Амплітуда модульованого сигналу а (потужність сигналу Pc=a2/2) та спектральна щільність потужності завади No на вході демодулятора задані. Зробіть висновок про необхідність застосування завадостійкого коду. Рішення: розрахуємо миттєву потужність сигналу: (0,2)2 = 0,02 (B2), Pc = a2/2 = 2 Енергія сигналу: E = Pc*To = 0,02*1,66*10-5 = 0,03*10-5 (в2/Гц)    Коефіцієнт, що характеризує відношення сигнал/шум: Коефіцієнт, що характеризує відношення сигнал/шум: E = 0,05*10-5 = 0,02*103 = 4,5 E = 0,05*10-5 = 0,02*103 = 4,5   h= No 2,5*10-8 K=1 h= No 2,5*10-8 K=1Імовірність помилки на виході демодулятора визначається формулою: Рпом = 0,5[1-Ф(kh)] = 0,5 [1-Ф(kh)]=3,5*10-6 Значення Ф(kh) будем обрати за таблиці Крампа Задамо наступні значення Pпом: Pпом = {0,5;0,1; 10-2;10-3; 10-4; 10-5; 10-6} Формула для розрахунку Ф(h) у загальному вигляді буде: Ф(h) = 0,5 - Рпом 0,5 Рпом = 0,5; Ф(h) = 0; h = 0. Рпом = 0,1; Ф(h) = 0,8; h = 1,28 Pпом = 10-2 = 0,01; Ф(h) = 0,98; h = 2,35 Pпом = 10-3 = 0,001; Ф(h) = 0,998; h = 3,1 Pпом = 10-4 = 0,0001; Ф(h) = 0,9998; h = 3,7 Pпом = 10-5 = 0,00001; Ф(h) = 0,99998; h = 4,3 Pпом = 10-6 = 0,000001; Ф(h) = 0,999998; h = 4,8 За отриманими даними побудуємо графік залежності Рпом = f(h);    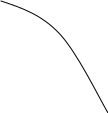 1 2 3 4 5 h 1 2 3 4 5 h0,5 0,1 10-2 10-3 10-4 10-5 10-6 Pпом 4. Вибір корегуючого коду та розрахунок характеристик завадостійкого декодування. 4.1. Сигнал з виходу АЦП надходить на вхід кодера завадостійкого коду. В каналі зв’язку використовується завадостійке кодування систематичним кодом (10.6) або (11.7) з мінімальною кодовою відстанню d0 = 3. Для трьох рівнів квантування, заданих у таблиці, записати кодові комбінації на виході завадостійкого кодера. Виробляючі матриці кодів:     1000001100 10000001100 1000001100 10000001100 0100000110 01000000110 G(10.6) = 0010000011 . G(11.7) = 00100000011 0001001010 00010001010 0000100101 00001000101 0000011001 00000011110 Визначити відстані між комбінаціями на вході кодера та між комбінаціями на його виході. Визначте тривалість символу на виході кодера завадостійкого коду. Зробіть висновок про корегуючі можливості коду. 4.2. Розрахуйте імовірності однократних та двократних помилок на вході декодера. Зробіть висновок про те, чи поліпшиться завадостійкість прийому при виправленні декодером однократних помилок. Описати принцип виправлення однократної помилки для випадку передачі комбінації. Рішення: 4.1. Для початку закодуємо задані рівні квантування двійковим кодом: 14(10) = 011000(2) 44(10) = 101100 (2) 51(10) = 110011 (2) Твірна матриця для нашого випадку Р(10,6) має вигляд: 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 1 0 Р(10,6) = 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 1 1 0 0 1 Транспонуємо твірну матрицю для отримання перевірочної. Транспонована матриця має вигляд: 1 0 0 1 0 1 Р’(10,6) = 1 1 0 0 1 0 0 1 1 1 0 0 0 0 1 0 1 1 Розрахуємо перевірочні розряди для заданих рівнів квантування: Для 14 r1 = 0 * 1О1 * 0О0 * 0О1 * 1О0 * 0О1 * 1 = 0 r2 = 0 * 1О1 * 1О0 * 0О1 * 1О0 * 0О1 * 1 = 1 r3 = 0 * 1О0 * 0О0 * 0О0 * 1О1 * 0О1 * 1 = 1 r4 = 0 * 1О1 * 0О0 * 1О0 * 1О0 * 0О1 * 1 = 0 Для 44 r1 = 0 * 1О1 * 0О1 * 1О1 * 1О0 * 0О1 * 1 = 1 r2 = 0 * 0О1 * 1О0 * 1О1 * 1О0 * 0О1 * 1 = 1 r3 = 0 * 1О1 * 0О0 * 0О1 * 1О1 * 0О0 * 1 = 1 r4 = 0 * 1О0 * 1О0 * 0О0 * 1О0 * 0О1 * 1 = 0 Для 51 r1 = 0 * 1О1 * 1О0 * 0О1 * 1О0 * 0О1 * 1 = 1 r2 = 0 * 1О1 * 0О0 * 0О1 * 0О0 * 0О1 * 1 = 0 r3 = 0 * 1О0 * 0О1 * 1О0 * 1О1 * 0О1 * 1 = 1 r4 = 0 * 1О1 * 0О0 * 0О0 * 1О1 * 1О1 * 1 = 0 Для рівня 14: 0110000110 Для рівня 44: 1011001110 Для рівня 51: 1100111010 Визначимо кодову відстань у кодовій комбінації на вході АЦП.
Визначимо кодову відстань у кодовій комбінації на виході АЦП.
Тривалість символу на виході кодера завадостійкого коду обрахуємо за формулою: 1 1 tk = fa * n = 10 * 103 * 10 = 1 * 10-5 c 4.2. Імовірність помилок на вході декодера визначається за формулою: Pg = Cng * Pошg * (1-Pош)n-g Де: g – кратність помилки, n – кількість розрядів кодової комбінації; Для знаходження кількості комбінацій Cng, скористаєвмося формулою : n! Cgn = g!*(n-g)! Кількість розрядів кодової комбінації n = 10, звідси: Для однократної помилки 10! 10! C110 = 1!*(10-1)! = 1!*9! = 10 Для двократної помилки 10! 10! 9*10 C210 = 2!*(10-2)! = 2!*8! = 2 = 45 Звідси імовірність однократних помилок (g = 1); P1=C110*Pпом1*(1-Рпом)10-1=10*3,5*10-6*(1–3,5*10-6)9=3,5*10-5*(0,999)9= =3,5*10-5*0,99=1,675*10-5 Імовірність двократних помилок (g = 2); P2=C210*Pпом2*(1-Рпом)10-2=45*(3,5*10-6)2*(1–3,5*10-6)8 =45*(3,5*10-12)*(0,99)8= =101,25*10-12*0,99=1*10-10 5. Розрахунок пропускної спроможності каналу зв'язку. 5.1. Визначити пропускну спроможність дискретного каналу: вхід модулятора – вихід демодулятора Сg. Значення імовірності помилки символу розраховано раніше в пункті 3. Порівняти пропускну спроможність дискретного каналу з продуктивністю джерела цифрового повідомлення, зробити висновки на підставі теореми Шеннона. 5.2. Визначити пропускну спроможність неперервного каналу, необхідну для передачі цифрових сигналів, при цьому потужність сигналу розраховувалась в п. 3., спектральна потужність завади No береться з вхідних даних, а смуга попускання Fk розраховується , виходячи з спектру сигналу. 2 5 FkAM = F k()()ф = to ; Fkчч = to ; to – тривалість символу на вході модулятора. Рішення: 5.1. Визначимо пропускну здатність дискретного каналу Сд = v[1+Pпом*log2Pпом + (1-Рпом)*log2(1-log2Pпом)], 1 v= tk Підставимо свої дані, та отримаємо: 1 Сд = 1,66*10-5[1+(3,5*10-6log23,5*10-6)+(1-3,5*10-6)*log2(1-3,5*10-6)]=60240,96[1+(0,99+ (-2,5*10-6)+(-18,61)]=59642(біт/с) Так як Н’(А)<Са (7000(біт/с)<59642(біт/с)), то згідно з теоремою Шеннона існує такий спосіб кодування і декодування, при якому імовірність помилкового декодування і ненадійність можуть бути як завгодно малі. 5.2. Визначимо пропускну спроможність неперервного каналу (вихід модулятора і вхід демодулятора – лінію зв'язку):  CH= Flog2(1+Pc/Pn)  Pn = No* F = 5*105*2,5*10-8=12,5*10-3 Pn = No* F = 5*105*2,5*10-8=12,5*10-35  F = tk F = tk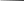 5 5 F = 1*10-6 = 5*105 F = 1*10-6 = 5*105Розрахуємо пропускну здатність неперервного каналу:   СН = F*log2(1+Pe/ F*No)= 5*105*log2(1+(0,03/12,5*10-3))=5*105*1,766=884000(біт/с) СН = F*log2(1+Pe/ F*No)= 5*105*log2(1+(0,03/12,5*10-3))=5*105*1,766=884000(біт/с)Порівняємо отримані значення пропускної здатності дискретного каналу та пропускної здатності неперервного каналу для передачі цирових сигналів: СН=884000>Сд=59642 Висновок: неперервний канал набагато краще підходить для передачі цифрових сигналів, ніж дискретний канал. 6. Позробка структурної схеми демодулятора Представити структурну схему демодулятора для заданого виду модуляції та способу прийому, записати алгоритм прийому, описати призначення та принцип роботи його вузлів. Рішення: Будь-який приймач націлений на те, щоб збільшити відношення потужності сигналу до потужності помилки. Котельников вивів умову оптимального прийому, яка виглядає наступним чином: 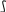 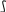 [x(t)-Si(t)]dt>< [x(t)-Si(t)]dt [x(t)-Si(t)]dt>< [x(t)-Si(t)]dtДе: Si, Sj – еталонні сигнали «0» та «1», які виробляє генератор. x(t) – сигнал, який поступає на прийом. Вибір схеми оптимального приймача залежить від виду модуляції: для ЧМ – схема виглядає наступним чином, адже енергія сигналів «0» та «1» однакова Е1=Е2.  Si(t) Si(t)  Г Г    Si(t)*X(t) Si(t)*X(t) Si Si(t)*X(t) Si(t)*X(t) Si      X X  X(t) X(t)  ВП ВП  Sj(t)*X(t) Sj(t)*X(t) S0j Sj(t)*X(t) Sj(t)*X(t) S0j        Х Х Г Sj(t)   x(t)Sj(t)dt>< x(t)Sj(t)dt x(t)Sj(t)dt>< x(t)Sj(t)dtФункціональні блоки мають наступне призначення:    - блок множення – здійснює множення двох поданих на нього сигналів;   - блок інтегрування – обраховує функцію взаємної кореляції прийнятого сигналу і - блок інтегрування – обраховує функцію взаємної кореляції прийнятого сигналу і варіанту переданого сигналу;  Г - генератор опорних сигналів;  ВП - вирішуючий пристрій – приймає рішення на користь того еталонного сигналу, у якого взаємна кореляційна функція з прийнятим сигналом найбільша. 7.Розрахунок ефективності системи передачі   Розрахувати коефіцієнти n, B, y, які визначають ефективність системи зв’язку, вважаючи, що втрати інформації в каналі зневажливо малі і швидкість передачі дорівнює продуктивності джерела повідомлень. Рішення: Коефіцієнт використання каналу по пропускній здатності: RH Н’(А) 7*103  n= Cд = Cд = 59642 = 0,11 (біт/с) Коефіцієнт використання каналу по полосі частот: H`(F) 7*103   В = Рс/Рп = Рс = 0,03 = 4375 (біт/с) No F 2,5*10-8*5*105 Коефіцієнт використання каналу по потужності:  RH 3*104  y= F = 5*105 = 0,06(біт/с) 8.Висновок У даній курсовій роботі розраховані основні параметри системи: характеристики АЦП і інформаційні характеристики на виході АЦП; характеристики завадостійкого прийому сигналу у дискретних каналах; характеристики завадостійкого декодування; пропускна спроможність дискретного і неперервного каналу зв’язку; коефіцієнти ефективності системи; Основною перевагою цифрової системи передачі у порівнянні з неперервними системами являється висока перешкодостійкість. Ця перевага проявляється у системах передачі сигналу і його багатократної ретрансляції. У кабельних і радіорелейних лініях великої протяжності викривлення у окремих ланках, як правило, накопичуються, так як адитивні завади є статично незалежними і їх потужність на виході буде дорівнювати сумі потужностей завад усіх ланок. Завадостійкість при цифровій системі передачі підвищує достовірність передаваної інформації. Високий ступінь завадостійкості дозволяє здійснювати практично необмежений за дальністю зв’язок, використовуючи канали порівняно невисокої якості. |
