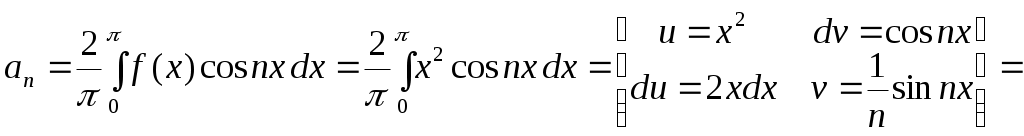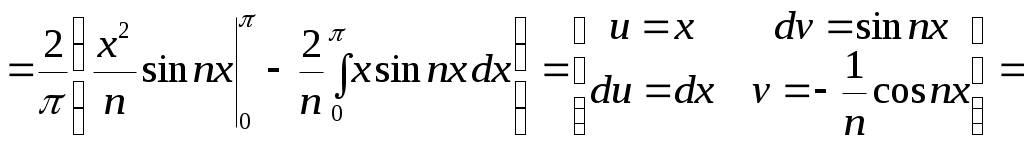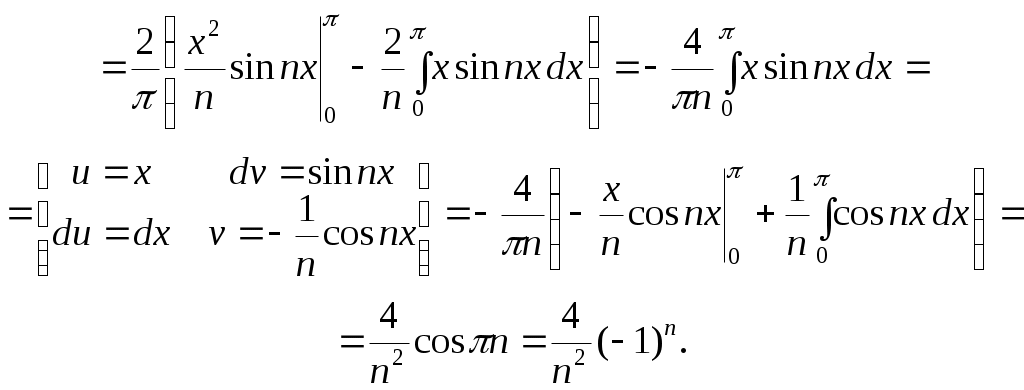|
Ряды Фурье_практика. Рядом Фурье функции. Ряд Фурье интегрируемой функции может сходиться, причем не обязательно к функции, либо расходиться. Условия сходимости ряда Фурье были установлены немецким математиком Дирихле. Теорема 1
Ряды Фурье.
Пусть 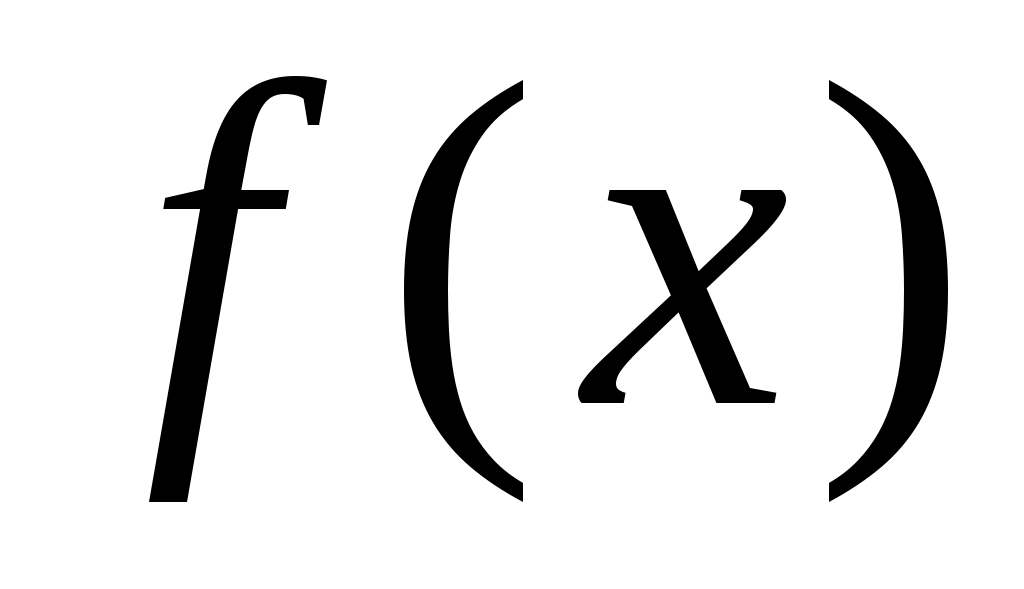 интегрируемая периодическая с периодом интегрируемая периодическая с периодом 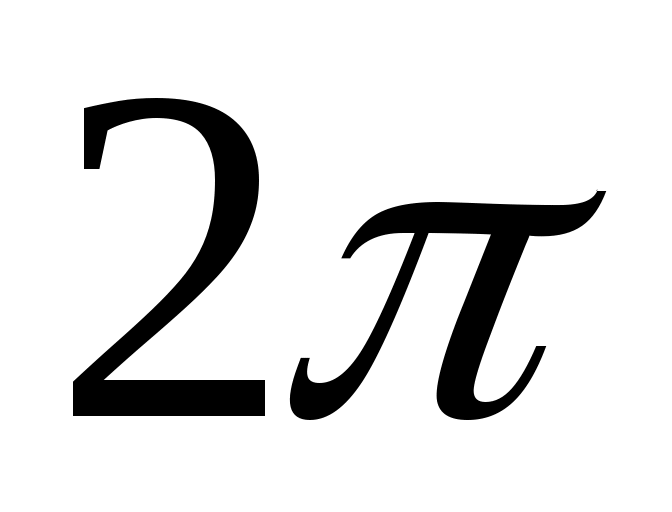 функция. Функциональный ряд вида функция. Функциональный ряд вида
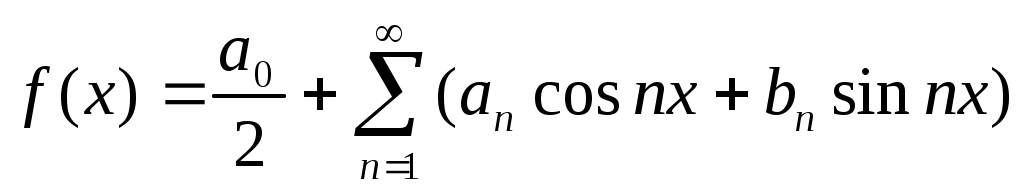 , (1) , (1)
где коэффициенты 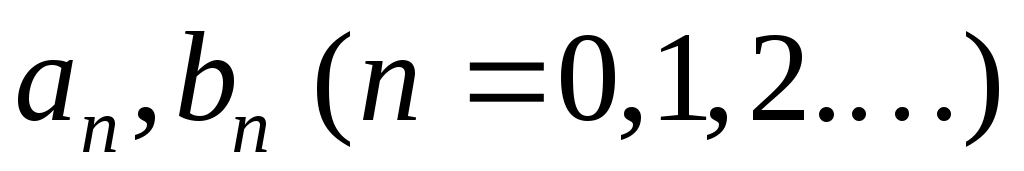 определяются по формулам: определяются по формулам:
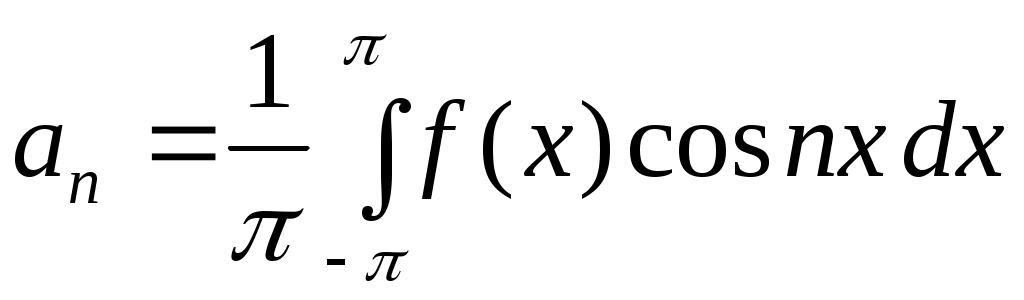 , (2) , (2)
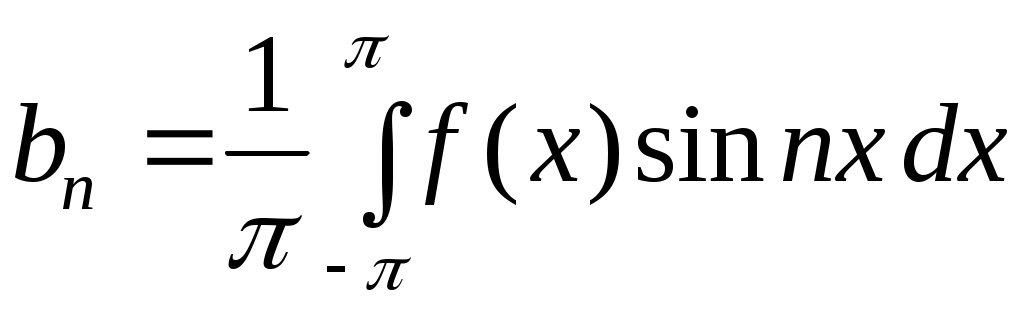 , (3) , (3)
называется рядом Фурье функции 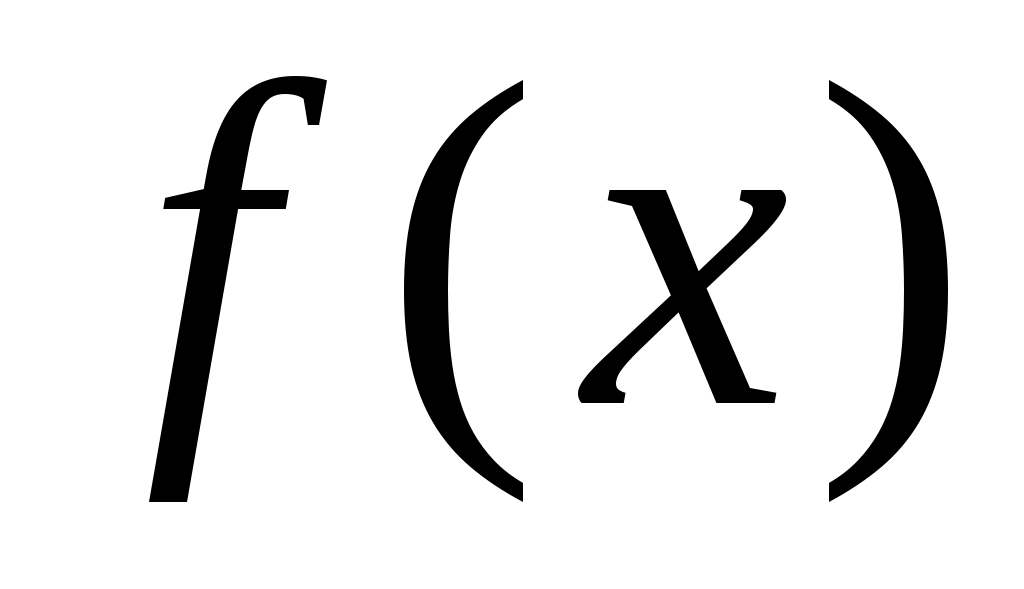 . .
Ряд Фурье интегрируемой функции 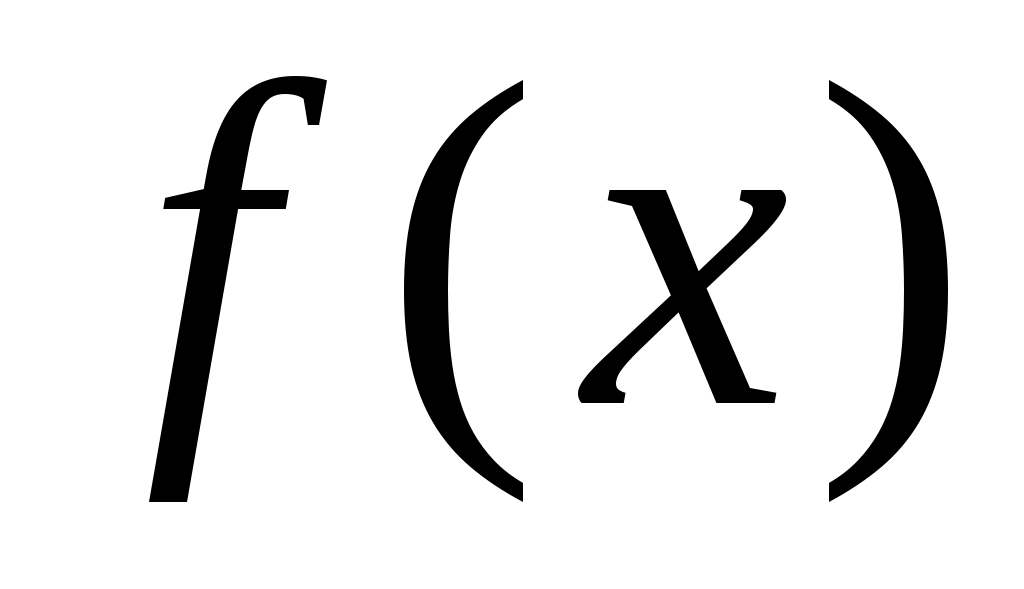 может сходиться, причем не обязательно к функции может сходиться, причем не обязательно к функции 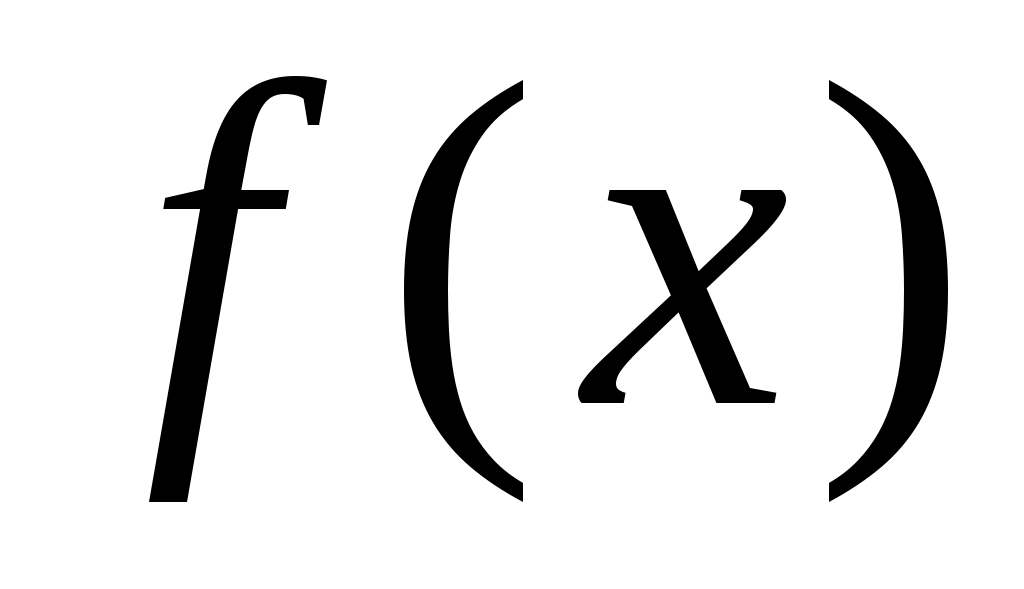 , либо расходиться. Условия сходимости ряда Фурье были установлены немецким математиком Дирихле. , либо расходиться. Условия сходимости ряда Фурье были установлены немецким математиком Дирихле.
Теорема 1. (Дирихле). Если функция 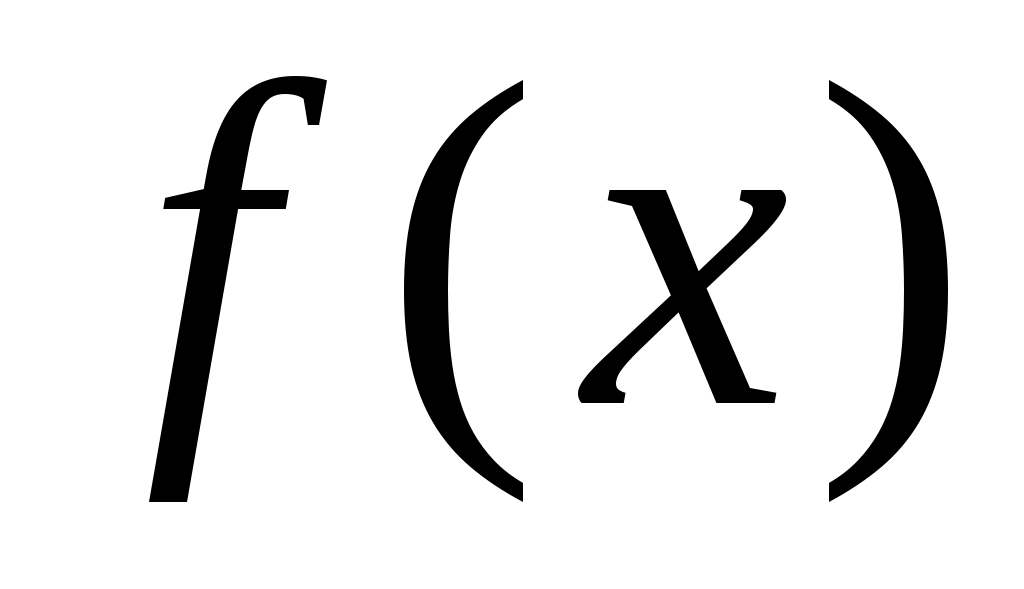 на отрезке на отрезке 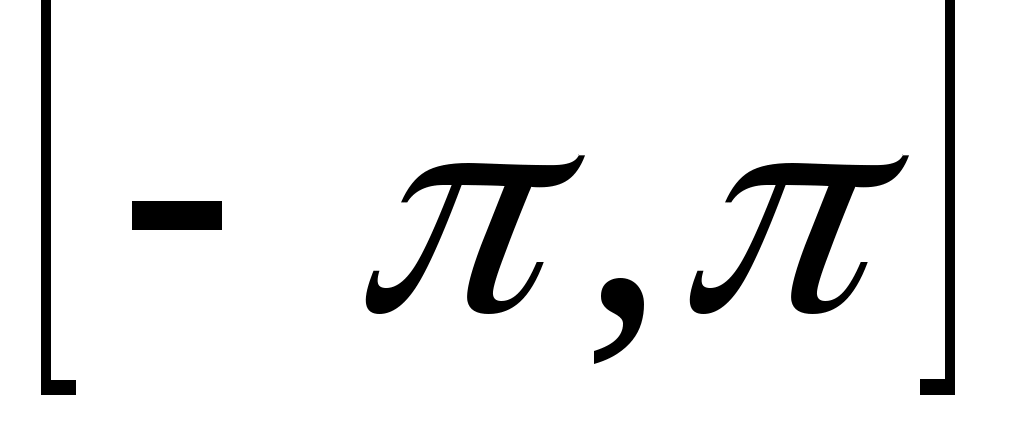 непрерывна или имеет конечное число точек разрыва первого рода и при этом монотонна или имеет конечное число экстремумов на непрерывна или имеет конечное число точек разрыва первого рода и при этом монотонна или имеет конечное число экстремумов на 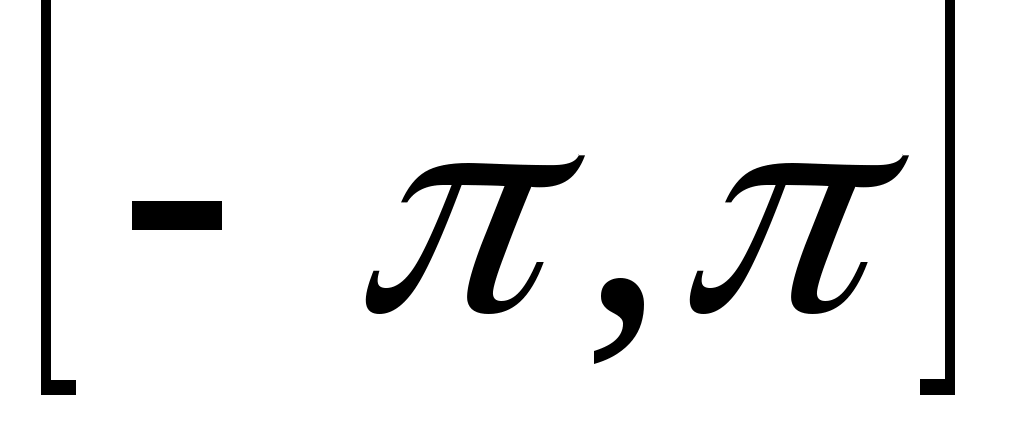 , то ряд Фурье для любых , то ряд Фурье для любых 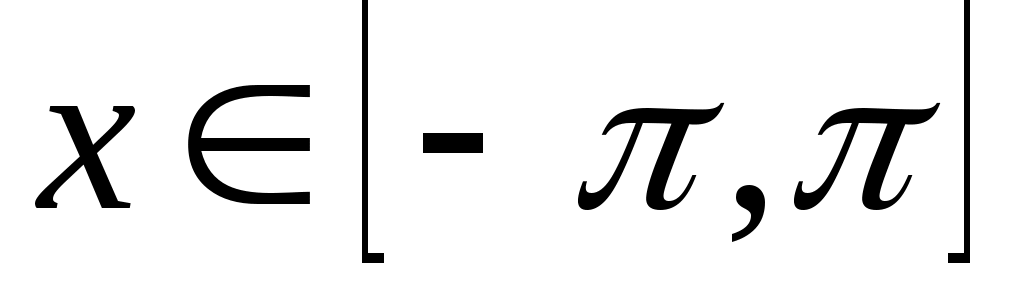 сходится к функции сходится к функции 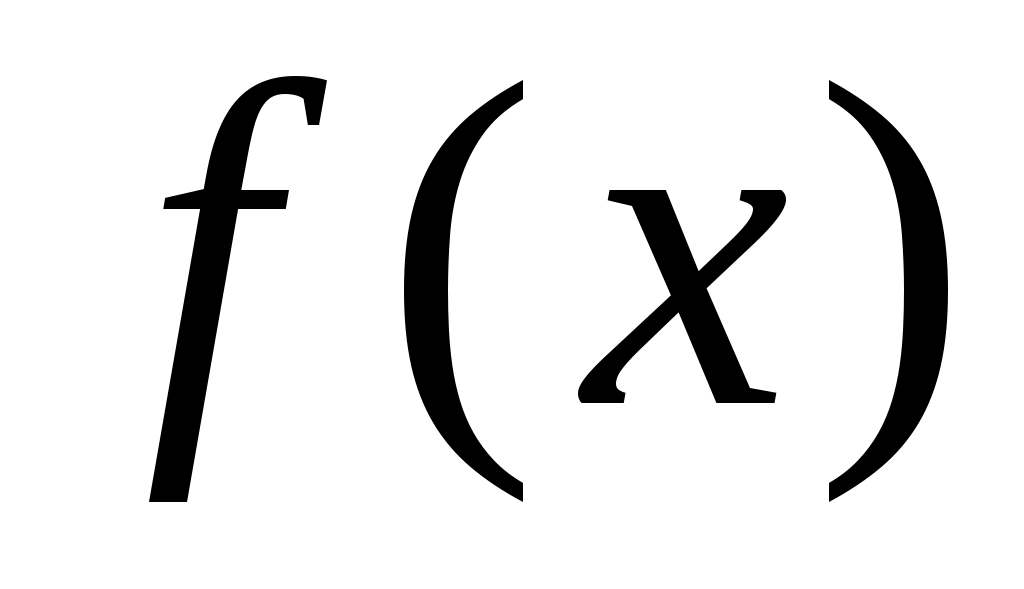 . .
Пусть функция 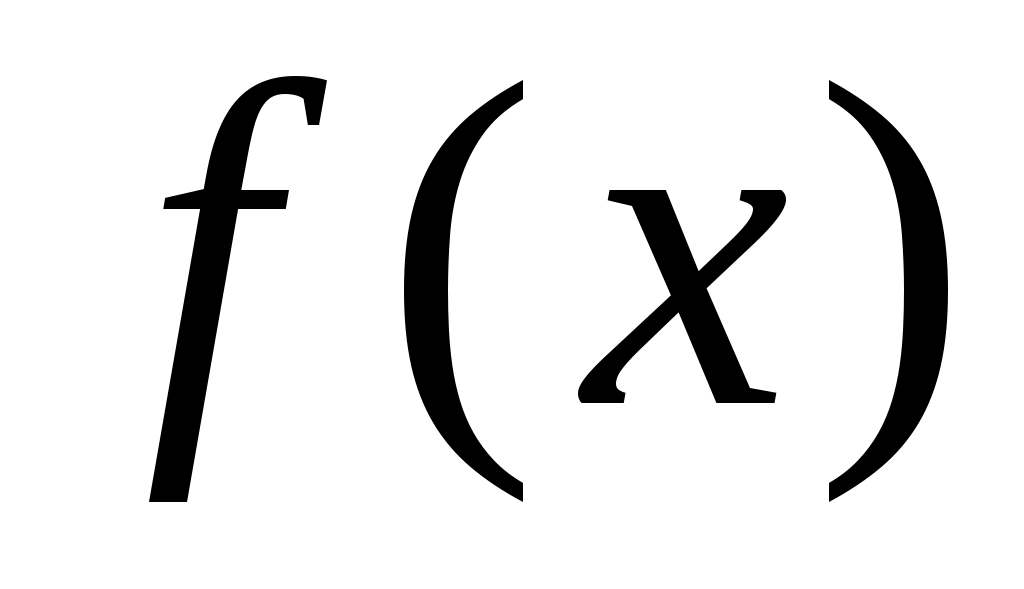 четная для всех четная для всех 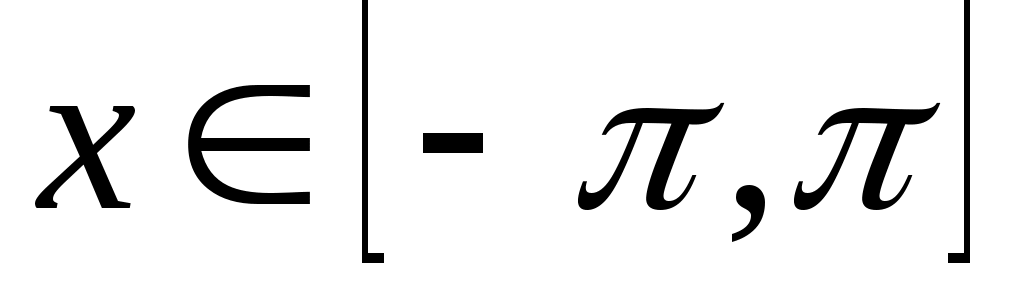 . Тогда . Тогда 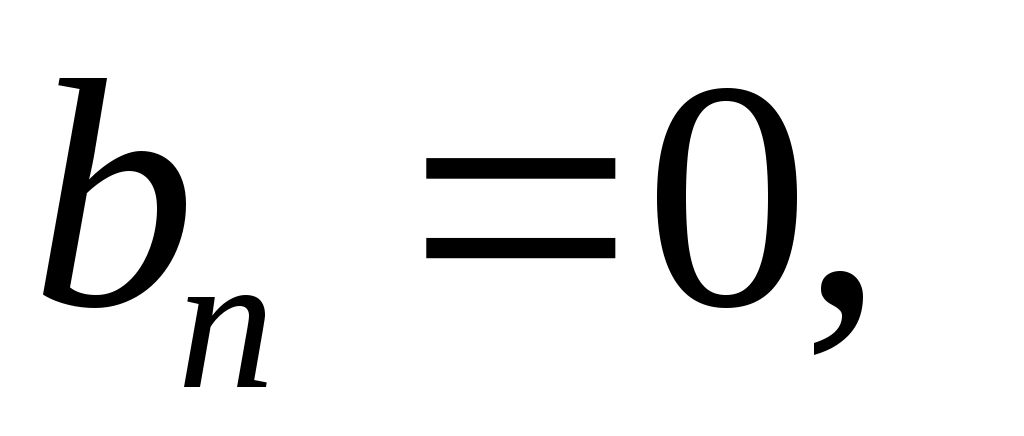 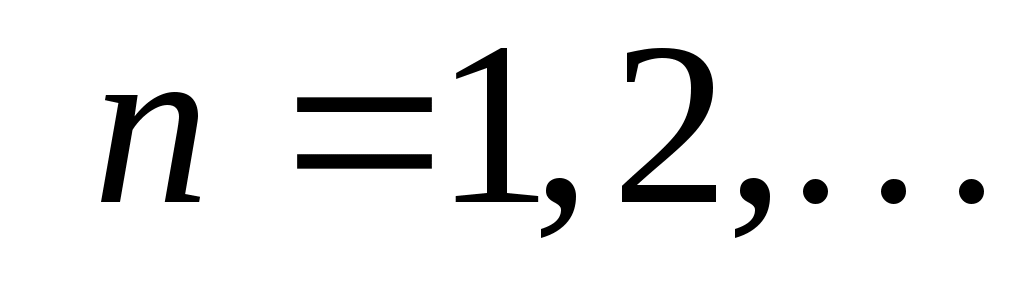 и ряд Фурье имеет вид: и ряд Фурье имеет вид:
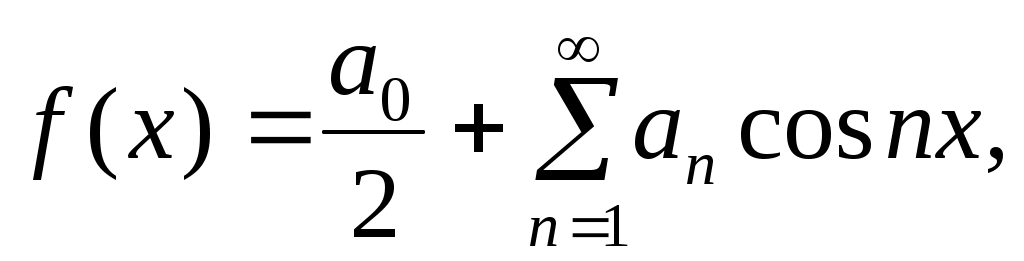
где 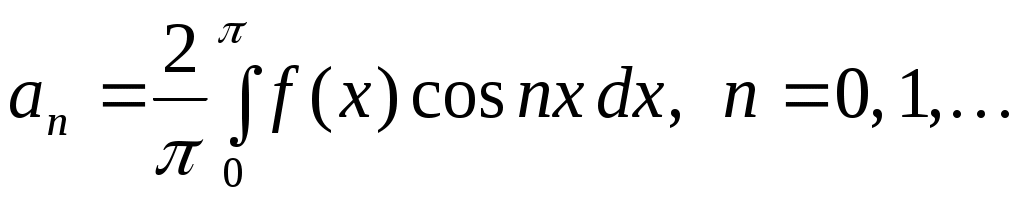 . (4) . (4)
Следовательно, четная функция разлагается в ряд Фурье по косинусам. Аналогично нечетная функция 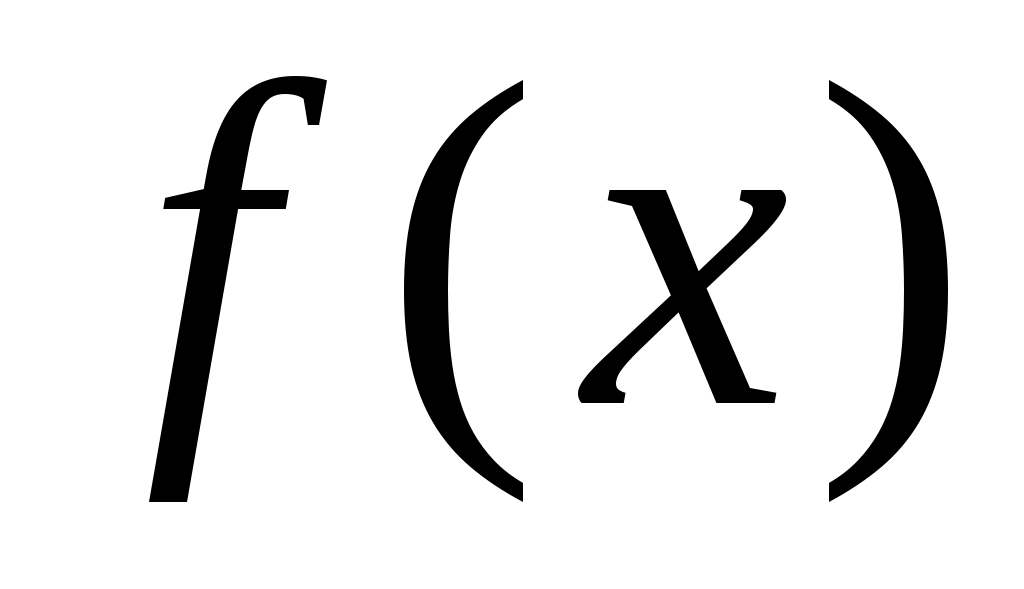 для всех для всех 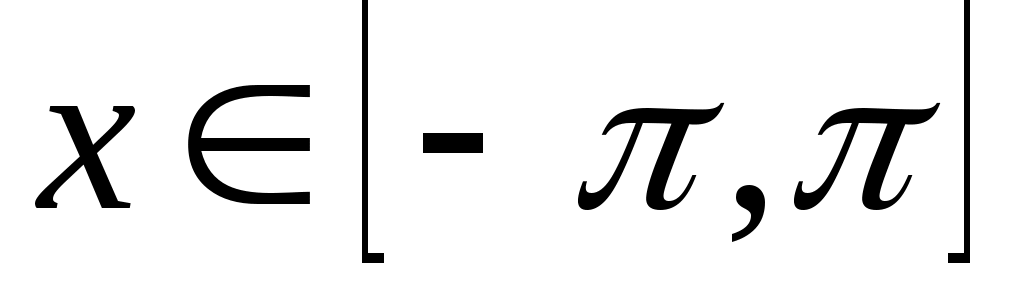 разлагается в ряд Фурье по синусам: разлагается в ряд Фурье по синусам:
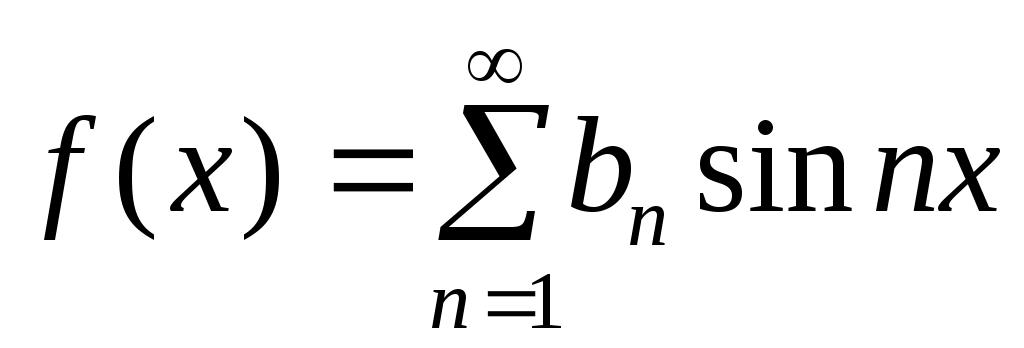 , ,
где 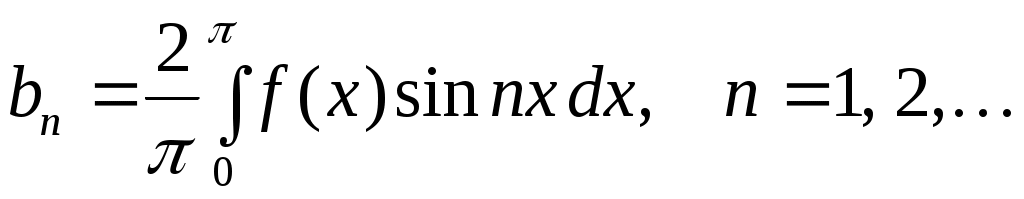 . (5) . (5)
Если 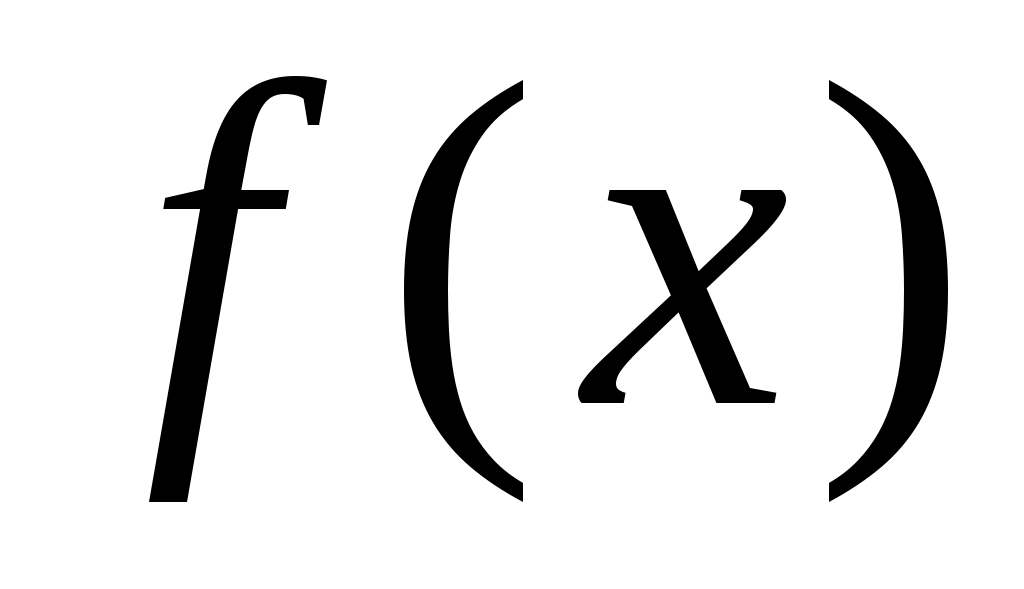 периодическая с периодом периодическая с периодом 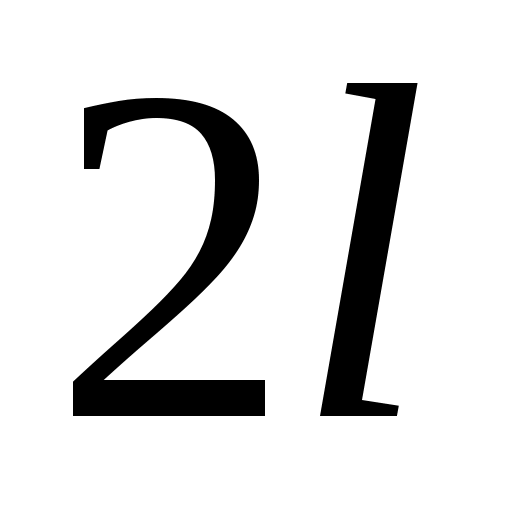 функция, удовлетворяющая условиям теоремы Дирихле на отрезке функция, удовлетворяющая условиям теоремы Дирихле на отрезке 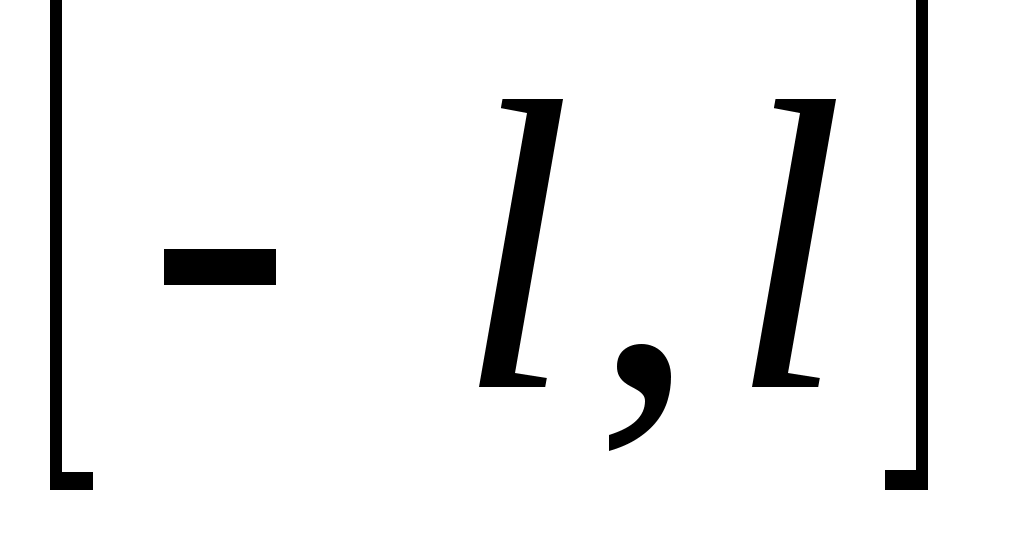 , то ее разложение в ряд Фурье имеет следующий вид: , то ее разложение в ряд Фурье имеет следующий вид:
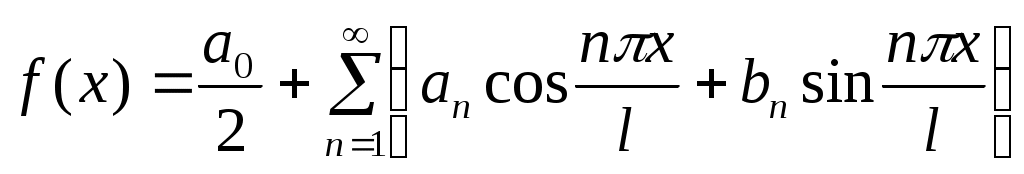 , (6) , (6)
где
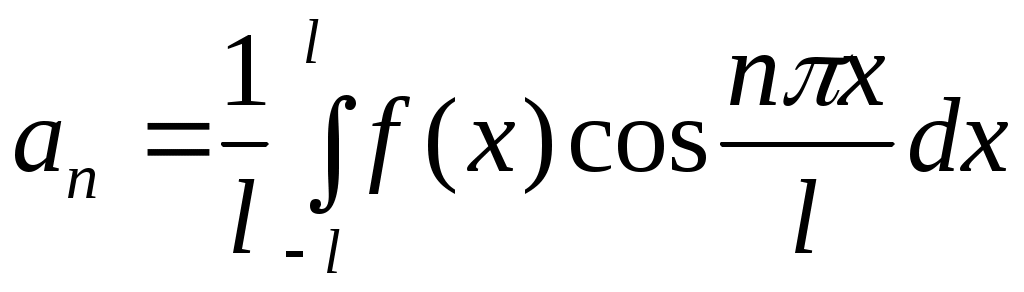 , ,
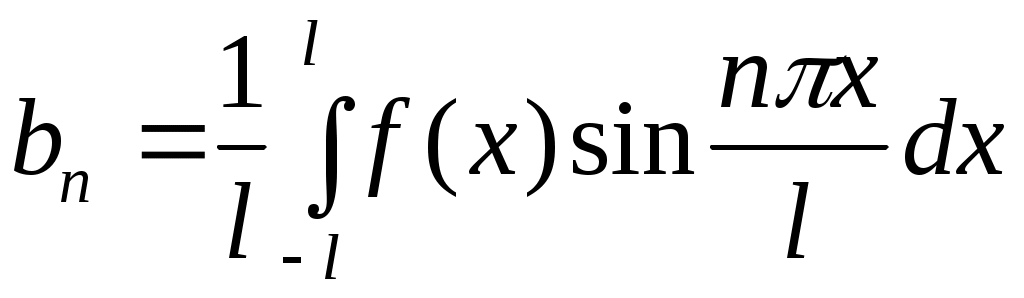 , , 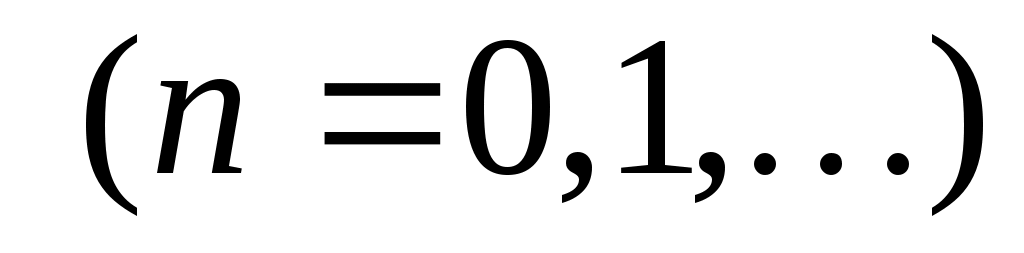 . (7) . (7)
Если 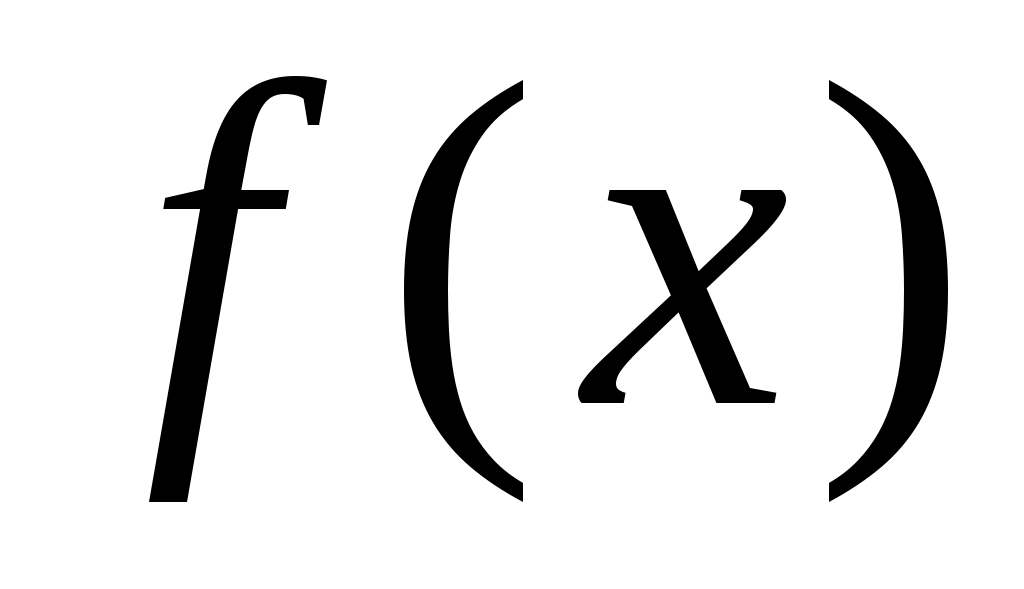 четная функция, то ее ряд Фурье содержит только свободный член и косинусы: четная функция, то ее ряд Фурье содержит только свободный член и косинусы:
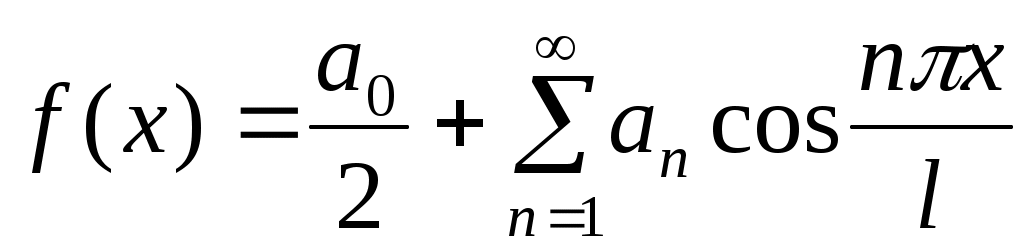 , ,
где
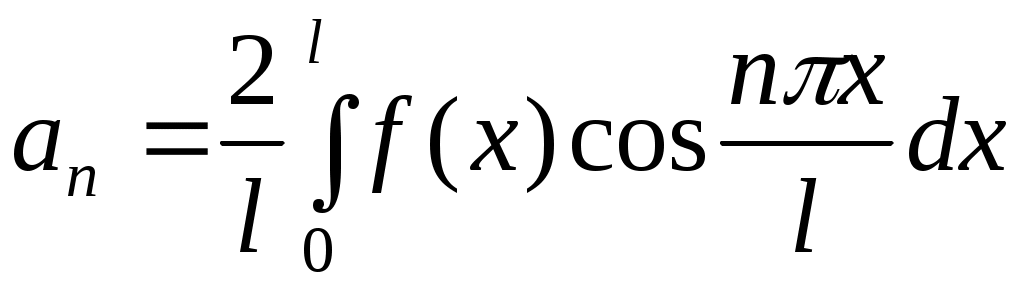 , , 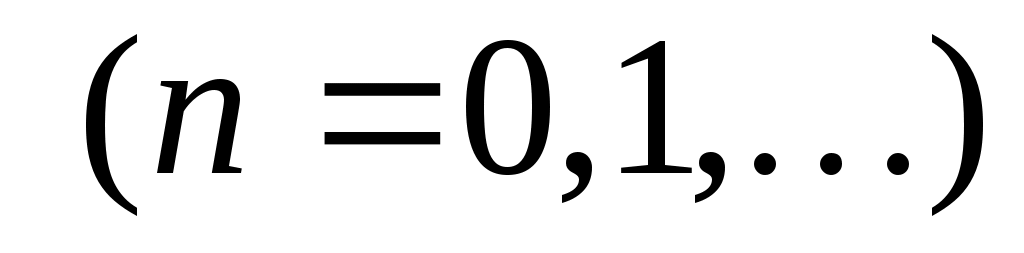 . (8) . (8)
Если 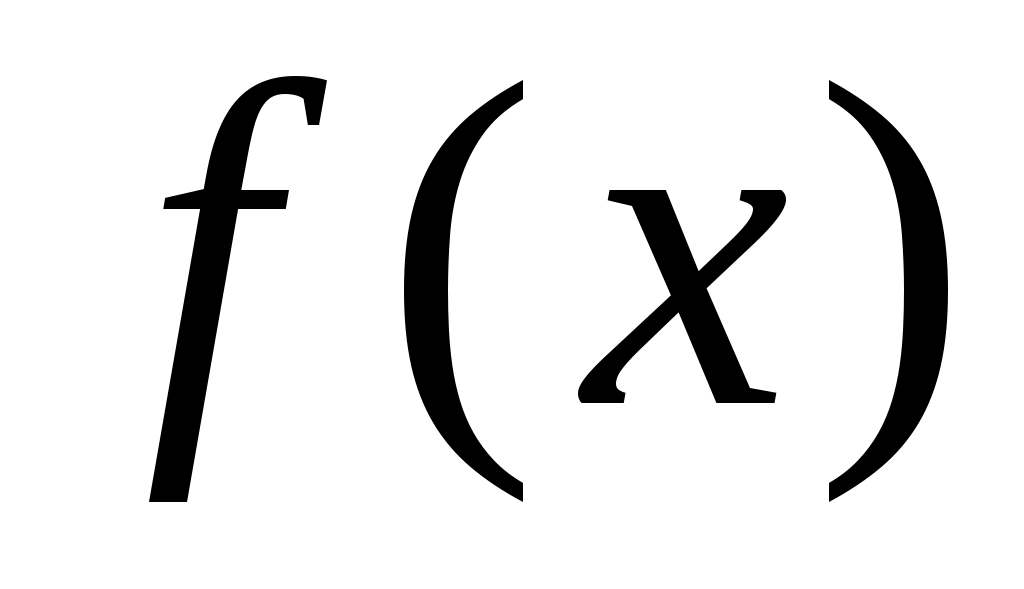 нечетная функция, то ее ряд Фурье содержит только синусы: нечетная функция, то ее ряд Фурье содержит только синусы:
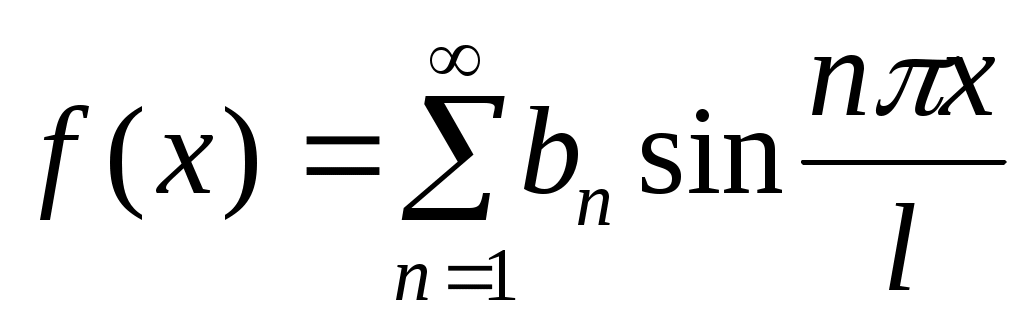 , ,
где
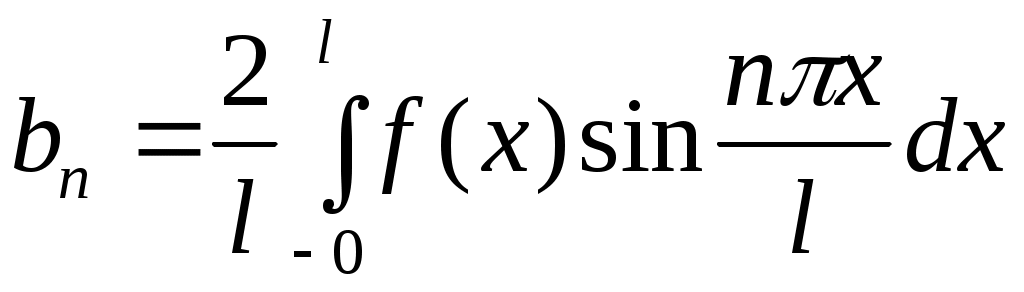 , , 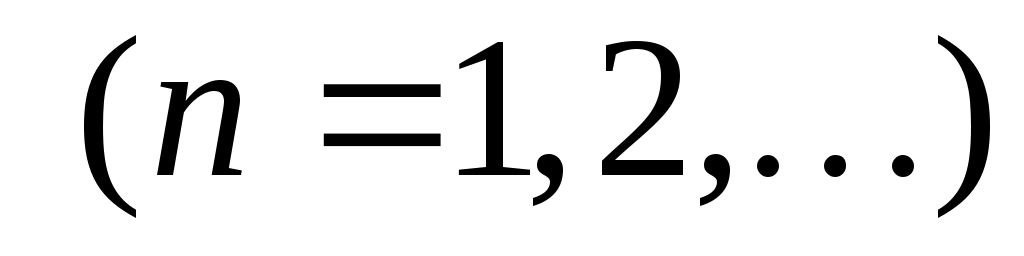 . (9) . (9)
Если функция 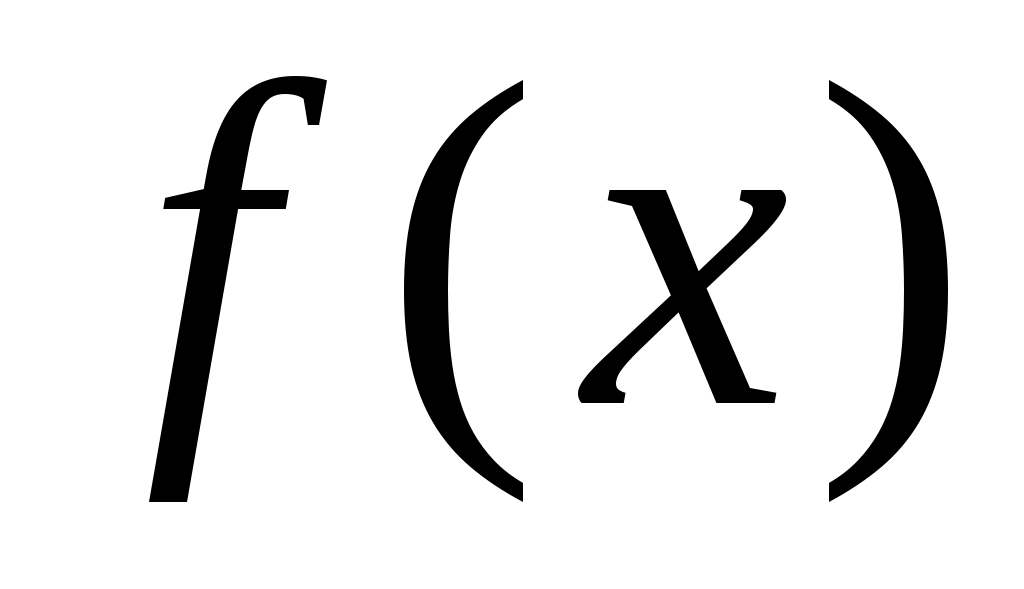 задана на отрезке задана на отрезке 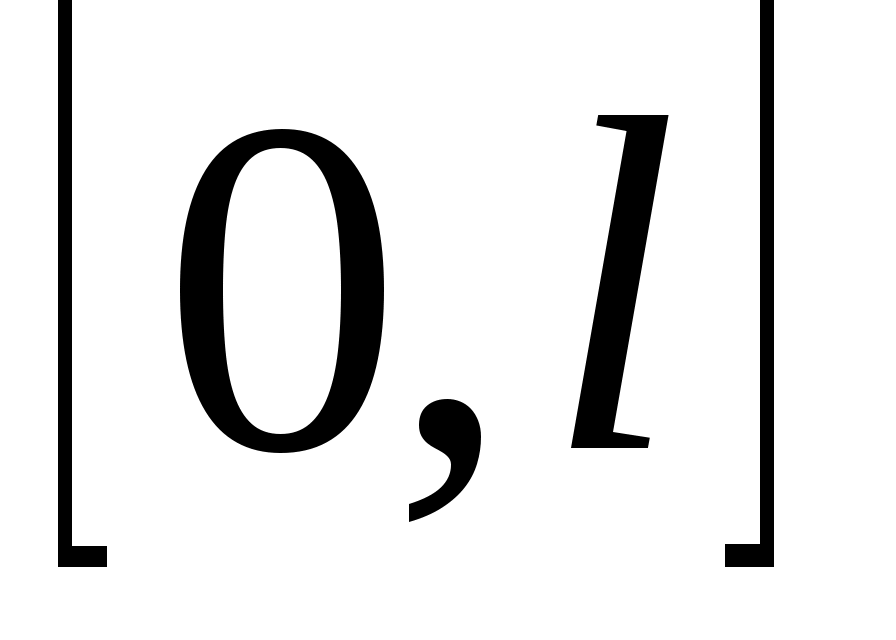 , то для разложения в ряд Фурье достаточно доопределить ее на отрезке , то для разложения в ряд Фурье достаточно доопределить ее на отрезке 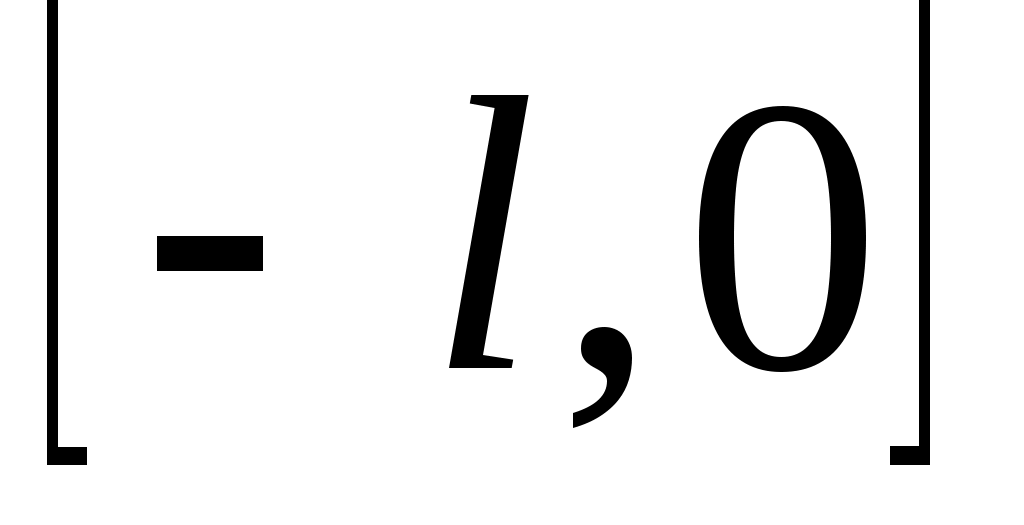 произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на отрезке произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на отрезке 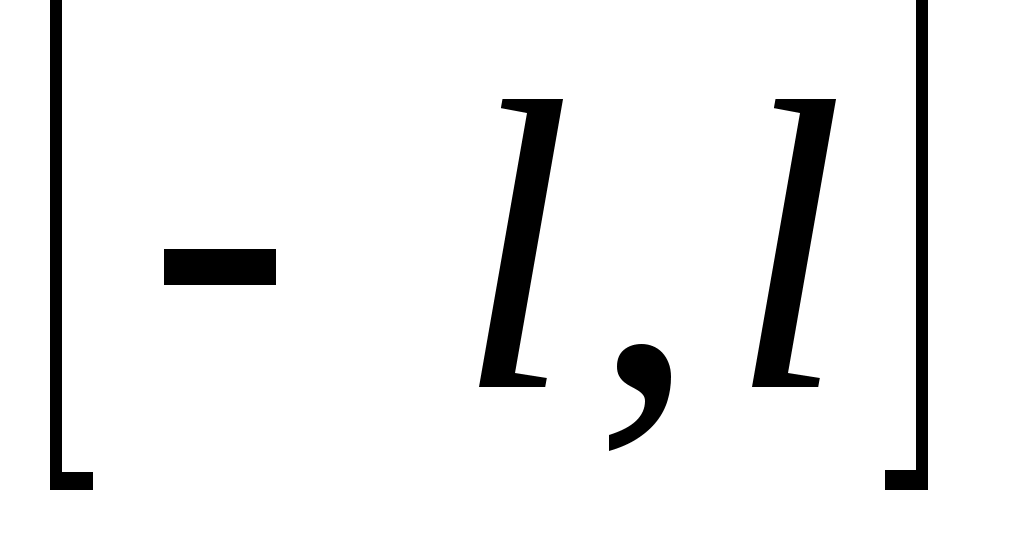 . .
Пример 1. Найти разложение в ряд Фурье периодической функции с периодом 4:
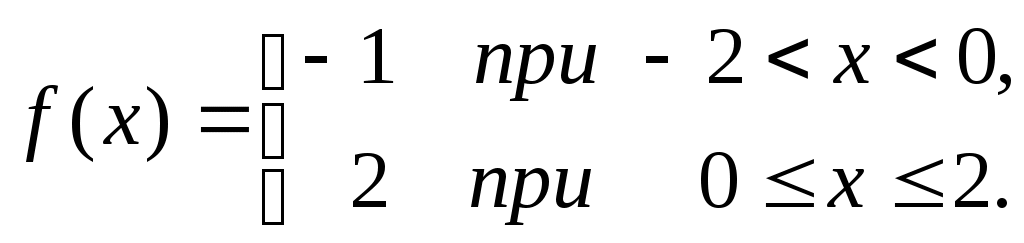
Решение. Функция задана на промежутке длиной 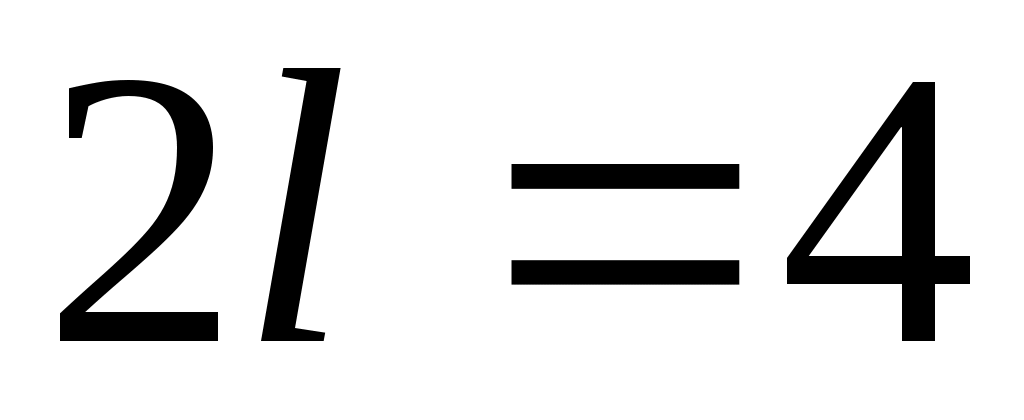 , отсюда , отсюда 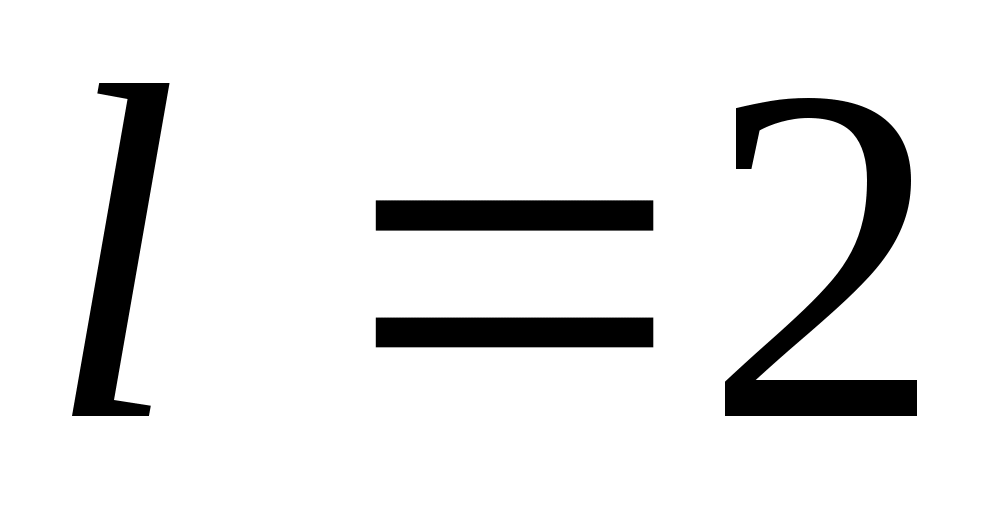 . Находим по формулам 7 коэффициенты ряда: . Находим по формулам 7 коэффициенты ряда:
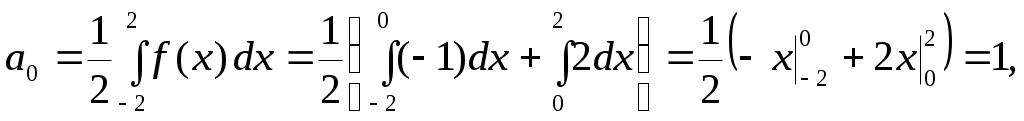
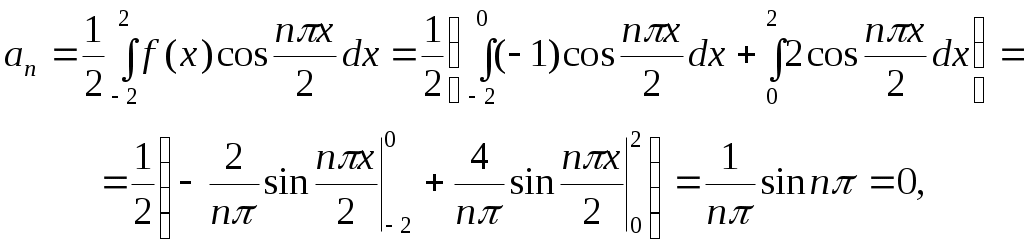
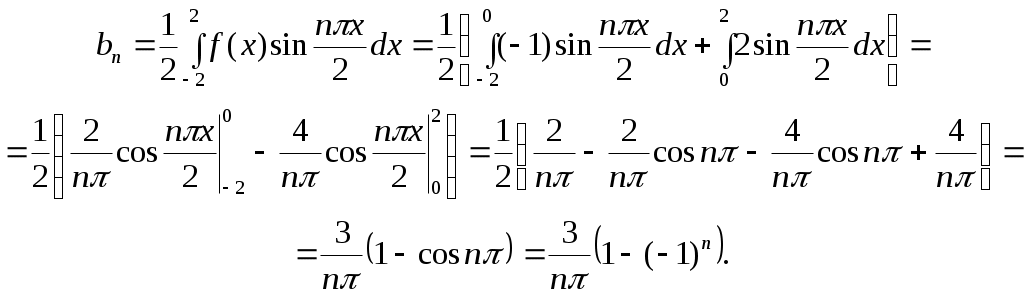 Подставив найденные коэффициенты в ряд 2.26, и учитывая, что при четных значениях Подставив найденные коэффициенты в ряд 2.26, и учитывая, что при четных значениях 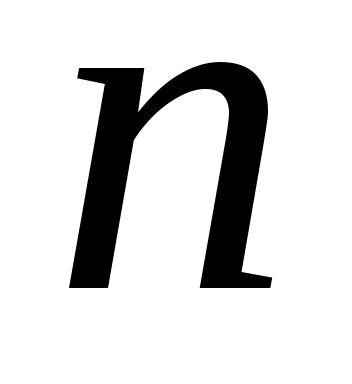 коэффициенты коэффициенты 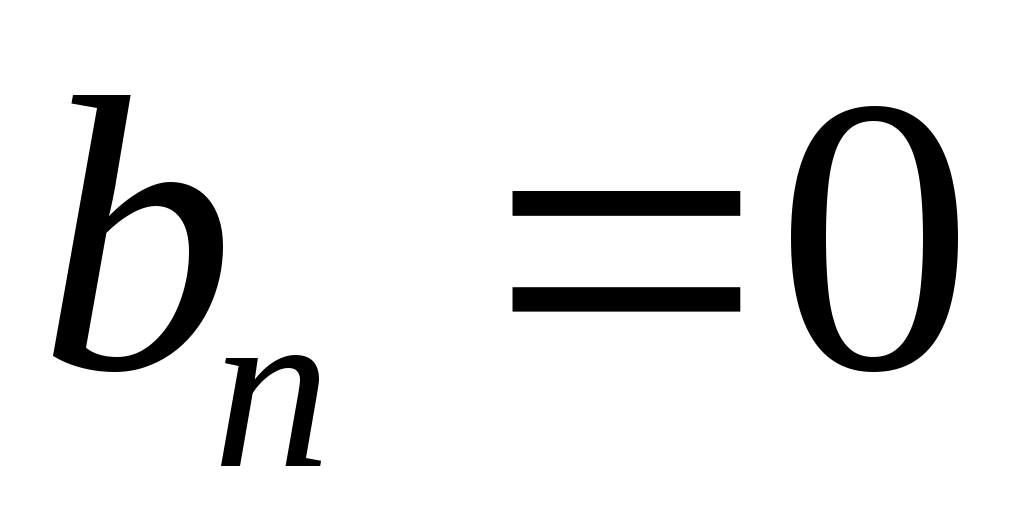 , получим , получим
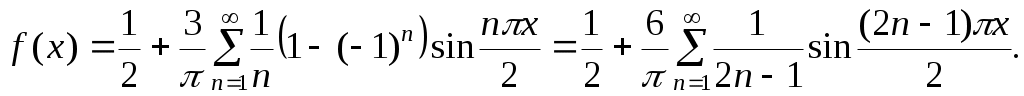
Пример 2.11. Разложить в ряд Фурье функцию, заданную на отрезке 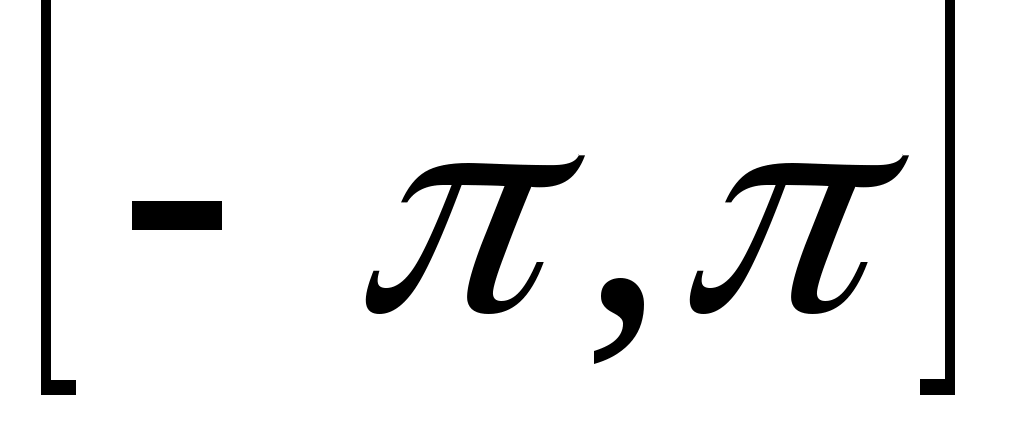 уравнением уравнением 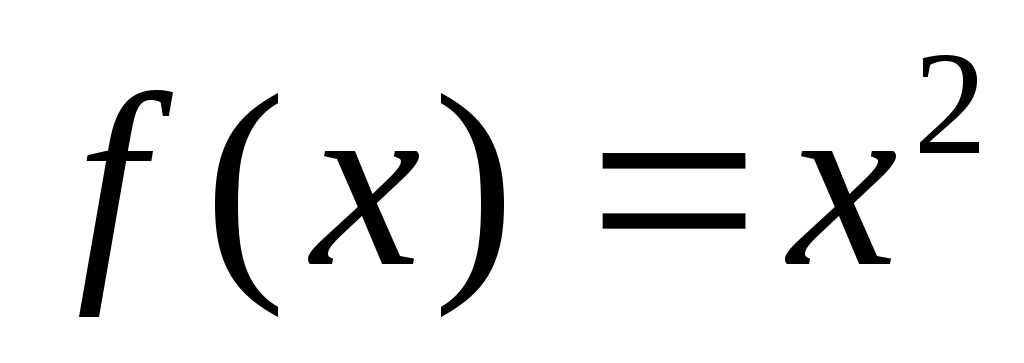 . .
Решение. Рассматриваемая функция является четной, поэтому 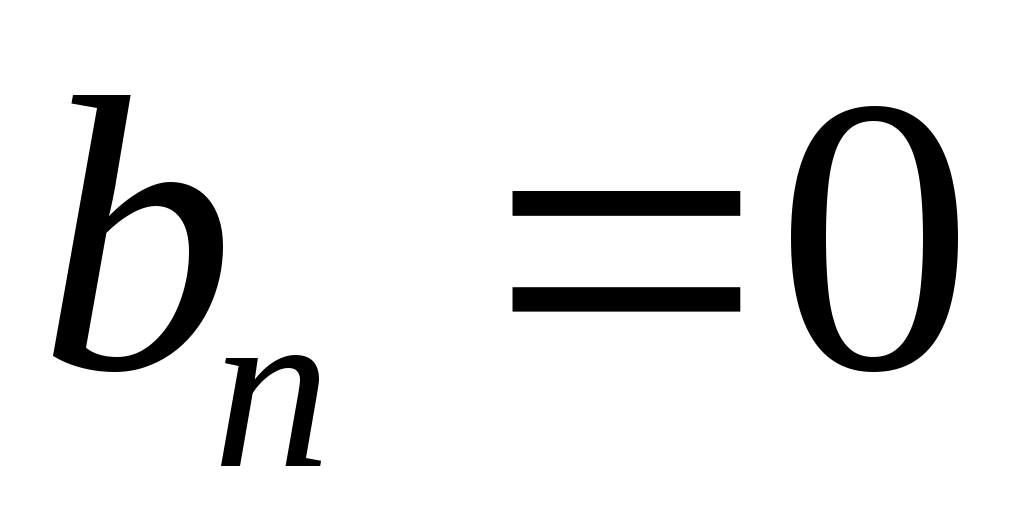 , , 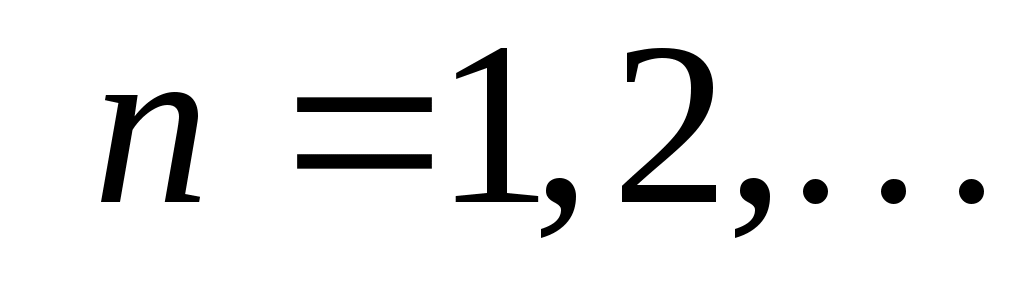 и ряд Фурье имеет вид: и ряд Фурье имеет вид:
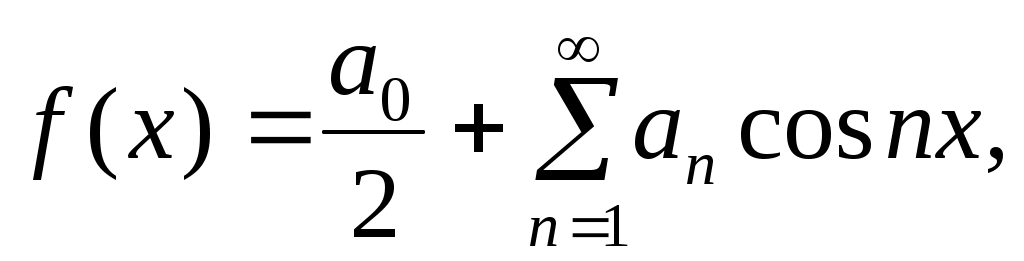
где 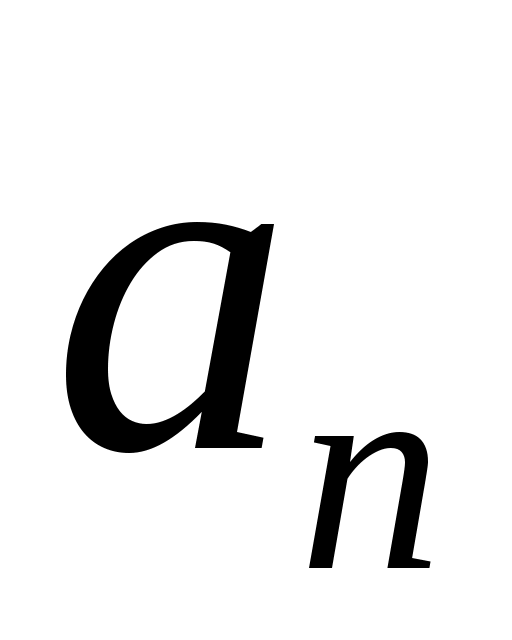 вычисляется по формуле 2.24. вычисляется по формуле 2.24.
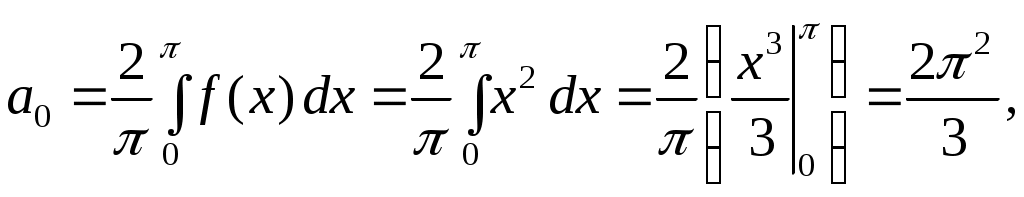
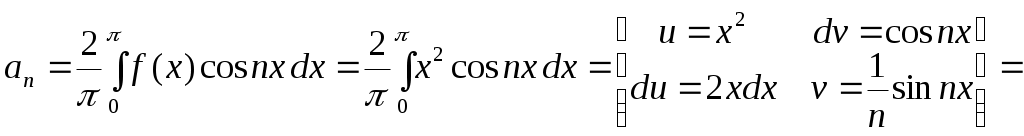
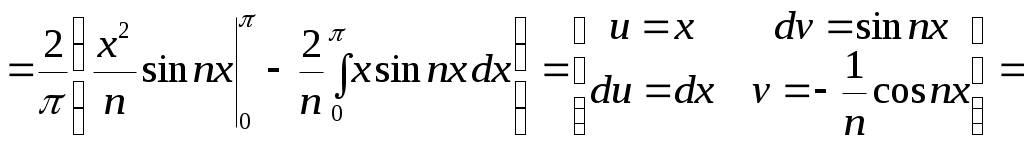
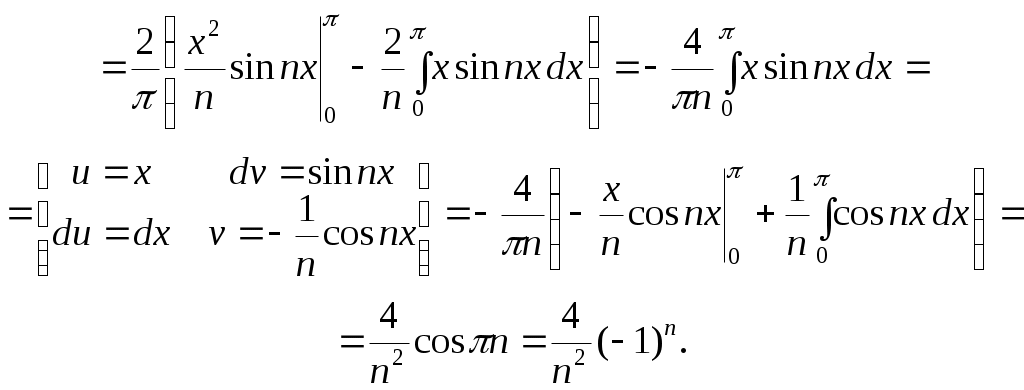
Получаем следующий ряд Фурье для заданной функции на отрезке 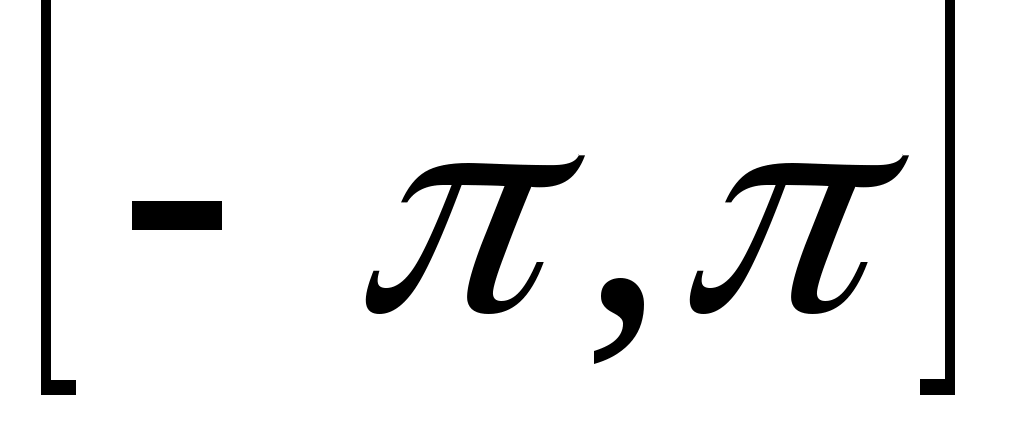 : :
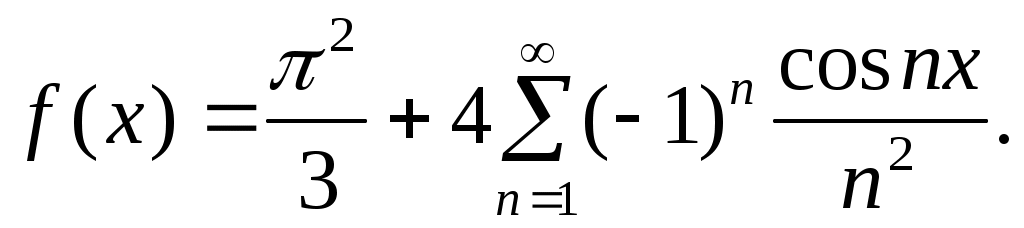 |
|
|
 Скачать 138 Kb.
Скачать 138 Kb.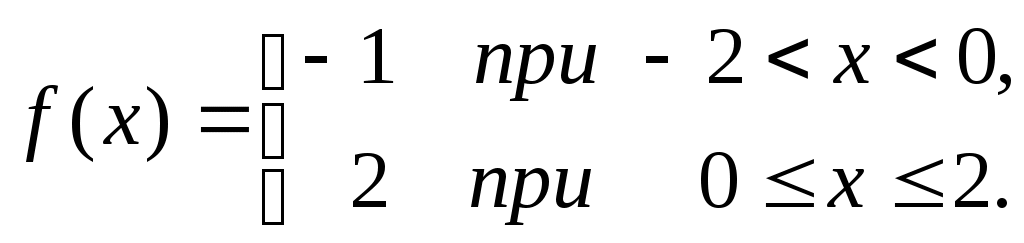
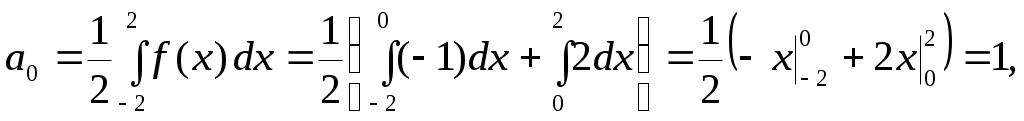
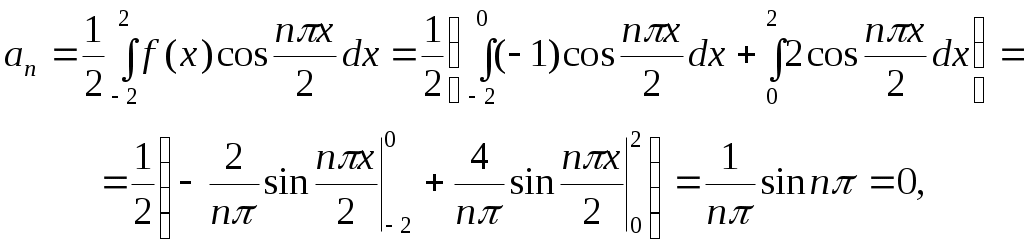
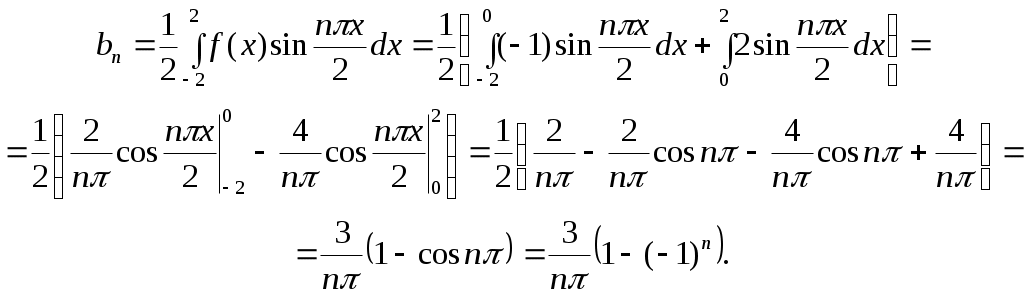 Подставив найденные коэффициенты в ряд 2.26, и учитывая, что при четных значениях
Подставив найденные коэффициенты в ряд 2.26, и учитывая, что при четных значениях