квадрат теңдеу. Квадрат теңдеу. Сабаты таырыбы Квадрат тедеуге келтірілетін жоары дрежелі тедеулер. шінші дрежелі кпмшеге арналан жалпыланан Виет теоремасы
 Скачать 41.89 Kb. Скачать 41.89 Kb.
|
|
Сабақтың тақырыбы: Квадрат теңдеуге келтірілетін жоғары дәрежелі теңдеулер. Үшінші дәрежелі көпмүшеге арналған жалпыланған Виет теоремасы. Сендер квадрат теңдеу және оны шешу тәсілдерін білесіндер. Енді квадрат теңдеуге келтірілетін теңдеулерді шешу жолына тоқталайық.Енді мына теңдеулерді шешіп көріңіздер. х4+ 8х2 - 9=0, x2 + 2x - 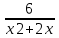 = -5 = -5Бұл теңдеулерді қалай шешеміз, қалай ойлайсыздар? Қандай қиындық туып тұр? Ия, бұл төртінші дәрежелі теңдеу, ендеше бүгінгі тақырыбымыз «Биквадрат теңдеу». Анықтама: ах4 +вх2+с= 0, мұндағы (а≠0), түрінде берілген теңдеу биквадрат теңдеу деп аталады. Нұсқаулық: х4 + 8х2 - 9 =0төртінші дәрежелі теңдеуді шешу үшін жаңа айнымалы енгізіңіз. 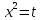 Сонда : 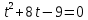 Шыққан квадрат теңдеуді шешіп, түбірлеріңіз табыңыз. Енді х айнымалсының мәнін табу үшін 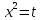 теңдігіне t – ның мәндерін қойыңыз. теңдігіне t – ның мәндерін қойыңыз.Шыққан 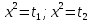 теңдеулерін шешіңіз. теңдеулерін шешіңіз.Жауабы: ______________ Мыс-1: 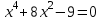 теңдеуін шешейік. теңдеуін шешейік.Шешуі: 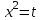 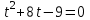 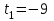   түбірлері болмайды, түбірлері болмайды, 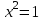 , , 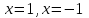 Жауабы: -1;1 Бұл есепте айнымалыны еңгіздік, теңдеуді шешудің мұндай әдісіжаңа айнымалыны еңгізу деп аталады. Квадрат теңдеуге келтіретін теңдеулерді жаңа айнымалы еңгізу әдісімен шешу үшін келесі алгоритмді қолданамыз: Теңдеуге қандай да бір өрнекті жаң айнымалы арқылы белгілейміз; Берілген теңдеудегі өрнектің орнына жаңа айнымалыны еңгізіп, жаңа айнымалыға байланысты квадрат теңдеу аламыз. Шыққан квадрат теңдеуді шешеміз. Алмастыру арқылы алғашқы айнымалының мәнін табамыз; Табылған теңдеулерге тексеру жүргізіп, берілген теңдеудің түбірлерін анықтаймыз. 2- мысалды осы нұсқаулық бойынша өз беттеріңізбен щығарып көріңіздер. Шешуі: ( интерактивті тақтада көрстіледі, оқушылар өз есептерін тексереді) 2-мыс: 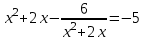 теңдеуін шешіңдер. теңдеуін шешіңдер.Шешуі: 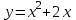 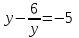 ; ; 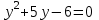 ; ; 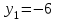 , , 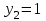 Енді х-тің мәнін табу үшін  және және  екі теңдеу шешеміз. екі теңдеу шешеміз. шешімі жоқ, өйткені шешімі жоқ, өйткені  , ал , ал  түбірлері түбірлері  Жауабы: 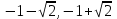 Түсініктерін одан әрі шыңдау мақсатында жұппен тізбектей жұмыстанады, өзара бағалау жүзеге асады. №1. х4 + 5х2 = 126; №2. (х2 - 1)2 –18(х2 - 1) + 45 = 0; №3. 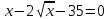 №4. (х2 + 3х - 20)(x2 + 3х + 2) = 240; Жеке жұмыс Мақсат бойыншаоқушылардың қаншалықты деңгейде меңгергендігін бақылау А деңгейі Теңдеуді шешіңіз: а) 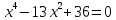 в) 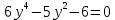 В деңгейі Жаңа айнымалыны енгізу әдісін қолданып теңдеуді шешіңіз: а) 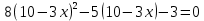 в) 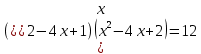 С деңгейі Теңдеуді шешіңіз:  |
