14-1 зертханалық жұмыс. Санды интегралдау
 Скачать 88.53 Kb. Скачать 88.53 Kb.
|
|
Сандық интегралдау у функциясынан х айнымалысы бойынша алынған интегралдың мəнін трапеция əдісімен есептейтін trapz(x,y)функ- циясы кері қайтарады. Мысалы, y xфункциясының интегра- лын 1-ден 2-ге дейінгі аралықта есептейміз:  x=1:0.1:2; y=x; i=trapz(x,y)%сандық интегралдауik=2^2/2-1/2%тексеру Нəтижесі:  » l7_p2i = 1.5 ik = 1.5 Егер функция бір ғана trapz(y)аргументімен шақырылса, онда 1-ге тең интегралдың тұрақты адымы есептеледі (адым- ның туынды мəніне ие болу үшін интегралдың алынған мəнін интегралдаудың адым санына көбейту керек), яғни  x=1:0.1:2; y=x; i=trapz(y)%сандық интегралдауi=i*0.1 ik=2^2/2-1/2%тексеру Нəтижесі:  » l7_p3i = 15 i = 1.5 ik = 1.5 Ал cumtraps(x,y)(cumtraps(y))функциялары қосымша өтпелі нəтижелердің мəнін есептейді. Тікбұрышты импульс түріндегі 8–1242 113 (графикте жуан қызыл түспен бейнеленген) функция үшін cum-trapsфункциясы ізделінген интегралдың жинақталуын көрсететін функцияны көрсетуге көмектеседі. t1туынды уақыт моментіндегі мəні 0-ден t1-ге дейінгі аралықтағы интегралдың мəніне тең. Сценарий мəтіні:  x=0:0.01:3; y=(x<0.5|x>1&x<1.5|x>2&x<2.5);i=cumtrapz(x,y)%сандық интегралдауplot(x,y,'r','LineWidth',3) hold onplot(x,i) Графигі: 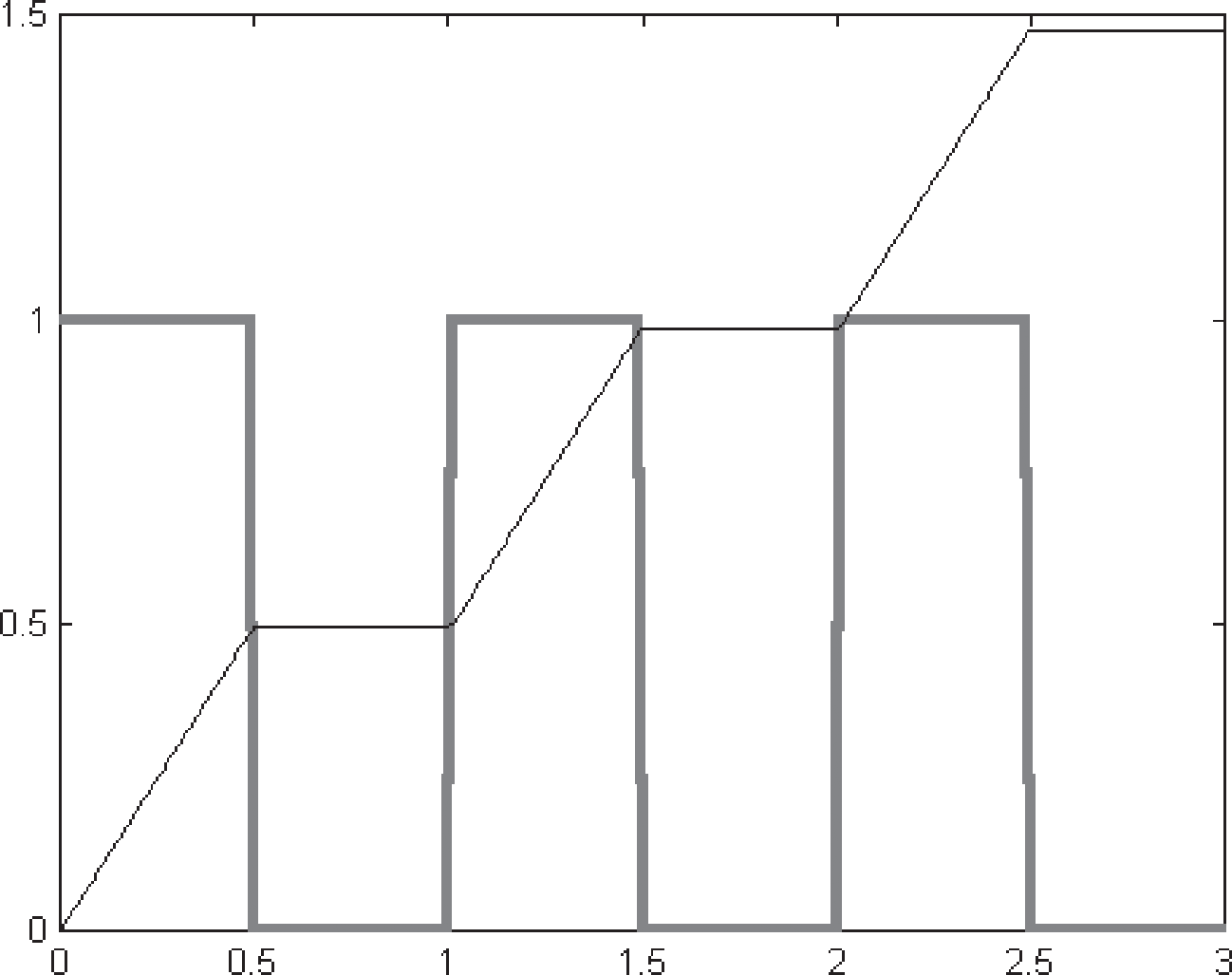 quadжəне quad8функциясы интегралды квадраттау əдісі бойынша есептеуге көмектеседі (quadфункциясы Ньютон-Котес формуласы бойынша екінші реттік болып саналады). Бір типтік функциялар
мұндағы a,b– төменгі жəне жоғарғы интегралдың шектері; tol интегралдаудың салыстырмалы қателігі, тұрақты 1е-3; егер trace 0 – қосымша нақты интеграласты функциясын орындауға қажет; p1,p2,…-интеграласты функциясының параметрлері. /2 Бұл функцияларды қолданайық. Сценарий мəтіні: /2 cos2 (x)dxинтегралын есептеу үшін 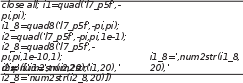 М-функциясы интеграласты өрнегінiң мəнiн есептеу үшiн  function y=l7_p5f(x)y=cos(x).^2; Нəтижесі:  » l7_p5 i1=3.1415926535897931i1_8=3.1415926535897931i2=3.1415926535897931i2_8=3.1415926535897931 Интеграласты функциясының нүктелiк графигi: 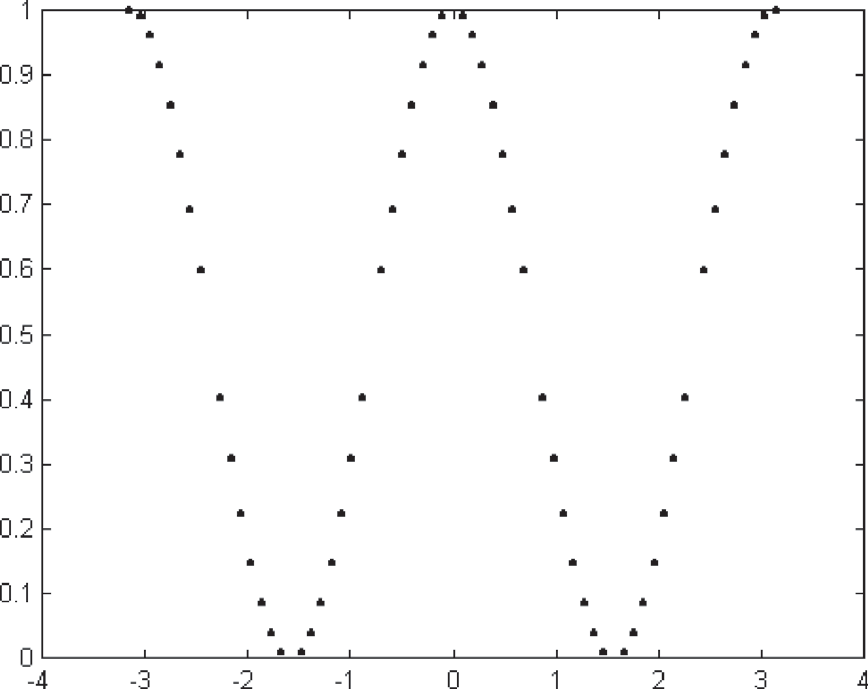 y2 x1 f(x, y)dxdy y1 x1 түрдегі екі еселі интералды шешуді dblquad 
функциясы атқарады. dblquad:dblquad(‘dblquad(‘dblquad(‘ ’,x1,x2,y1,y2) ’,x1,x2,y1,y2,tol) ’,x1,x2,y1,y2,tol, metod) мұндағы ‘функция атауы’ - М-функциясының атауы, интегралас- ты функциясының мəнін береді. Оның екі параметрі болады: біріншісі ішкі интегралдағы айнымалының векторлық мəні, екіншісі сыртқы интегралдағы айнымалының скалярлық мəні. Интегралданатын функция векторды қайтару керек; x1, x2 – ішкі интегралдың төменгі жəне жоғарғы шектері; y1, y2 – сыртқы интегралдың төменгі жəне жоғарғы шектері; 2 Мысалы, sin(x)2 cos(x)2 ydxdy 0 0 интегралының мəнiн таба- мыз. М-функциясының мəтіні:  function f=l7_p6f(x,y)f=sin(x).^2.*cos(x).^2*y; Функцияны шақыру жəне есептеудiң нəтижелерi:  » i=dblquad('l7_p6f',0,pi,0,2*pi)i = 7.75156917007495» i=dblquad('l7_p6f',0,pi,0,2*pi,'quad8')i = 7.75156917007495 Көпмүшелерге |
