ЛАба 3 по тоэ. Санктпетербургский государственный электротехнический
 Скачать 429.54 Kb. Скачать 429.54 Kb.
|
МИНОБРНАУКИ РОССИИСАНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)Кафедра теоретических основ электротехники ОТЧЁТпо лабораторной работе №3 по дисциплине «Теоретические основы электротехники»Тема: Исследование свободных процессов в электрических цепях Студент гр. 0321 Федосеев А.В. Преподаватель Езеров К.С. Санкт-Петербург 2022 Цель работыИзучение связи между видом свободного процесса в электрической цепи и расположением её собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам. Экспериментальные исследования3.2.1. Исследования свободных процессов в цепи первого порядка 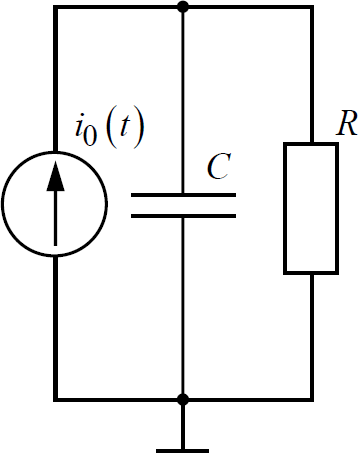 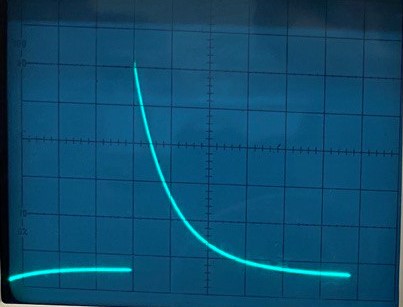 U=0.2V; t=0.1mS C 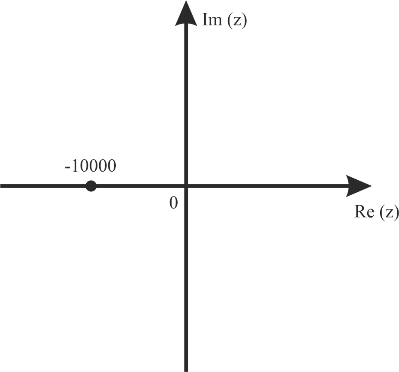 = 0.02 мкФ, R= 5 кОм, TC= 0.6 мс = 0.02 мкФ, R= 5 кОм, TC= 0.6 мс Расчёт по осциллограмме: p1 = 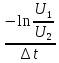 = =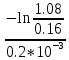 =-9547.71 Гц =-9547.71 ГцТеоретический расчёт:  RC p1 = −α= −1 = 1  − 5·0.02·10 −3 = −10000 Гц Вопросы t Каким аналитическим выражением описывается осциллографируемый процесс? Ответ: Uc = Ae-10000tτ. Соответствует ли найденная собственная частота теоретическому расчёту? Ответ: соответствует с учетом погрешности измерений 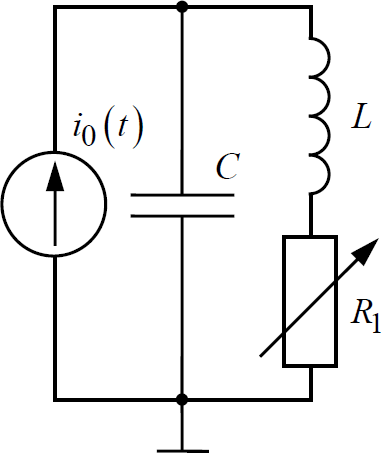  3.2.2. Исследованиесвободныхпроцессоввцепивторогопорядка 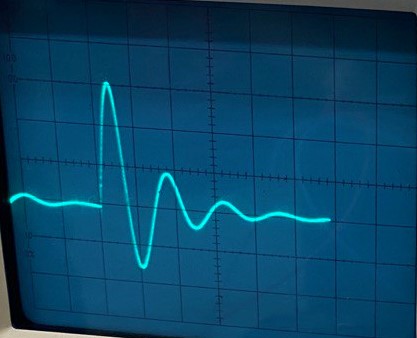 Колебательныйрежим U=0.1V; t=0.1mS Расчёт по осциллограмме: p1,2=-α ± jω= 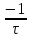 ; α = ; α = 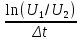 = = 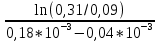 ≈8834.019 Гц. ≈8834.019 Гц.ω = 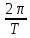 = =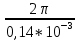 ≈ 44879.9 Гц. ≈ 44879.9 Гц.p1,2 ≈ -8834.0 ± 44879.9*j Гц. Теоретический расчет: C= 0.02 мкФ, L= 25 мГн, R1 = 0.5 кОм p1,2 = -α ± 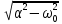 ; ;α = R1/(2L) = 0,5*103/ (2*25*10-3)=10000Гц. 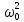 = 1/LC=1/ ( = 1/LC=1/ (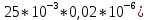 =2* =2*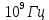 . .p1,2 ≈ -10000±43589*j Гц. 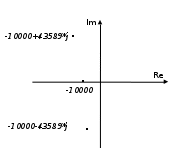 Апериодический режим: 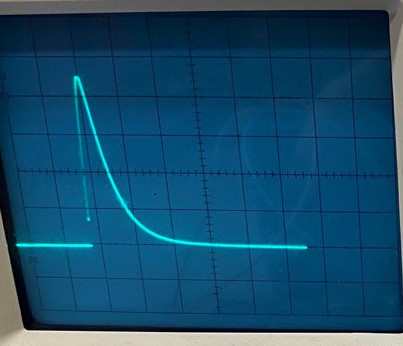 Расчёт по осциллограмме: p1,2=-α ± jω= 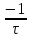 ; α = ; α = 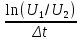 = = 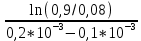 ≈ -17272.21 Гц. ≈ -17272.21 Гц.ω = 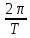 ≈ 62831.84Гц. ≈ 62831.84Гц.p1,2 ≈ -17272.21 ± 62831*j Гц1. Теоретический расчет: C= 0.02 мкФ, L= 25 мГн, R1 = 3 кОм p1,2 = -α ± 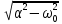 ; ;α = R1/(2L) = 3*103/(2*25*10-3)=60000 Гц. 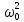 = 1/LC=1/( = 1/LC=1/(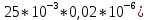 =2 * 109Гц =2 * 109Гцp1,2 ≈ -60000±40000*j Гц. 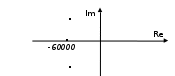 Критическийрежим: 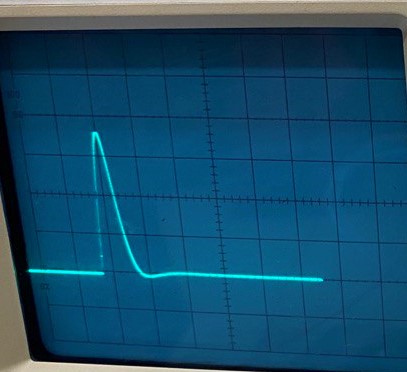 Расчёт по осциллограмме: p1,2=-α =- 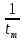 = - = - 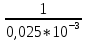 = -40000 с-1. = -40000 с-1.Теоретический расчёт: p1,2 =- α = R1/(2L) = -2*103/(2*25*10-3)= -40000Гц  Добротностьконтуров 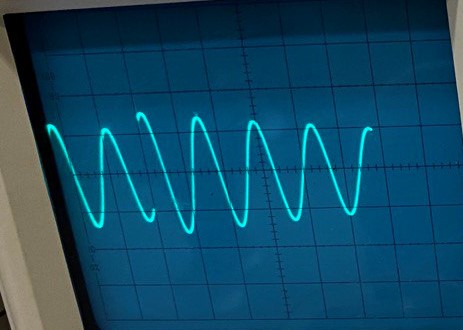 Добротность контура при R1 = 0 Ом. Q= 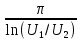 = =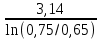 ≈21,94 ≈21,94Добротность контура при R1 = 0,5 кОм. Q= 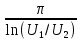 = =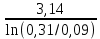 ≈2,54 ≈2,543. Какими аналитическими выражениями (в общем виде) описываются процессы во всех четырёх случаях? Ответ: U(t) = 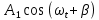 (колебательный режим) (колебательный режим)U(t) = 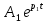 + +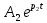 (апериодический режим) (апериодический режим)U(t) = 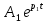 + +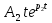 (критический режим) (критический режим)4. Соответствуют ли найденные собственные частоты теоретическому расчёту? Ответ: соответствуют с учетом погрешности измерений. 5. Каковы теоретические значения собственных частот при R1 = 3 кОм и соответствует ли этим значениям снятая осциллограмма? Ответ: Собственная частота цепи по осциллограмме различается от действительной теоретической на относительно значительную величину, вероятная причина износ исследуемой схемы и неточность в измерениях. 6. Как соотносятся найденные значения добротности с результатами теоретического расчёта? Ответ: Теоретическая добротность контура при R1 = 0.5 кОм: Q= 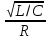 = =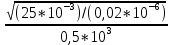 =0,2236…≈ 2,24 =0,2236…≈ 2,24 Сходится с учетом погрешности измерений. Теоретическая добротность контура при R1 = 0 кОм Q = √ L/C R → ∞ при R = 0 Ом колебательный режим должен быть незатухающим, но значение добротности не является бесконечностью, так как цепь имеет некоторое сопротивление и колебания затухают. 3.2.3. Исследованиесвободныхпроцессоввцепивторогопорядка 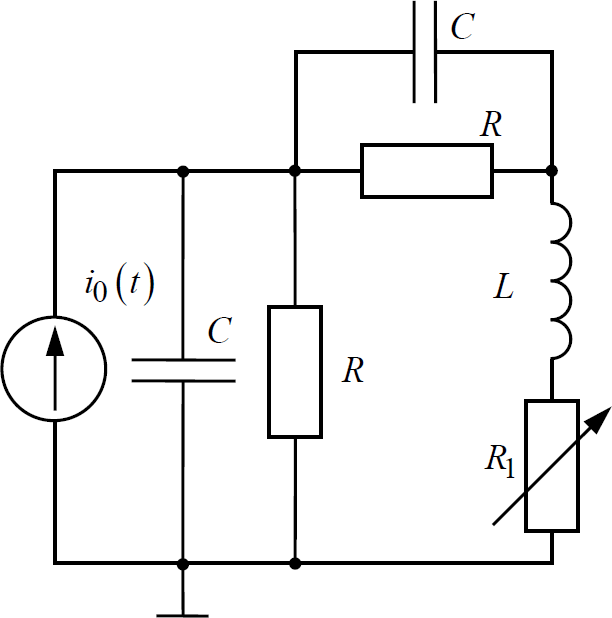 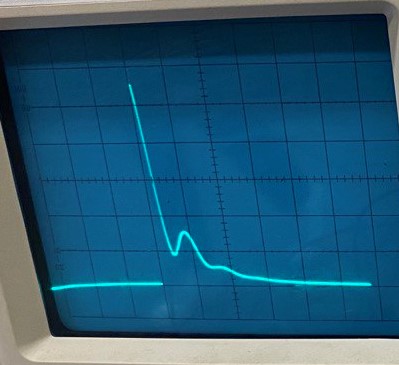 C= 0.02 мкФ, L= 25 мГн, R= 5 кОм, R1 = 1 кОм 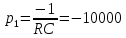 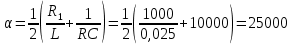 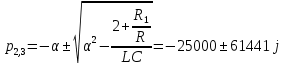 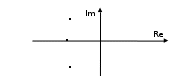 Вопросы: 7. Каким аналитическим выражением описывается осциллографируемый процесс? Ответ: 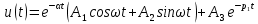 8. Каковы значения собственных частот и соответствует ли этим значениям снятая осциллограмма? Ответ: p1 = −10000, p2,3 = −25000 ± 61441j, осциллограмма соответствует измеренным значениям. ВыводыВ результате выполнения данной лабораторной работы была изучена связь между видом свободного процесса в электрической цепи и расположением её собственных частот на комплексной плоскости; экспериментально определены собственные частоты и добротность RLC-контура по осциллограммам. Составлены диаграммы расположения собственных частот цепи на комплексной плоскости, обработаны осциллограммы свободных процессов в цепях. Большинство теоретических выкладок совпадают с экспериментальными значениями с учетом погрешности измерений. |
