Сбор и подготовка скважинной продукции. Сбор и подготовка скважинной продукции
 Скачать 2 Mb. Скачать 2 Mb.
|
10.1.1. Гидравлический расчетЗначение коэффициента гидравлического сопротивления рассчитывается в зависимости от режима движения газа и шероховатости труб по тем же формулам, что и для нефтепровода. Для гидравлических гладких труб не зависит от шероховатости внутренней поверхности трубы и рассчитывается по формуле: =0.067(158/Re)0.2=0.1844/ Re0.2 (143) При квадратичном режиме течения не зависит от Re, и является функцией относительной шероховатости: =0.067(2/d)0.2 (144) По универсальной формуле ВНИИ газа: =0.067(158/Re+2/d)0.2 (145) Значение числа Re для смеси газов: 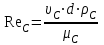 , (146) , (146)где С=у11+ у22+…+ уnn – вязкость смеси газов; i – вязкость отдельных компонентов газа, кг/мс; уi – объемная доля компонента в составе газа; С – плотность смеси газов в условиях трубопровода, кг/м3. 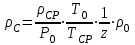 , (147) , (147)где 0 – плотность смеси газов при Н.У., кг/м3; Рср и Р0 – соответственно среднее давление в трубопроводе и барометрическое, Па; ТСР и Т0 – соответственно средняя температура перекачки и температура абсолютного нуля (273.15). 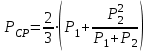 . (148) . (148)Упрощение: по данным ВНИИ газа для новых труб =0.03мм. Тогда из (144): =0.03817/d0.2. (149) При технических расчетах (с учетом местных сопротивлений) можно принимать =(1.03-1.05)ТР. (150) Обычно течение газа происходит при высоких скоростях, когда сопротивление определяется только шероховатостью труб (квадратичная зона). Т.к. шероховатость не зависит от диаметра трубопровода, можно считать, что зависит только от диаметра газопровода. Одной из формул типа = (d), получившей широкое распространение, является формула Веймаута: =0.009407/ 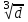 (151) (151)Формула Веймаута (151) может использоваться при ориентировочных расчетах диаметра и пропускной способности простого газопровода. В этом случае расчетные формулы имеют вид: 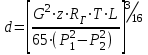 , (152) , (152)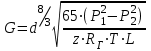 . (153) . (153)Из формулы (142) можно получить выражение для определения длины L, диаметра d и конечного давления Р2 при известном начальном Р1: 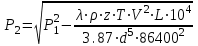 . (154) . (154)10.1.2. Изменение температуры газа по длине газопровода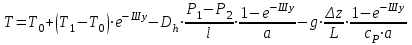 (155) (155)где a=kD/GCCP; Т1 – начальная температура газа; L – расстояние до рассматриваемой точки; Dh – коэффициент Джоуля-Томсона, К/МПа. Первое слагаемое характеризует внешний теплообмен, второе – изменение температуры газа за счет эффекта Джоуля-Томсона, третье – изменение температуры газа в зависимости от его положения по высоте газопровода. Как следует из этого уравнения, за счет эффекта Джоуля-Томсона температура транспортируемого реального газа может быть даже ниже температуры окружающего грунта. Когда эффект Джоуля-Томсона не учитывается, Dh=0, и считается, что газопровод горизонтальный, z=0, из этого уравнения непосредственно следует формула Шухова для расчета температуры газа в трубопроводе. При расчете по формуле Шухова температура газа никогда не может быть ниже температуры грунта. При отсутствии внешнего теплообмена между газом и грунтом, т.е. в условиях идеальной теплоизоляции газопровода, температура транспортируемого газа изменяется только за счет эффекта Джоуля-Томсона и изменения положения центра тяжести потока. Отмеченные особенности течения реального газа по газопроводу указывают на необходимость учета эффекта Джоуля-Томсона при определении температуры транспортируемого газа по длине газопровода.  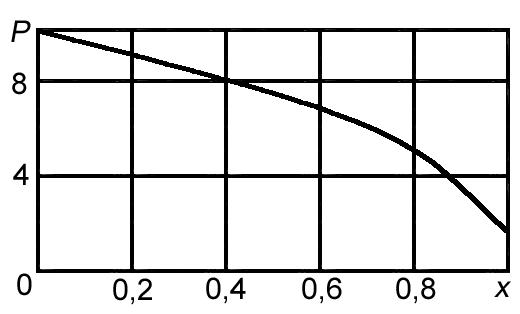 Рис.32. Изменение давления по длине газопровода 10.1.3. Изменение давления по длине газопровода Требуется определить давление в любой точке на расстоянии Хот начала газопровода. Записав по формуле (138) для двух участков газопровода (от его начала до т. Х и от т. Х до конца газопровода) массовые расходы газа и, учитывая постоянство расхода по длине газопровода, приравняем правые части уравнения, получим: 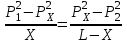 , (156) , (156)Откуда 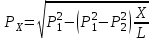 . (157) . (157)Отсюда следует, что давление по длине газопровода уменьшается по параболическому закону (рис.32). Из характера кривой вытекает, что по длине газопровода градиент давления 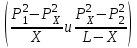 постепенно увеличивается, т.е. гидравлический уклон не является постоянным. постепенно увеличивается, т.е. гидравлический уклон не является постоянным.В начале газопровода, когда давление и плотность газа высокие, а удельный объем газа ( 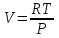 ) мал, потери давления в газопроводе незначительны, т.е. градиенты давления малы. По мере удаления газа от начала трубопровода давление падает, а удельный объем газа увеличивается, что приводит к увеличению скорости движения газа и, соответственно, росту потерь давления на трение, пропорциональных квадрату скорости (уравнение Дарси-Вейсбаха). ) мал, потери давления в газопроводе незначительны, т.е. градиенты давления малы. По мере удаления газа от начала трубопровода давление падает, а удельный объем газа увеличивается, что приводит к увеличению скорости движения газа и, соответственно, росту потерь давления на трение, пропорциональных квадрату скорости (уравнение Дарси-Вейсбаха).Т.к. в газопроводах закон падения давления по длине имеет нелинейный характер, то среднее давление определяется как среднеинтегральное (148). |
