Сбор и. Сбор и подготовка скважинной продукции
 Скачать 3.83 Mb. Скачать 3.83 Mb.
|
1.8.3. Расчет гравитационного сепаратора на пропускную способность по газу и жидкости1.8.3.1. Расчет количества газа, выделившегося по ступеням сепарацииСуммарное количество газа (свободного и растворенного), содержащегося в нефти и поступающего на первую ступень сепарации, определяется по формуле: Количество газа, оставшегося в растворенном состоянии в нефти VР и поступающего из первой ступени во вторую, согласно закону Генри, равно: Дебит отсепарированного газа на первой ступени будет равен: Дебит свободного газа, отсепарированного на второй ступени, будет равен: Обозначения: VГ - количество газа, поступающего из скважины, м3/сут; Г - газовый фактор, м3/ м3; QН - дебит нефти, м3/сут; V1, V2…- количество газа, сепарируемого соответственно при давлениях Р1, Р2…, м3/сут; α- коэффициент растворимости газа в нефти при температуре и давлении в сепараторе, м2/н; Р1, Р2…- давления на первой, второй и т.д. ступенях сепарации, Па. Коэффициент растворимости газа в нефти α при давлениях выше 9,81×105 Па (10 кГс/см2) обычно изменяется линейно. Величины α для давлений сепарации меньших 10 кГс/см2, будут сильно зависеть от давления. Поэтому для точных определений необходимо иметь кривую изменения α от давления, построенную на основе анализа глубинной пробы нефти соответствующей скважины. 1.8.3.2. Расчет вертикального гравитационного сепаратора по газуЕще до входа в сепаратор газ, выделившийся из нефти в результате снижения давления, представляет полидисперсную систему, в которой собственно газ является дисперсионной средой, а частицы нефти (и воды при наличии ее в продукции скважины), диспергированные в газе - дисперсионной фазой. Такую дисперсную систему называют аэрозолем. В сепараторе диспергирование нефти увеличивается вследствие расширения потока, удара нефти о внутренние поверхности нефтегазового сепаратора и расширения газа. Вследствие этого в сепарационной и осадительной секциях дисперсность системы увеличивается. Частицы дисперсной фазы имеют различные размеры - от характерных для тумана и пыли до более крупных. Последние относительно быстро опускаются вниз вместе с основной массой нефти, более мелкие могут образовывать псевдоожиженный или кипящий слой различной высоты, а самые мелкие частицы увлекаются потоком газа из нефтегазового сепаратора. Осаждение частиц из газа в гравитационном сепараторе происходит в основном по двум причинам: вследствие резкого снижения скорости газового потока и вследствие разности в плотностях газовой и жидкой (твердой) фаз. Для эффективной сепарации необходимо, чтобы расчетная скорость движения газового потока в сепараторе была меньше скорости осаждения жидких и твердых частиц, движущихся под влиянием силы тяжести во встречном потоке газа, т.е. Высокую степень очистки газа от капельной и твердой взвеси в гравитационном сепараторе можно получить при условии, что скорость газа будет близка к нулю. В реальных условиях эффективность сепарации в гравитационных сепараторах при скорости движения газа более 0,5 м/сек резко падает и составляет лишь 70% капельной жидкости, находящейся во взвешенном состоянии. Практика эксплуатации гравитационных сепараторов показала, что оптимальной скоростью газа является 0,1 м/с при давлении 5,87 МПа/м2 (60 кГс/см2). Пропускную способность гравитационных сепараторов обычно определяют в зависимости от допустимой скорости движения газа, при которой происходит осаждение капелек жидкости минимального размера, принятого для расчета. Допустимая скорость движения газа WГ определяется из условия равновесия сил, действующих на частицу, и силы сопротивления среды, возникающей при движении этой частицы. При расчете гравитационных сепараторов по газу принимаются следующие допущения: 1) частица (твердая или жидкая) имеет форму шара; 2) движение газа в сепараторе установившееся, т.е. такое, когда скорость газа в любой точке сепаратора независимо от времени остается постоянной, но по абсолютному значению может быть разной; 3) движение частички принимается свободным, т.е. на нее не оказывают влияние другие частицы; 4) скорость оседания частицы постоянная, это тот случай, когда сила сопротивления газовой среды становится равной массе частицы. Исходя из принятых допущений, рассмотрим силы действующие на частицу, осаждающуюся в газовой среде: 1) где m - масса частицы; g - ускорение силы тяжести, м/с2; ρч - плотность частицы. Поскольку частица шарообразна, ее объем равен где d - диаметр частицы. Тогда : 2) Силу сопротивления газа R при свободном оседании частицы можно представить в следующем виде: где ξ - коэффициент сопротивления среды, являющийся функцией критерия Рейнольдса; ρГ - плотность газа, кг/м3; WЧ - линейная скорость частицы, м/с; SЧ - площадь сечения частицы, π·d2/4. 3) Исходя из 4-го допущения, в момент, когда R уравновесит силы тяжести и частица будет двигаться равномерно FТЯЖ - FА- R = 0, (14) ускорение равно нулю. Т.е. исходя из равновесия сил, действующих на частицу, можно записать: Р = R. Отсюда: Из этого уравнения можно определить коэффициент сопротивления ξ: 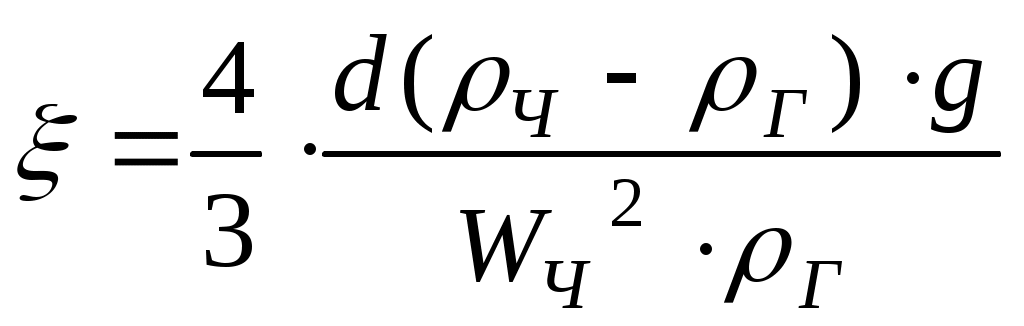 . (16) . (16)Для ламинарного движения частиц (Rе < 2) коэффициент сопротивления рассчитывается по формуле: где νг - кинематическая вязкость газа: т.е. сопротивление среды пропорционально вязкости; μг - динамическая вязкость газа, Если подставить (5) и (5') в формулу (4) для ξ: 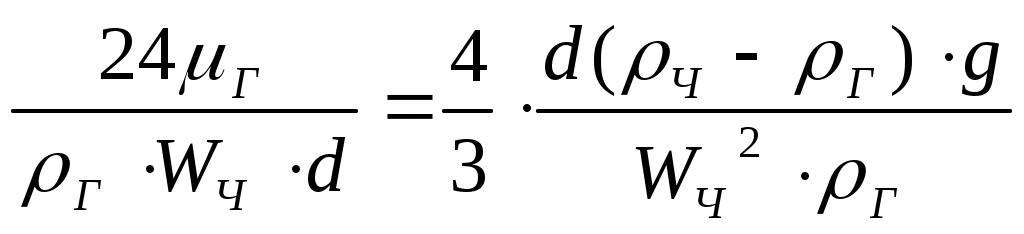 , (19) , (19)то отсюда можно получить уравнение для расчета скорости оседания шарообразной частицы в газовой среде (формула Стокса): 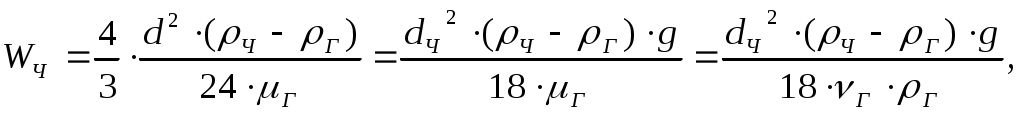 (20) (20)где μг - динамическая вязкость газа, d - диаметр частицы, м; ρч – плотность частицы в условиях сепаратора, кг/м3; νг- кинематическая вязкость газа в условиях сепаратора, м2/с. В промысловых сепараторах Rе для частицы значительно выше, чем 2. При значениях числа Rе от 2 до 500 зависимость коэффициента сопротивления ξ представляется эмпирическим уравнением: Подставляя данное уравнение в формулу (4), получаем формулу Аллена: 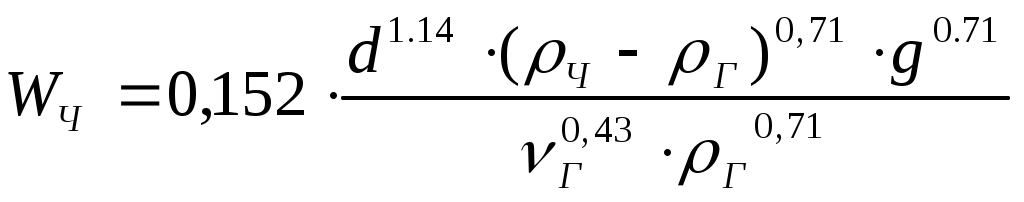 , (22) , (22)из которой следует, что влияние вязкости среды на скорость оседания частицы снижается. Для турбулентного режима движения при значениях числа Rе более 500 (до 2·105), коэффициент сопротивления ξ для шарообразной частицы становится постоянным и равным 0,44. Подставляя это значение в формулу (16), получим уравнение Ньютона-Ритингера: из которого следует, что вязкость среды не оказывает влияния на скорость оседания частицы. Как определить скорость потока газа? Пропускная способность вертикального сепаратора по газу определяется в зависимости от допустимой скорости движения газа: где V- пропускная способность по газу при Н.У., т.е.: P0 = 1,033 . 9,81·104, Па = 1,01·105, Па = 0,1013 МПа; Т0 = 273 К; D - внутренний диаметр сепаратора, м; Р - давление в сепараторе, Па; Т - абсолютная температура в сепараторе, К; Z - коэффициент, учитывающий отклонение реального газа от идеального при рабочих условиях в сепараторе. WГ - скорость подъема газа в вертикальном сепараторе, м/с. Отсюда: Итак, выпадение частицы происходит при условии WЧ - WГ > 0. На практике при расчетах применяется Подставив выражения скоростей в данное уравнение, получаем: 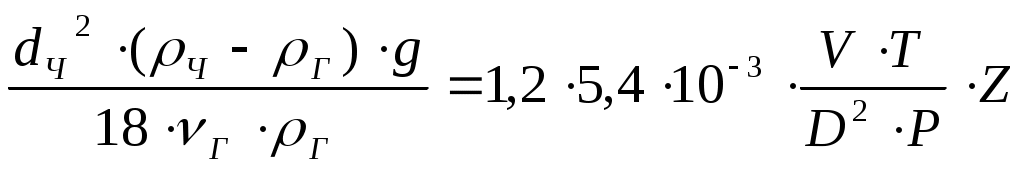 (27) (27)или 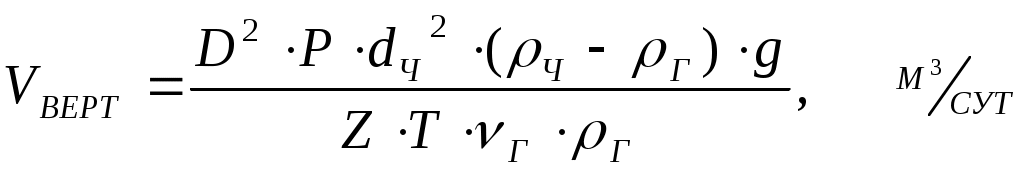 (28) (28)По этой формуле можно определить пропускную способность V вертикального сепаратора, если задаться минимальным диаметром капелек жидкости d, которые будут осаждаться при выбранных условиях (Р, Т), и диаметром сепаратора D. Обычно принимают d = 10- 4 м. |
