книга заданий пайтон. книга практических заданий, pyton. Сборник упражнений Введение в язык Python с задачами и решениями Бен Стивенсон Москва, 2021 удк 004. 438Python
 Скачать 2.24 Mb. Скачать 2.24 Mb.
|
8.2. числа фиБоначчиЧислами Фибоначчи называется последовательность целых чисел, начинающаяся с нуля и единицы, в которой каждое последующее ее значение равно сумме двух предыдущих. Таким образом, первые десять чисел Фибоначчи будут следующие: 0, 1, 1, 2, 3, 5, 8, 13, 21 и 34. Последовательность чисел Фибоначчи обычно обозначается как Fn, где n – неотрицательное целое число, определяющее индекс элемента в последовательности (начиная с 0). Числа Фибоначчи, не считая первых двух, можно легко вычислить по формуле Fn = Fn–1 + Fn–2. Данное определение рекурсивно по своей природе, поскольку каждое следующее число ряда Фибоначчи вычисляется на основе предыдущих чисел из этой последовательности. Первые два числа ряда F0 и F1 представляют собой базовые случаи рекурсии, так как имеют постоянные значения, не рассчитываемые на основании предыдущих элементов. Универсальная программа для рекурсивного расчета чисел Фибоначчи представлена ниже. В ней вычисляется и отображается значение Fn для n, введенного пользователем. # Рассчитываем n–е число ряда Фибоначчи # @param n – индекс искомого числа Фибоначчи # @return значение n–го числа Фибоначчи def fib(n): # Базовые случаи if n == 0: return 0 if n == 1: return 1 # Рекурсивный случай return fib(n–1) + fib(n–2) # Рассчитываем число Фибоначчи, запрошенное пользователем n = int(input("Введите неотрицательное число: ")) print("fib(%d) равно %d." % (n, fib(n))) Это очень компактный рекурсивный алгоритм поиска чисел Фибоначчи, но у него есть минус – он не так быстр, особенно когда речь идет о больших значениях. И если fib(30) на средненьком по мощности компью тере выполнится довольно быстро, то fib(70) потребует в разы больше времени. Так что большие числа Фибоначчи обычно вычисляются при помощи цикла или формулы. Из этого вы могли бы сделать вывод, что алгоритмы, включающие в себя рекурсию, обязательно будут медленными. И хотя в данном конкретном случае это так, в целом подобное утверждение далеко от истины. Наша предыдущая программа, суммирующая целые числа, работала быстро даже для больших значений, а есть и другие задачи, которые быстро и элегантно решаются при помощи рекурсивных алгоритмов. Среди таких задач – алгоритм Евклида, представляющий собой эффективный способ нахождения наибольшего общего делителя двух целых чисел. Подробнее о нем мы поговорим в упражнении 174. На рис. 8.1 схематически показано количество вызовов функций при вычислении числа Фибоначчи для n, равного 4 и 5, и аналогичное количество при расчете суммы целых чисел. Сравнение алгоритмов при разных n наглядно демонстрирует принципиальную разницу между ними. 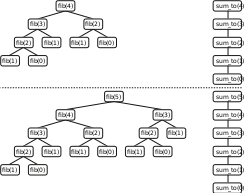 Рис. 8.1 Сравнение алгоритмов функций fib и sum_to) При увеличении аргумента, передаваемого функции sum_to, с 4 до 5 количество вызываемых функций для получения результата также возрастает с 4 до 5. Таким образом, в общем случае увеличение аргумента на единицу для этой функции ведет к вызову одной дополнительной функции при вычислении результата. Здесь наблюдается линейный рост сложности алгоритма в зависимости от величины аргумента, а количеств о рекурсивных вызовов функции прямо пропорционально величине исходного аргумента. В то же время при увеличении аргумента, передаваемого в функцию fib, с 4 до 5 количество вызовов функций возрастет с 9 до 15. Так что прирост числа n на единицу в случае с вычислением чисел Фибоначчи практически удваивает количество рекурсивных вызовов внутри функции. Такой рост сложности алгоритма называется экспоненциальным. Эффективность алгоритмов подобного типа существенно страдает при их запуске для больших значений, поскольку требует двойного прироста времени при каждом увеличении значения аргумента на единицу. 8.3. подсчет символовРекурсивные алгоритмы применимы в большом количестве задач, определения которых могут быть выражены через самих себя. И список подобных задач не ограничивается работой с целыми числами. Представьте, что вам необходимо выяснить, сколько раз определенный символ встречается в строке. Для решения этой задачи может быть написана рекурсивная функция, принимающая на вход строку и искомый символ и возвращающая количество появлений этого символа в строке. Базовый случай для этой функции возникает, если переданная в нее строка является пустой. Логично предположить, что число вхождений любого символа в пустую строку равно нулю, и именно такой результат возвращается из функции – без дополнительных рекурсивных вызовов. Если в функцию передана непустая строка, количество вхождений в нее определенного символа можно определить при помощи следующего рекурсивного алгоритма. Для упрощения определения рекурсивного случая выделим часть переменной s с исходной строкой, но без первой буквы. Таким образом, подобной урезанной частью строки, состоящей из единственного символа, будет пустая строка. Если первым символом в строке s будет искомый символ из переменной ch, то количество его вхождений в строку будет равно единице плюс количество вхождений этого символа в урезанную строку (без первой буквы). В противном случае число вхождений ch в строку s будет равно просто числу его вхождений в урезанную строку. Это определение будет постепенно стремиться к базовому случаю рекурсии (когда строка s окажется пустой), поскольку сокращенная строка всегда короче полной. Программа, в которой реализован данный алгоритм, представлена ниже. # Посчитать, сколько раз символ входит в строку # @param s – строка, в которой мы будем искать вхождения # @param ch – искомый символ # @return количество вхождений символа ch в строку s def count(s, ch): if s == "": return 0 # Базовый случай # Сокращаем строку, отсекая первый символ tail = s[1 : len(s)] # Рекурсивные случаи if ch == s[0]: return 1 + count(tail, ch) else: return count(tail, ch) # Считаем количество вхождений символа в строку s = input("Введите строку: ") ch = input("Введите искомый символ: ") print("'%s' появляется %d раз в строке '%s'" % (ch, count(s, ch), s)) |
