решение 221-задания. Сборник задач по общей физике И. Е. Иродов, И. В. Савельев, О. И. Замшагод издания 1975
 Скачать 41.1 Kb. Скачать 41.1 Kb.
|
|
(сборник задач по общей физике И.Е.Иродов, И.В.Савельев, О.И. Замша-год издания 1975) Релятивистская механика 1.181. Стержень движется в продольном направлении с постоянной скоростью ʋ относительно инерциальной К-системы отсчёта. При каком значении ʋ длина стержня в этой системе отсчёта будет на ƞ=0,5% меньше его собственной длины. (ответ: ʋ=с 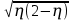 =0,1с, где с-скорость света) =0,1с, где с-скорость света)Дано L=L0 – n L0 n = 0,005 Найти v - ? Решение Релятивистское (Лоренцово) сокращение длины стержня описывается уравнением L = L0 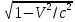 где L0– длина стержня в системе координат K,относительно которой стержень покоится (собственная длина); L– длина стержня в системе координат К`, относительно которой он движется со скоростью V вдоль оси XX'. Стержень параллелен оси XX'. где L0– длина стержня в системе координат K,относительно которой стержень покоится (собственная длина); L– длина стержня в системе координат К`, относительно которой он движется со скоростью V вдоль оси XX'. Стержень параллелен оси XX'.следовательно можно записать его с учетом условия задачи L=L0(1 – n) L0(1 – n)= L0 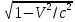 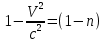 2 2V2 = (1 - 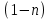 2)c2 2)c2V = c 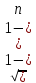 = c = c 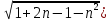 = c = c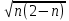 V = 3*108* 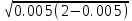 = 0.1*3*108 = 0.3*108 (м/с) = 0.1*3*108 = 0.3*108 (м/с)Ответ V = 0,1 c, V = 0.3*108 м/с 1.188. В двух точках К-системы отсчёта произошли события, разделённые промежутком времени Δt. Показать, что если эти события причинно связаны в К-системе (например, выстрел и попадание пули в мишень), то они причинно связаны и в любой другой инерциальной К'-системе отсчёта. (ответ: для этого необходимо убедиться в том, что если Δt=t2-t1>0, то и Δt'=t2'-t1'>0) Рассмотрим события А(t,x,y,z) и Б(Δt,x+а,y,z) А (0,0,0,0) Б(Δt,a,0,0) для них справедливо Δt 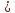 |a|/c |a|/cесли взять эти же события в другой системе, то учитывая, что пространственные координаты любой точки и соответствующий им момент времени в системах К и К' связаны преобразованиями Лоренца: 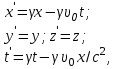 А (0,0,0,0) и Б(γ ( Δt – aV/c2) ,γ(a – ΔtV),0,0) где γ– Лоренц-фактор, определяемый выражением 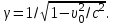 теперь( Δt`)2 - (a`/c)2 = γ2 ( Δt – aV/c2)2 - γ2 (a – ΔtV)2/с2 = γ2 (( Δt – aV/c2)2 - (a – ΔtV)2/с2 )= Δt2 – a2/c2 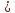 0 следовательно Δt` 0 следовательно Δt` 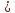 a`/c a`/cчто и требовалось доказать. можно еще так , как ниже пишут..))) что то же самое)  1.197. В плоскости xy К-системы отсчёта движется частица, проекции скорости которой равны ʋx и ʋy. Найти скорость ʋ' этой частицы в К'-системе, которая перемещается со скоростью V относительно К-системы в положительном направлении её оси x. ответ: ʋ'= 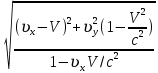 как мне кажется правильный ответ 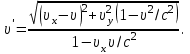 известны следствия вытекающие из преобразований Лоренца так называемый закон сложения скоростей v`x =( vx + v)/( 1+ vxv/c2) v`y= vy 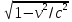 /(1+ vxv/c2) /(1+ vxv/c2) в нашем случае v`x =( vx - v)/( 1- vxv/c2) v`y= vy 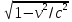 /(1- vxv/c2) /(1- vxv/c2) следовательно v` = 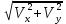 = = 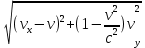 / (1 - / (1 - 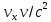 ) )1.225. Энергия фотона в К-системе равна 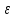 . Воспользовавшись формулами преобразования, приведёнными в предыдущей задаче, найти энергию . Воспользовавшись формулами преобразования, приведёнными в предыдущей задаче, найти энергию 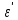 этого фотона в К'-системе, перемещающейся со скоростью V относительно К-системы в направлении движения фотона. При каком значении V энергия фотона этого фотона в К'-системе, перемещающейся со скоростью V относительно К-системы в направлении движения фотона. При каком значении V энергия фотона 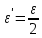 . .(ответ: 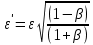 , где , где 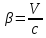 V= V=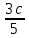 ) )Формулы из предыдущей задачи 1.224: 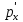 = =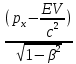 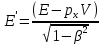 , где , где 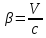 Примем, что ε = с рх ру = рz = 0 известно, что Связь между полной энергией и импульсом релятивистской частицы, измеренными в системах К и К': 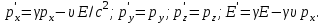 где γ– Лоренц-фактор, определяемый выражением 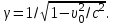 , тогда , тогда ε` = (ε – v ε/c) / 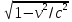 , учитывая, что ε` =ε/2 , учитывая, что ε` =ε/2ε/2 = (ε – v ε/c) / 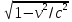 ½ = (1– v /c) / 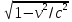 ½ = 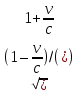 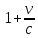 = = 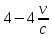 5 v /c = 3 v = 3c/5 |
