практическая 11. Сечения, развертки многогранников. Вычисление объемов
 Скачать 23.76 Kb. Скачать 23.76 Kb.
|
|
Практические занятия № 11 по теме: «Сечения, развертки многогранников. Вычисление объемов» Карточка 1 1. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой 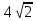 см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45 ˚. Найти площадь боковой поверхности этой пирамиды. см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45 ˚. Найти площадь боковой поверхности этой пирамиды.2. Основание прямой призмы - прямоугольный треугольник с катетами 5 см и 12 см. Вычислить площадь боковой и полной поверхности призмы, если её наибольшая боковая грань – квадрат. Карточка 2 1. Высота правильной четырёхугольной пирамиды равна 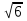 см, а боковое ребро наклонено к плоскости основания под углом 60˚. Найти площадь боковой поверхности этой пирамиды. см, а боковое ребро наклонено к плоскости основания под углом 60˚. Найти площадь боковой поверхности этой пирамиды.2. Основание прямого параллелепипеда - ромб с большей диагональю 8 см. Меньшая диагональ параллелепипеда равна 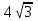 см и образует с боковым ребром угол 60˚. Вычислить площадь боковой поверхности этого параллелепипеда. см и образует с боковым ребром угол 60˚. Вычислить площадь боковой поверхности этого параллелепипеда.Карточка 3 1. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой 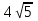 см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 30 ˚. Найти площадь боковой поверхности этой пирамиды. см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 30 ˚. Найти площадь боковой поверхности этой пирамиды.2. Основание прямой призмы - прямоугольный треугольник с катетами 5 см и 12 см. Вычислить площадь боковой и полной поверхности призмы, если её наименьшая боковая грань – квадрат. Карточка 4 1. Высота правильной четырёхугольной пирамиды равна 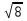 см, а боковое ребро наклонено к плоскости основания под углом 45˚. Найти площадь боковой поверхности этой пирамиды. см, а боковое ребро наклонено к плоскости основания под углом 45˚. Найти площадь боковой поверхности этой пирамиды.2. Основание прямого параллелепипеда - ромб с большей диагональю 16 см. Меньшая диагональ параллелепипеда равна 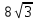 см и образует с боковым ребром угол 30˚. Вычислить площадь боковой поверхности этого параллелепипеда. см и образует с боковым ребром угол 30˚. Вычислить площадь боковой поверхности этого параллелепипеда. |
