сем 8 Магнитное поле, теорема о цирк. теория, формулы,. Семинар 8 Магнитное поле Закон БиоСавараЛапласа Закон БиоСавараЛапласа Сила Ампера
 Скачать 1 Mb. Скачать 1 Mb.
|
Семинар 8 Магнитное поле
Теорема о циркуляции Т  еорема Гаусса для вектора магнитной индукции еорема Гаусса для вектора магнитной индукцииДля наглядного графического представления магнитного поля, как и в случае электростатического поля, используют линии магнитной индукции: Касательная к ним ||  ; Густота линий ; Густота линий  П  опробуем изобразить линии магнитной индукции для прямого тока. опробуем изобразить линии магнитной индукции для прямого тока.Замечание: Правило буравчика можно применить и здесь: куда нужно крутить буравчик, чтобы его поступательное движение совпадало с направлением тока? Туда и направлены линии магнитной индукции. Свойства линий магнитной индукции: Всегда замкнуты (не имеют начала и конца) Любая линия, входящая в замкнутую поверхность, выходит из неё. Математически эти свойства записываются следующим образом:  – Теорема Гаусса для вектора магнитной индукции. – Теорема Гаусса для вектора магнитной индукции.Физический смысл: В природе отсутствуют магнитные заряды. Теорема о циркуляции вектора магнитной индукции Вычислим циркуляцию вектора магнитной индукции для уже рассмотренного прямого тока (см. рисунок). В качестве контура интегрирования выберем окружность радиуса R с центром на проводнике. Фактически будем интегрировать вдоль силовой линии магнитной индукции: 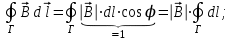    Можно показать, что это выражение справедливо всегда, а не только для прямого тока.  – Теорема о циркуляции вектора магнитной индукции – Теорема о циркуляции вектора магнитной индукцииГО-11.2: Задача решена в учебнике Иродова: пример 1, §6.4. К  оаксиальный кабель состоит из внутреннего сплошного цилиндрического проводника радиуса R и наружной тонкостенной проводящей трубки радиуса 3R. Найти индукцию магнитного поля в зависимости от расстояния r до оси кабеля, если по внутреннему проводнику и по проводящей трубке текут токи одинаковой величины I a) в одном направлении, б) в противоположных направлениях. Tоки I равномерно распределены по сечению внутреннего проводника и по поверхности проводящей трубки. Магнитная проницаемость всюду равна 1. оаксиальный кабель состоит из внутреннего сплошного цилиндрического проводника радиуса R и наружной тонкостенной проводящей трубки радиуса 3R. Найти индукцию магнитного поля в зависимости от расстояния r до оси кабеля, если по внутреннему проводнику и по проводящей трубке текут токи одинаковой величины I a) в одном направлении, б) в противоположных направлениях. Tоки I равномерно распределены по сечению внутреннего проводника и по поверхности проводящей трубки. Магнитная проницаемость всюду равна 1.Решение: Из симметрии задачи следуют 2 факта: Линии вектора магнитной индукции имеют вид окружностей с центром на оси провода. Модуль вектора  одинаков во всех точках, находящихся на одинаковом расстоянии от оси. одинаков во всех точках, находящихся на одинаковом расстоянии от оси.Теорема о циркуляции магнитной индукции:  ; ;Контур интегрирования – окружность радиуса r. Левая часть уравнения приводит к одному и тому же результату, независимо от радиуса r:  ; ;Правая часть в разных областях даёт разный результат: 1)   , где , где  – совпадает с формулой прямого тока. – совпадает с формулой прямого тока.   2)    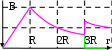   3)  а)     б)   Поле бесконечного соленоида. Иродов Пример 2 §6.4 С  оленоид – катушка с током. Поле внутри него складывается из полей, создаваемых отдельными витками. Будем считать длину соленоида бесконечной. В этом случае можно считать, что линии магнитной индукции замыкаются на бесконечности и вне соленоида поля не будет. Запишем теорему о циркуляции магнитной индукции для контура, изображённого на рисунке: оленоид – катушка с током. Поле внутри него складывается из полей, создаваемых отдельными витками. Будем считать длину соленоида бесконечной. В этом случае можно считать, что линии магнитной индукции замыкаются на бесконечности и вне соленоида поля не будет. Запишем теорему о циркуляции магнитной индукции для контура, изображённого на рисунке:   только на нижнем отрезке контура. Значит: только на нижнем отрезке контура. Значит:   – поле соленоида. – поле соленоида.Сила Ампера На элемент тока  в магнитном поле в магнитном поле  действует сила Ампера: действует сила Ампера:  Сила взаимодействия параллельных токов П  рямой провод рямой провод 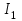 создаёт на проводнике магнитное поле создаёт на проводнике магнитное поле  . .Подставим в выражение для силы Ампера и учтём, что  (т.е. (т.е.  ): ): Направление действия силы зависит от взаимной ориентации токов (см. рис.). В задачах часто используют силу в расчете на единицу длины проводников:   Замечания: Рассмотрение тока 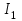 в поле проводника в поле проводника 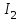 даёт тот же результат. Ср. с законом Кулона. даёт тот же результат. Ср. с законом Кулона.Это именно сила взаимодействия двух бесконечных токов в расчете на единицу длины, а не сила взаимодействия двух проводов единичной длины. Почувствуйте разницу! И-2.274 Д  ва параллельных длинных провода с током I=6 А в каждом (токи направлены в одну сторону) удалили друг от друга так, что расстояние между ними стало в η=2 раза больше первоначального. Какую работу на единицу длины проводов совершили при этом силы Ампера? ва параллельных длинных провода с током I=6 А в каждом (токи направлены в одну сторону) удалили друг от друга так, что расстояние между ними стало в η=2 раза больше первоначального. Какую работу на единицу длины проводов совершили при этом силы Ампера?Решение: Пусть начальное расстояние между проводами b. Тогда конечное расстояние: ηb. Найдём элементарную работу при удалении проводов. Токи сонаправлены, они притягиваются. Вектора силы и перемещения направлены в разные стороны и элементарная работа отрицательна:   ГО–12-11 (И–2.278) П  о двум длинным тонким параллельным проводникам, вид которых показан на рисунке, текут постоянные токи I1 и I2. Расстояние между проводниками a, ширина правого проводника b. Имея в виду, что оба проводника лежат в одной плоскости, найдите величину F силы магнитного взаимодействия проводников в расчёте на единицу их длины. о двум длинным тонким параллельным проводникам, вид которых показан на рисунке, текут постоянные токи I1 и I2. Расстояние между проводниками a, ширина правого проводника b. Имея в виду, что оба проводника лежат в одной плоскости, найдите величину F силы магнитного взаимодействия проводников в расчёте на единицу их длины.Решение: Разобьём правый проводник на элементарные проводники толщины dx. По каждому из них протекает ток  Элементарная сила, действующая на его единицу длины:  Просуммируем эти силы:   Электромагнитная индукция Правило буравчика (правого винта)  Магнитный поток через контур с током М  агнитный поток: агнитный поток: 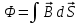 ; [Ф]=1 Вб (Вебер). ; [Ф]=1 Вб (Вебер).Рассмотрим плоский контур с током в однородном магнитном поле. Выберем систему координат так, что ось Z перпендикулярна плоскости контура. Тогда:   Положительное направление тока выбираем так, чтобы оно составляло правый винт с нормалью. Закон электромагнитной индукции В замкнутом проводящем контуре при изменении охватываемого им магнитного потока возникает электрический ток  Продемонстрировать, как определить направление индукционного тока с помощью этой формулы. На самом же деле для этого удобнее использовать правило Ленца: «  Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей» Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей»В формуле закона электромагнитной индукции правилу Ленца соответствует знак «минус». Разобрать определение направления индукционного тока в контуре при приближении к нему соленоида (рис). ГО–13.1 Н  еподвижный П-образный проводник с пренебрежимо малым сопротивлением находится в постоянном однородном магнитном поле, вектор индукции еподвижный П-образный проводник с пренебрежимо малым сопротивлением находится в постоянном однородном магнитном поле, вектор индукции  которого составляет угол с плоскостью проводника. По проводнику без нарушения контакта скользит с постоянной скоростью V перемычка CD. Сопротивление перемычки R, длина a. Укажите направление индукционного тока I и найдите его величину. которого составляет угол с плоскостью проводника. По проводнику без нарушения контакта скользит с постоянной скоростью V перемычка CD. Сопротивление перемычки R, длина a. Укажите направление индукционного тока I и найдите его величину.Решение: По правилу Ленца индукционный ток направлен так, что его магнитное поле противодействует изменению магнитного потока. При таком движении перемычки поток увеличивается, т.к. площадь контура растет, т.о. индукционное магнитное поле должно уменьшать магнитный поток. Искомое направление тока см. на рисунке.      ГО–13.5 (И-2.317) Д  линный прямой проводник с током I и П-образный проводник с подвижной перемычкой расположены в одной плоскости (см. рис.). Перемычку, длина которой l, перемещают вправо с постоянной скоростью V, перепендикулярной стержню. Найдите ЭДС индукции в контуре как функцию расстояния r. линный прямой проводник с током I и П-образный проводник с подвижной перемычкой расположены в одной плоскости (см. рис.). Перемычку, длина которой l, перемещают вправо с постоянной скоростью V, перепендикулярной стержню. Найдите ЭДС индукции в контуре как функцию расстояния r.Решение:  Найдём изменение потока за время dt. Найдём изменение потока за время dt.Магнитная индукция, создаваемая током I, перпендикулярна рамке:  . .В пределах площади dS можно считать     – поле прямого тока. Подставим: – поле прямого тока. Подставим:   ГО–13.6 (И-2.318) К  вадратная рамка со стороной a и длинный прямой провод с током I находятся в одной плоскости (см. рисунок). Рамку поступательно перемещают вправо с постоянной скоростью V. Найти ЭДС индукции в рамке как функцию расстояния x. вадратная рамка со стороной a и длинный прямой провод с током I находятся в одной плоскости (см. рисунок). Рамку поступательно перемещают вправо с постоянной скоростью V. Найти ЭДС индукции в рамке как функцию расстояния x.Решение:  Аналогично предыдущей задаче найдём изменение потока за время dt. Поток увеличится на величину dΦ1 и уменьшится на dΦ2: Аналогично предыдущей задаче найдём изменение потока за время dt. Поток увеличится на величину dΦ1 и уменьшится на dΦ2:  . .    Комментарий: Магнитное поле рядом с проводом больше, чем на расстоянии x+a. Поэтому по мере движения рамки магнитный поток через рамку будет уменьшаться. А, значит, индукционный ток будет стараться его «поддержать». Следовательно, знак ЭДС должен быть положительным, как мы и получили. Направление индукционного тока показано на рисунке. ГО–13.18 (а) К  вадратная рамка из медной проволоки находится в однородном магнитном поле, величина индукции В которого зависит от времени. Ось Z перпендикулярна плоскости рамки. Сторона рамки а=10 см, радиус проволоки r=1 мм, удельное сопротивление меди 1,7.10-8 Ом м. Определите направление и величину индукционного тока I в момент t0=2 с, если проекция вектора вадратная рамка из медной проволоки находится в однородном магнитном поле, величина индукции В которого зависит от времени. Ось Z перпендикулярна плоскости рамки. Сторона рамки а=10 см, радиус проволоки r=1 мм, удельное сопротивление меди 1,7.10-8 Ом м. Определите направление и величину индукционного тока I в момент t0=2 с, если проекция вектора  на ось Z зависит от времени t по закону Вz=0,1t2-0,4; (Вz – в Теслах, t – в секундах). на ось Z зависит от времени t по закону Вz=0,1t2-0,4; (Вz – в Теслах, t – в секундах).Решение: После выбора нормали к контуру направление индукционного тока определяется его знаком (см. рис): Ii>0: Ii и Z образуют правый винт; Ii<0: Ii и Z образуют левый винт.        Материал для консультации ГО–10.7 (Поле прямого тока) Д  оказать, что в точке А величина индукции магнитного поля B, создаваемого прямолинейным отрезком тонкого провода с током I определяется формулой: оказать, что в точке А величина индукции магнитного поля B, создаваемого прямолинейным отрезком тонкого провода с током I определяется формулой:  , где расстояние х и углы определяют положение точки A относительно отрезка (см. рис.). , где расстояние х и углы определяют положение точки A относительно отрезка (см. рис.).Переформулируем условие задачи: «Найти индукцию магнитного поля B, создаваемого прямолинейным отрезком проводника с током I в точке А, положение которой относительно отрезка задано углами α1, α2 и расстоянием х (см. рис.)». Решение: Рассмотрим сначала отдельно вклад от верхней половины провода с током. Разобьём провод на бесконечно малые элементы тока. Для каждого из них можно записать закон Био-Савара:  . .Вклады в поле от всех элементов имеют одно и то же направление – от нас (см. рисунок). Это означает, что при интегрировании можно суммировать не вектора, а только их длины:   ; ;Интегрировать будем по углу α, поэтому все переменные величины надо выразить через этот угол и его приращение:  ; ;  В нижней части, как выясняется, будет всё то же самое: создаваемое поле направлено в ту же сторону  вместо вместо  будет будет  (рис.) (рис.) . .   Следствие: Если провод бесконечен, то  . Тогда: . Тогда:  – поле прямого тока – поле прямого токаГО–10.8 Д  ва прямолинейных длинных тонких провода расположены параллельно на расстоянии h=10 см друг от друга. По проводникам текут токи I1=I2=5 А в противоположных направлениях. Найти модуль и направление индукции ва прямолинейных длинных тонких провода расположены параллельно на расстоянии h=10 см друг от друга. По проводникам текут токи I1=I2=5 А в противоположных направлениях. Найти модуль и направление индукции  магнитного поля в точке, находящейся на расстоянии d=10 см от каждого проводника. магнитного поля в точке, находящейся на расстоянии d=10 см от каждого проводника.Решение:  . .Строим вектора  и и  : :  (закон Био-Савара). (закон Био-Савара). – поле прямого тока; – поле прямого тока;   ГО–10.11 Н  айти магнитную индукцию в центре контура, имеющего вид прямоугольника, если его диагональ d=16 см, угол между диагоналями φ=30º и ток I=5 А. айти магнитную индукцию в центре контура, имеющего вид прямоугольника, если его диагональ d=16 см, угол между диагоналями φ=30º и ток I=5 А.Решение:  . Очевидно, что все эти вклады имеют одно и то же направление. Кроме того: . Очевидно, что все эти вклады имеют одно и то же направление. Кроме того:  . .Из задачи 10.7:  Аналогично:  ; ; 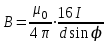 ГО–11-10 (И-2.241) Иродов – Пример 4 из §6.4. О  пределите величину В индукции магнитного поля тока, однородно распределённого: пределите величину В индукции магнитного поля тока, однородно распределённого:а) По плоскости с линейной плотностью  б) По двум параллельным плоскостям с линейными плотностями  и и  Решение: а)  – вектор, совпадающий по направлению с током, а численно равен: – вектор, совпадающий по направлению с током, а численно равен:  – ток, приходящийся на единицу длины пластины. Разбив мысленно плоскость с током на тонкие нити с током, нетрудно сообразить, что результирующий вектор магнитной индукции будет направлен параллельно пластине, как это изображено в нижней части рисунка. Применим теорему о циркуляции магнитной индукции к контуру 1-2-3-4, изображённому на рисунке: – ток, приходящийся на единицу длины пластины. Разбив мысленно плоскость с током на тонкие нити с током, нетрудно сообразить, что результирующий вектор магнитной индукции будет направлен параллельно пластине, как это изображено в нижней части рисунка. Применим теорему о циркуляции магнитной индукции к контуру 1-2-3-4, изображённому на рисунке:    и и  равны нулю, т.к. на участках 2-3 и 4-1 равны нулю, т.к. на участках 2-3 и 4-1  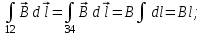    – магнитное поле плоскости с током – магнитное поле плоскости с токомб) Воспользуемся результатом, полученным в пункте (а):  Между плоскостями эти поля будут складываться:  Вне плоскостей поля пластин друг друга уничтожают:  ГО–11-11. (И-2.242) П  остоянный ток течёт внутри бесконечно протяжённой пластины толщины 2d параллельно её поверхности. Плотность тока j однородно распределена по сечению пластины. Найдите величину В индукции магнитного поля этого тока как функцию расстояния x от средней плоскости пластины. остоянный ток течёт внутри бесконечно протяжённой пластины толщины 2d параллельно её поверхности. Плотность тока j однородно распределена по сечению пластины. Найдите величину В индукции магнитного поля этого тока как функцию расстояния x от средней плоскости пластины.Решение: Направление вектора магнитной индукции определяется аналогично предыдущей задаче. Применим теорему о циркуляции магнитной индукции к контуру, показанному на рисунке:    1)   2)   ГО–13.7 К  вадратная проволочная рамка и длинный прямой провод с током I1 находятся практически в одной плоскости и электрически изолированы друг от друга (провод покрыт лаком). Сопротивление рамки R, длина её стороны a. Рамку поступательно перемещают с постоянной скоростью V, как показано на рисунке. Найдите ток I2(0) в рамке в момент времени, когда она будет симметрично расположена относительно провода. Постройте примерный график зависимости силы тока I2(x) в рамке от координаты x её центра C. вадратная проволочная рамка и длинный прямой провод с током I1 находятся практически в одной плоскости и электрически изолированы друг от друга (провод покрыт лаком). Сопротивление рамки R, длина её стороны a. Рамку поступательно перемещают с постоянной скоростью V, как показано на рисунке. Найдите ток I2(0) в рамке в момент времени, когда она будет симметрично расположена относительно провода. Постройте примерный график зависимости силы тока I2(x) в рамке от координаты x её центра C.Решение:  За время dt: За время dt: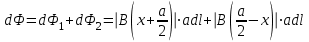     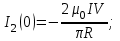  ГО–13.18 (б, в) б) Вz=0,4t(2-t);   в) Вz=0,4 sin(t);   И-2.324 Квадратная проволочная рамка со стороной a и прямой проводник с постоянным током I лежат в одной плоскости (см. рис.). Сопротивление рамки R. Её повернули на 180° вокруг оси OO', отстоящей от проводника с током на расстояние b. Найти кол-во электричества, протекшее в рамке.  Решение: Решение:   При повороте контура нормаль к нему изменяет направление на противоположное. Значит, изменит знак и поток через него (см. рис.):  Сумма этих потоков – не что иное, как поток через большой прямоугольник, составленный из двух этих квадратных контуров:    Замечание: При решении мы не учитывали индуктивность контура, т.е. не принимали во внимание явление самоиндукции. Оказывается, этого и не надо делать: в начальном и конечном состояниях ток через контур не протекает. Значит, весь заряд, протекший в контуре за счёт самоиндукции при увеличении тока, вернулся обратно при его уменьшении. Т.о. самоиндукция не скажется на результате расчёта. ГО–13.14 К  вадратную рамку из N=200 витков равномерно вращают в однородном магнитном поле В=0,015 Тл вокруг оси, лежащей в плоскости рамки и перпендикулярной полю. Площадь каждого витка S=300 см2. Определите ЭДС индукции E(t) через время t=0,01 с после начала движения рамки из положения, когда ее плоскость была перпендикулярна вектору вадратную рамку из N=200 витков равномерно вращают в однородном магнитном поле В=0,015 Тл вокруг оси, лежащей в плоскости рамки и перпендикулярной полю. Площадь каждого витка S=300 см2. Определите ЭДС индукции E(t) через время t=0,01 с после начала движения рамки из положения, когда ее плоскость была перпендикулярна вектору  , если амплитуда ЭДС Em=7,2 B. , если амплитуда ЭДС Em=7,2 B.Решение:   где Bn – проекция магнитной индукции на нормаль к рамке. где Bn – проекция магнитной индукции на нормаль к рамке.  . Через время t рамка повернётся на угол . Через время t рамка повернётся на угол  . .  Неизвестную частоту легко определить из амплитуды ЭДС:   Семинар 8. Магнитное поле. Справочный материал для студентов Закон Био-Савара-Лапласа Закон Био-Савара-Лапласа:  Сила Ампера: Сила Ампера:  Поле движущегося заряда:  Сила Лоренца: Сила Лоренца:  Поле прямого тока:  Поле кругового тока:  ; Поле дуги: ; Поле дуги:  Теорема о циркуляции вектора магнитной индукции Теорема Гаусса для вектора магнитной индукции:  Теорема о циркуляции вектора магнитной индукции:  Сила Ампера Сила Ампера:  Сила, действующая на прямолинейный проводник в однородном магнитном поле:  Сила взаимодействия параллельных токов в расчете на единицу длины:  Закон электромагнитной индукции Магнитный поток: 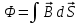 Закон электромагнитной индукции: «В замкнутом проводящем контуре при изменении охватываемого им магнитного потока возникает электрический ток  ». ».Правило Ленца: «Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей» Контрольная работа №7а 1. Найти ёмкость цилиндрического конденсатора длины l, радиусы обкладок которого a и b, причем a  , где β=const. , где β=const.2. Найти ёмкость сферического конденсатора, радиусы обкладок которого a и b, причем a<b, если пространство между обкладками заполнено диэлектриком, проницаемость которого зависит от расстояния r до центра конденсатора как  , где β=const. , где β=const.3. Найти ёмкость сферического конденсатора, радиусы обкладок которого a и b, причем a<b, если пространство между обкладками заполнено диэлектриком, проницаемость которого зависит от расстояния r до центра конденсатора как  , где β=const. , где β=const.4. Найти ёмкость цилиндрического конденсатора длины l, радиусы обкладок которого a и b, причем a<b, если пространство между его обкладками заполнено диэлектриком, проницаемость которого зависит от расстояния r до оси конденсатора как  , где β=const. , где β=const.5. Четыре одинаковых точечных заряда q расположены в вершинах квадрата со стороной a. Какую работу совершают силы электрического поля при перемещении зарядов в вершины тетраэдра со стороной a? 6. На оси x в точках с координатами 0, a и 2a расположены точечные заряды q, (–2q) и 3q. Какую работу нужно совершить, чтобы поменять заряды q и (–2q) местами? 7. Четыре одинаковых точечных заряда q расположены на одной прямой. Расстояние между соседними зарядами равно a. Какую работу нужно совершить, чтобы переместить их в вершины квадрата со стороной a? 8. На оси x в точках с координатами 0, a и 2a закреплены точечные заряды q, 2q и q. Крайние заряды освобождают. Найти их максимальные скорости, если масса каждого заряда m. 9. Величины E, r, I1 известны. Найти I2 (рис.).  10. Величины E, r, I1 известны. Найти I2 (рис.).  11. Величины E, r, I1 известны. Найти I2 (рис.).  12. Величины E, r, I1 известны. Найти I2 (рис.).  Контрольная работа №7б
16. Коаксиальный кабель состоит из внутреннего сплошного цилиндрического проводника радиуса 2R и наружной тонкостенной проводящей трубки радиуса 4R. Найти индукцию магнитного поля в точках, удалённых от оси цилиндров на расстояние R, если по внутреннему проводнику и по проводящей трубке текут токи одинаковой величины I в одном направлении. Ток равномерно распределён по сечению внутреннего проводника и по поверхности проводящей трубки. Магнитная проницаемость всюду равна 1. 17. Коаксиальный кабель состоит из внутреннего сплошного цилиндрического проводника радиуса 2R и наружного цилиндрического слоя с внутренним радиусом 3R и внешним радиусом 5R. Найти индукцию магнитного поля в точках, удалённых от оси на расстояние 4R, если по внутреннему проводнику и по проводящей трубке текут токи одинаковой величины I в одном направлении. Ток равномерно распределён по сечению проводников. Магнитная проницаемость всюду равна 1. 18. Коаксиальный кабель состоит из внутреннего сплошного цилиндрического проводника радиуса 2R и наружного цилиндрического слоя с внутренним радиусом 3R и внешним радиусом 5R. Найти индукцию магнитного поля в точках, удалённых от оси на расстояние 4R, если по внутреннему проводнику и по проводящей трубке текут токи одинаковой величины I в разных направлениях. Ток равномерно распределён по сечению проводников. Магнитная проницаемость всюду равна 1. 19. Два прямолинейных длинных параллельных проводника находятся на расстоянии a = 10 см друг от друга. По проводникам в одном направлении текут токи I1 = 20 А и I2 = 30 А. Какую работу A надо совершить (на единицу длины проводников), чтобы раздвинуть эти проводники до расстояния b = 20 см? 20. Два прямолинейных длинных параллельных проводника находятся на некотором расстоянии друг от друга. По проводникам текут одинаковые токи в одном направлении. Найти токи, текущие по каждому из проводников, если известно, что для того, чтобы увеличить в 2 раза расстояние между проводниками, пришлось совершить работу (на единицу длины проводников) A = 55 мкДж/м. 21. Квадратная рамка с сопротивлением R и стороной a находится в однородном магнитном поле, величина индукции которого зависит от времени по закону B(t)=At2+D, где A и D – постоянные. Вектор магнитной индукции составляет постоянный угол α с нормалью к плоскости рамки. Определить зависимость индукционного тока в рамке от времениI(t). 22. Квадратная рамка с сопротивлением R и стороной a находится в однородном магнитном поле, величина индукции которого зависит от времени по закону B(t)=Ae–βt, где A и β – постоянные. Вектор магнитной индукции составляет постоянный угол α с нормалью к плоскости рамки. Определить зависимость индукционного тока в рамке от времени I(t). 8– |

 о круговому витку радиуса R=100 см из тонкого провода циркулирует ток I=1 А. Найти магнитную индукцию в центре витка.
о круговому витку радиуса R=100 см из тонкого провода циркулирует ток I=1 А. Найти магнитную индукцию в центре витка. . Просуммируем:
. Просуммируем: 
 – поле кругового тока.
– поле кругового тока. ледствие: Полученную формулу можно обобщить на случай, когда провод образует не кольцо, а дугу. В этом случае вместо длины окружности нужно взять длину дуги:
ледствие: Полученную формулу можно обобщить на случай, когда провод образует не кольцо, а дугу. В этом случае вместо длины окружности нужно взять длину дуги: 
 – магнитное поле дуги.
– магнитное поле дуги.

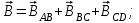




 – половина поля прямого тока
– половина поля прямого тока



 – половина прямого тока
– половина прямого тока