Сфера, вписанная в многогранник
 Скачать 172 Kb. Скачать 172 Kb.
|
|
Тема проекта: Комбинация многогранников и фигур вращения. Тема урока: «Сфера, вписанная в многогранник». Тип урока: школьная лекция. Количество академических часов: 2. Учебник: «Геометрия 10-11» авторов Л.С. Атанасян и др. (11-й класс) Разработчики: Родионова Н., Виноградова Л. Учебная задача: рассмотреть вместе с учащимися основные комбинации многогранников с вписанной сферой: установить (т.е. «открыть») основные теоретические факты, применить их к решению задач, тем самым, формируя логические и графические умения школьников; убедить учащихся в необходимости изучения темы. Диагностируемые цели: В результате ученик: знает – основные теоретические положения темы: теоремы о том, когда в призму и пирамиду можно вписать сферу и схему построения центра сферы, вписанной в пирамиду, у которой все боковые грани равнонаклонены к плоскости основания; – основные ключевые задачи и умеет ими пользоваться; умеет – производить наглядный чертеж к задаче, оптимально полезный в данном случае; – решать задачи на различные комбинации многогранников с вписанной сферой; осознает – практическое применение данной темы и необходимость её изучения; – эстетичность и гармоничность изображений комбинаций многогранников с вписанной сферой. Оборудование урока: мел, проектор, доска, экран для отображения информации, презентация. Ход работы 1-й урок. 1. Актуализация: повторение фактов, касающихся вписанной окружности. 2. Мотивация: от вписанной окружности учитель переходит по аналогии к вписанной сфере, сообщает эпиграф к уроку, рассказывает о практическом применении вписанной сферы. 3. Постановка учебных задач: формулировка темы и цели урока. 4. В совместной деятельности с учащимися, используя модели или рисунки сферы, вписанной в пирамиду и прямую призму, выясняются условия, при которых в призму и пирамиду можно вписать сферу. После того, как будут сформулированы теоремы, учащимся раздаются листы, на которых эти теоремы уже записаны. Впоследствии ученики должны вклеить их себе на обложку тетради. 5. Решение задачи 1 (см. содержательный этап). 6. Решение задачи 2 (см. содержательный этап). В ходе решения данной задачи учитель в совместной деятельности с учащимися выделяет схему построения центра сферы, вписанной в пирамиду, у которой все боковые грани равнонаклонены к плоскости основания. 7. Итоги урока, выдача домашнего задания: - приклеить лист с теоремами на обложку тетради; - выучить теоремы и схему построения центра сферы, вписанной в пирамиду, у которой все боковые грани равнонаклонены к плоскости основания; - решить две задачи (легкие – на применение теорем). 2-й урок. 1. В качестве актуализации в начале урока для небольшого повторения теорем и дополнительной мотивации при фронтальной или индивидуальной работе по карточкам выполняются задания типа «верно ли утверждение?» 2. Решение задач №3, №4. 3. Подведение итогов урока в виде кроссворда. 4. Выдача домашнего задания: - подготовиться к самостоятельной работе; - № 635, № 632, № 634. Конспект урока Ι урок (45 мин.) Мотивационно – ориентировочный этап (15мин.) а) актуализация (7 мин.) Начинается урок. Включен проектор, на экране отображается 1-й слайд презентации. На доске заранее заготовлены рисунки: 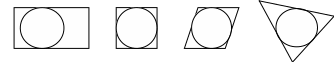 Они позволяют учащимся лучше ориентироваться при ответах на вопросы учителя. П. приветствует класс: «здравствуйте, ребята, садитесь. Начнем урок со следующего задания: обратите внимание на экран». П. просит одного из У. прочитать текст, изложенный на 1-м слайде: {Утверждение. Если в параллелограмм можно вписать окружность, то этот параллелограмм – прямоугольник.} П.: верно ли это утверждение? У.: нет. {У. скорее всего будут указывать на первый рисунок} П.: приведите пример параллелограмма, в который можно вписать окружность, но который не является прямоугольником. У.: ромб, т.к. ромб является параллелограммом и не является прямоугольником, но в него можно вписать окружность. П.: почему Вы считаете, что в ромб можно вписать окружность? У.: в ромб можно вписать окружность потому, что суммы его противоположных сторон равны. П.: верно, мы вспомнили, что для того, чтобы в параллелограмм можно было вписать окружность необходимо и достаточно, чтобы суммы противоположных сторон параллелограмма были равны. Назовите эквивалентную формулировку. У.: для того, чтобы в параллелограмм можно было вписать окружность необходимо и достаточно, чтобы этот параллелограмм являлся ромбом. П.: а можно ли вписать окружность в произвольный квадрат? У.: да, т.к. если четырехугольник является квадратом, то он является и ромбом, а, значит, в него можно вписать окружность. П.: давайте занесем эти данные в таблицу. {см. 2-ой слайд, ученики не записывают} П.: давайте рассмотрим более общий случай. Скажите, можно ли обобщить утверждение для параллелограмма на произвольный выпуклый четырехугольник? У.: да. П.: таким образом, получаем: для того, чтобы в выпуклый четырехугольник можно было вписать окружность необходимо и достаточно, чтобы суммы противоположных сторон этого четырехугольника были равны. {появляется второй пункт во 2-м слайде} П.: а как найти центр вписанной в п-угольник окружности? У.: следует найти точку пересечения биссектрис углов п-угольника. П.: верно. Но если мы знаем, что в данный п-угольник можно вписать окружность (выполняется критерий равенства сумм противоположных сторон), то достаточно найти точку пересечения биссектрис двух любых углов. {появляется 3-й слайд} П.: В какой треугольник можно вписать окружность? У.: в любой. П.: тогда, для того, чтобы найти центр вписанной в треугольник окружности, достаточно определить место положения точки пересечения биссектрис двух любых углов треугольника. {появляется 4-й слайд} П.: посмотрите на рисунок. Чем является отрезок [OH] перпендикуляра, опущенного из центра окружности к стороне АС треугольника АВС? У.: радиусом. П.: значит, для того, чтобы изобразить радиус целесообразно опустить перпендикуляр из центра окружности к любой стороне треугольника. б) мотивация (6 мин.) П.: как в этом году, так и в прошлом, мы изучаем стереометрию, до этого мы занимались планиметрией и уже неоднократно замечали, что многие понятия и теоремы стереометрии аналогичны некоторым понятиям, теоремам планиметрии. Так, мы изучали симметрию в пространстве по-аналогии с симметрией на плоскости, правильные многогранники – по-аналогии с правильными многоугольниками. Аналогом прямой в пространстве является плоскость, плоскости - пространство и т.д. Сегодня мы вспомнили ряд очень важных фактов, касающихся вписанной окружности. Как Вы думаете, существует ли пространственный аналог окружности? У.: сфера. П.: а пространственный аналог вписанной окружности? У.: вписанная сфера. П.: эпиграфом к сегодняшнему уроку будут слова Н.И. Лобачевского: «Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира». {появляется 5-й слайд} Как Вы думаете, почему выбран именно такой эпиграф? У.: потому, что, наверное, даже вписанная сфера имеет свое применение. П.: совершенно верно и сейчас мы узнаем какое именно. {появляются 6,7,8,9,10-й слайды, учитель рассказывает, опираясь на текст презентации. Здесь текст слайдов имеет второстепенное значение, он представлен в основном для учителя, поэтому тот факт, что слайды не наглядны не влияет на качество обучения} в) постановка учебных задач (2 мин.) П.: предположите, куда сфера может быть вписана? У.: в призму, пирамиду, конус, цилиндр, …. {появляется 11-й слайд. Здесь учитель должен обратить внимание учеников на то, что сфера может быть вписана не только в прямую призму, прямой конус и т.д., а может быть вписана и в наклонную призму, конус и т.д., несмотря на представленные в презентации рисунки} П.: т.е. в тела вращения и многогранники. Целесообразно рассматривать отдельно комбинации многогранников с вписанной сферой и комбинации тел вращения с вписанной сферой. Сегодня на уроке займемся рассмотрением комбинаций первого вида. Сформулируйте тему урока. {У. формулируют, П. корректирует} У.: тема урока: «Сфера, вписанная в многогранник». {появляется 12-й слайд, ученики открывают тетради, записывают тему урока} П.: мы вспомнили, что не в любой многоугольник можно вписать окружность. Примените метод аналогии и спрогнозируйте: в любой ли многогранник можно вписать сферу? У.: наверное, нет, должны выполняться определенные условия. П.: а какие? {У. затрудняются ответить} П.: какова наша задача сегодня? У.: выяснить условия, при которых в многогранник можно вписать сферу. {Появляются последние строки в 12-м слайде} 2. Содержательный и рефлексивно-оценочный этапы (30мин) В совместной деятельности с учащимися, используя модели или рисунки сферы, вписанной в пирамиду и прямую призму, выясняются условия, при которых в призму(13-й слайд) и пирамиду можно вписать сферу.(6 мин) П.: Давайте рассмотрим многоугольник, в который вписана окружность. Что является аналогом многоугольника в пространстве? У.: Многогранник. П.: А что является аналогом окружности? У.: Сфера. П.: Давайте вспомним определение вписанной в многоугольник окружности и попытаемся, по-аналогии, сформулировать определение вписанной в многогранник сферы. У.: Определение вписанной в многоугольник окружности: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник. {Далее У. конструируют определение вписанной в многогранник сферы, П. корректирует. Полученное определение У. записывают в тетради: сфера называется вписанной в многогранник, если она касается всех граней многогранника. Также обговаривается, что сфера касается грани многогранника, если плоскость грани является касательной к сфере и точка касания принадлежит грани} П.: Пусть нам даны многоугольник и вписанная в него окружность. Давайте нашим плоскостным фигурам «придадим» объем, при этом в качестве многогранника рассмотрим прямую призму. Получим сферу, вписанную в призму. Как вы думаете, при каких условиях мы сможем вписать в прямую призму сферу? У.: Когда в основание можно вписать окружность. П.: Будет ли это достаточным условием? А что вы можете сказать относительно высоты призмы? У.: Высота призмы должна быть равна диаметру вписанной сферы. П.: Итак, теперь попытайтесь сформулировать теорему о том, при каких условиях в прямую призму можно вписать сферу. {У. формулируют, П. корректирует. Появляется 14-й слайд и в нем начинает заполняться таблица} П.: Теперь попробуем выяснить, условия необходимые для того, чтобы в пирамиду можно было вписать сферу. Нам известно, что на плоскости центр вписанной в многоугольник окружности является …? У.: Точкой пересечения биссектрис углов многоугольника. П.: А что является аналогом линейного угла в пространстве? У.: Двугранный угол. П.: А что является аналогом биссектрисы в пространстве? У.: Биссектор двугранного угла. П.: Попробуйте предположить, какой вывод можно сделать, исходя из вышесказанного. У.: Центр вписанной в пирамиду сферы является точкой пересечения биссекторов всех двугранных пирамиды. П.: Совершенно верно. В общем случае это именно так. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Причем он расположен только внутри многогранника. В случае с пирамидой верна следующая теорема: «В выпуклую пирамиду можно вписать сферу тогда и только тогда, когда биссекторы всех двугранных углов при боковых ребрах пересекаются по некоторому лучу с началом в вершине пирамиды или биссекторы всех двугранных углов при ребрах основания пирамиды проходят через одну точку». { В 14-й слайде презентации появляется вторая теорема } После того, как будут сформулированы теоремы, учащимся раздаются листы, на которых эти теоремы уже записаны. Впоследствии ученики должны вклеить их себе на обложку тетради. Для закрепления теории (теорем о сфере вписанной в призму и пирамиду) при фронтальной работе с учащимися решаются задачи № 1, № 2. Ученикам выдаются листы формата А5 (чтобы им удобнее было их потом вклеить в свои тетради), на которых напечатаны, но не полностью, рисунки к задачам. В процессе решения задач учащиеся сами достраивают необходимые элементы. З 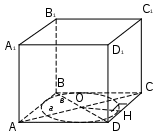 адача №1: Около шара описан прямой параллелепипед, у которого диагонали основания равны а и в. Найти площадь полной поверхности параллелепипеда. (5 мин) адача №1: Около шара описан прямой параллелепипед, у которого диагонали основания равны а и в. Найти площадь полной поверхности параллелепипеда. (5 мин)Дано: АВСDA1B1C1D1 – прямой параллелепипед, в него вписан шар. АС = а, ВD = в. Найти: S п п п П.: Что нам дано по условию задачи? У.: Прямой параллелепипед. П.: На выданных вам листах он уже изображен. Давайте его обозначим АВСDA1B1C1D1 и начнем записывать «Дано:». Что нам еще известно? {По ходу ответов учеников на 15-м слайде появляются соответствующие строки и достраиваются указанные элементы} У.: Что в него вписан шар и диагонали основания равны а и в. П.: Пусть диагональ АС = а, диагональ BD = в. Изобразим их на нашем рисунке. Решение: П.: Какой вывод можно сделать из того, что в параллелепипед вписан шар? У.: В основание можно вписать окружность, и высота параллелепипеда равна диаметру вписанного в него шара. П.: А какой по виду четырехугольник является основанием параллелепипеда? У.: параллелограмм. П.: А когда в параллелограмм можно вписать окружность? У.: Если этот параллелограмм является ромбом. П.: Значит, ABCD – ромб. Давайте запишем наши выводы в первом пункте решения: 1) т.к. в призму вписан шар, то в основания можно вписать окружность, тогда ABCD – ромб. П.: Чему равна площадь полной поверхности параллелепипеда? У.: Сумме площадей оснований и всех боковых граней. П.: А что собой представляют грани прямого параллелепипеда? У.: Прямоугольники. П.: Причем в данном случае, т.к. ABCD – ромб, то все эти прямоугольники равновеликие. Т.о. Sппп будет складываться из 2SABCD и 4SDCC1D1. Т.е.: 2) Sппп = 2SABCD + 4SDCC1D1. П.: А чему равна площадь ромба, если известны его диагонали? У.: Половине произведения диагоналей. П.: Итак, запишем: 3) SABCD = П.: А чему равна площадь прямоугольника DCC1D1? У.: Произведению DC и CC1. П.: А чему равна CC1, если известно, что в параллелепипед вписан шар? У.: диаметру вписанного в него шара. П.: Давайте, изобразим радиус вписанной в основание окружности. Он будет равен радиусу шара, вписанного в параллелепипед. Значит CC1=2ОН. А чему равно произведение DC·2OH относительно основания? У.: Площади основания. П.: А площадь основания мы уже находили. Итак: 4) SDCC1D1 = DC·CC1 = DC·2OH = П.: Подставив полученные значения в формулу из пункта 2), получим: 5) Sппп = 3ab. П.: Запишем ответ: Ответ: Sппп = 3ab. Задача №2 (№ 755): В пирамиду, основанием которой является ромб со стороной а и углом α, вписан шар. Найдите объем шара, если каждая боковая грань пирамиды составляет с плоскостью основания угол β. 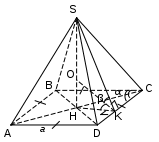 Дано: SABCD – пирамида, ABCD – ромб, AB = a, ﮮBCD = α, ﮮSDCH= β. Шар вписан в пирамиду. Найти: Vшара. П.: Что нам дано по условию задачи? У.: Пирамида, основанием которой является ромб. П.: На выданных вам листах она уже изображена. Давайте ее обозначим SАВСD и начнем записывать «Дано:». Что нам еще известно? {По ходу ответов учеников на 16-м слайде появляются соответствующие строки и достраиваются указанные элементы} У.: Что сторона ромба равна а, ﮮBCD = α, ﮮSDCH= β, шар вписан в пирамиду. П.: Изобразите недостающие элементы на вашем чертеже. Что нам нужно найти? У.: Объем шара. Решение: П.: Какой вывод можно сделать о том, куда спроецируется высота пирамиды, зная, что все ее боковые грани равнонаклонены к плоскости основания? У.: Высота пирамиды спроецируется в точку пересечения биссектрис углов основания, а т.к. в основании – ромб, то высота спроецируется в точку пересечения диагоналей ромба. П.: Верно. Построим высоту SH и запишем сказанное в первом пункте решения: SH - высота: все боковые грани равнонаклонены к плоскости основания, поэтому высота проецируется в точку пересечения биссектрис углов основания, а т.к. в основании – ромб, то высота проецируется в точку пересечения диагоналей ромба. П.: Для того, чтобы найти объем вписанного шара, нам надо найти, чему равен его радиус. Для этого необходимо построить центр шара. А где расположен цент шара, вписанного в пирамиду? У.: На пересечении биссекторов двугранных углов, образованных боковыми гранями и плоскостью основания. П.: В нашем случае все боковые грани равнонаклонены к плоскости основания. Давайте построим один из двугранных углов, образованных боковыми гранями и плоскостью основания, например, двугранный угол с ребром CD. Как будем его строить? У.: Опустим перпендикуляр SK из вершины S к ребру DС, соединим точки Н и К, отрезок НК будет перпендикулярен DС по теореме о трех перпендикулярах. П.: Молодцы! Давайте, запишем это во втором пункте решения: 2) ﮮ SHK= β – линейный угол двугранного угла. П.: Теперь построим биссектрису КО ﮮ SHK. Запишем: КО–биссектриса ﮮSHK, КО∩SH={O},O–центр вписанного шара, ОН–радиус. П.: Часто встречаются задачи, в условии которых дана пирамида, все боковые грани которой равнонаклонены к плоскости основания или условие, эквивалентное этому. Поэтому чтобы построить центр сферы вписанной в такую пирамиду удобно пользоваться схемой. Мы с вами только что построили центр сферы вписанной в такую пирамиду. Давайте, попробуем выделить этапы его построения. Что мы делали сначала? У.: Строили высоту пирамиды. П.: Что потом изображали? У.: Линейный угол двугранного угла при ребре основания. П.: А затем? У.: Изображали его биссектрису. П.: И, наконец? У.: Строили точку пересечения высоты пирамиды с этой биссектрисой. Эта точка и есть центр вписанной сферы. П.: Итак, мы получили следующую схему (17-й слайд): Схема построения центра сферы, вписанной в пирамиду, все боковые грани которой равнонаклонены к плоскости основания 1. Построить высоту пирамиды. 2. Изобразить линейный угол двугранного угла при ребре основания. 3. Изобразить его биссектрису. 4. Точка пересечения высоты пирамиды и этой биссектрисы – центр вписанной сферы. Ученики записывают схему себе на листы (5 мин). П.: Вернемся к решению задачи. Нам требуется найти объем. Чему равен объем шара? У.: V = П.: Верно, запишем это в третьем пункте решения. А из какого треугольника мы сможем найти значение ОН? У.: Из ∆ОНК. П.: А что нам известно в ∆ОНК? У.: Угол OHK = 90°, угол ОКН = П.: Значит, чтобы найти ОН из ∆ОНК, нам еще надо найти, чему равно НК. В задаче № 1 мы выражали площадь ромба двумя способами. Как можно выразить площадь ромба, используя данные задачи № 2? У.:SABCD = П.: Выразив НК, получим: П.: Теперь из ∆ОНК через tg П.: Подставив значение r в формулу объема, получим: П.: Итак, записываем ответ: Ответ: Подведение итогов урока: П.: Что мы изучали сегодня на уроке? У.: Сферу, вписанную в многогранник. П.: О каких теоретических фактах, связанных с ней, вы узнали? У.: О теоремах – необходимых и достаточных условиях того, когда в призму и пирамиду можно вписать сферу, о схеме построения центра сферы, вписанной в пирамиду, у которой все боковые грани равнонаклонены к плоскости основания. Домашнее задание: (19-й слайд) 1) приклеить лист с теоремами на обложку тетради; 2) выучить теоремы и схему построения центра сферы, вписанной в пирамиду, у которой все боковые грани равнонаклонены к плоскости основания. 3) решить задачи: Задача №1: Все ребра треугольной пирамиды равны. Найти отношение радиуса вписанной в пирамиду сферы к ее высоте. 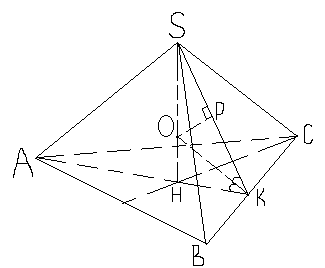 Дано: SABC – пирамида, все ребра которой равны; сфера, вписанная в пирамиду. Найти: Ответ: Задача №2: Основание прямой призмы - прямоугольный треугольник с острым углом α и гипотенузой с. Найдите объем шара, вписанного в эту призму. Ответ: II урок (45 мин.) 1. В качестве актуализации в начале урока для небольшого повторения теорем и дополнительной мотивации при фронтальной или индивидуальной работе по карточкам выполняются задания типа «верно ли утверждение?» Например: 1) Верно ли утверждение: «В любую треугольную пирамиду можно вписать сферу»? Ответ обосновать. 2) Верно ли утверждение: «В любую прямую треугольную призму можно вписать сферу»? Ответ обосновать. 3) Верно ли утверждение: «В любую четырехугольную пирамиду можно вписать сферу»? Ответ обосновать. 4) Верно ли утверждение: «Если в основание призмы можно вписать окружность, то в призму можно вписать сферу»? Ответ обосновать. и другие. (5 мин) 2. Решение более сложных задач, нежели на первом уроке, при фронтальной работе с классом. Учащиеся решение записывают на тех же листах, что им были выданы на первом уроке. (35 мин) Задача № 3. В правильную четырёхугольную пирамиду вписан шар. Расстояние от центра шара до вершины пирамиды равно а, а угол между боковой гранью и плоскостью основания равен α. Найти площадь полной поверхности пирамиды. 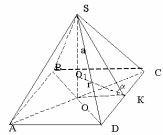 Дано: SABCD – правильная четырёхугольная пирамида, SO1 = a, О1 – центр вписанного в пирамиду SABCD шара. ﮮ(SDC)(АВС)= α. Найти: Sппп Р  ешение: 1) Т.к. О1К – биссектриса ешение: 1) Т.к. О1К – биссектриса Но 2) SO = a + acosα = a(1 + cosα) SK = SO/sinα = a(1 + cosα)/ sinα= 2acos2(α/2)/(2 sin(α/2) cosα(α/2)) = = actg(α/2) OK = SKcosα = actg(α/2) cosα 3) Sосн = AD2 AD = 2OK AD =2 actg(α/2) cosα Sосн = 4a2ctg2(α/2) cos2α 4) Sбп = 4S∆DSC = 2SK∙DC = 2SK∙AD Sбп =2 actg(α/2) ∙2 actg(α/2) cosα = 4a2ctg2(α/2) cosα 5) Sппп = Sбп + Sосн = 4a2ctg2(α/2) cosα(1+ cosα) Ответ: Sппп = 4a2ctg2(α/2) cosα(1+ cosα) Задача № 4. Центр сферы, вписанной в правильную четырехугольную пирамиду, делит ее высоту в отношении т : п, считая от вершины. Найти угол между двумя смежными боковыми гранями. {Эта задача взята из классной работы по элементарной математике} 3. Подведение итогов в виде кроссворда. (4 мин) {См. 20-й слайд презентации} 4. Выдача домашнего задания: (1 мин) – подготовиться к самостоятельной работе; – решить задачи: № 635, № 632, № 634. |
