признаки равенства треугольников. Сформулируйте определение треугольника Какие фигуры называются равными
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Сформулируйте определение треугольника Какие фигуры называются равными? Как определить, равны ли два треугольника? а) наложить друг на друга – равные полностью совместятся; б) измерить и сравнить 6 пар элементов – в равных треугольниках все 6 элементов (3 стороны и 3 угла) одного треугольника будут соответственно равны элементам другого треугольника); Какие условия должны выполняться для того чтобы ∆ АВС = ∆ MNK? стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника. (слайд 2). Назовите для данных треугольников равные элементы. 4. Объяснение нового материала. Для того, чтобы выяснить равны ли треугольники не нужно проверять равенство всех сторон и углов! Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого треугольника. О том, какие эти три элемента расскажут признаки равенства треугольников. Первый признак равенства треугольников (по двум сторонам и углу между ними – три элемента!). (слайд 5) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Попробуйте определить, что является условием, а что заключением теоремы. Условие: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника. Заключение: то такие треугольники равны. Условие записываем в «Дано», заключение в «Доказать» (слайд 6) Чтобы доказать равенство треугольников мысленно совместим их наложением. Какие элементы данных треугольников мы знаем? С какого элемента удобнее начинать наложение? ∠А =∠А₁, АВ = А₁В₁, АС = А₁С₁, Доказательство. Так как ∠А =∠А₁, то ∆ АВC можно наложить на ∆ А₁В₁С ₁ так, что вершина А совместится с вершиной А₁. Поскольку АВ = А₁В₁, АС = А₁С₁, то сторона АВ совместится со стороной А₁В₁, а сторона АС со стороной А₁С₁. (слайд 7) Какие точки при этом совместятся? Поэтому совместятся точки В и В₁,С и С₁ Следовательно совместятся сторона ВС со стороной В₁С₁. Значит, ∆АВC = ∆А₁В₁С ₁, что и требовалось доказать.  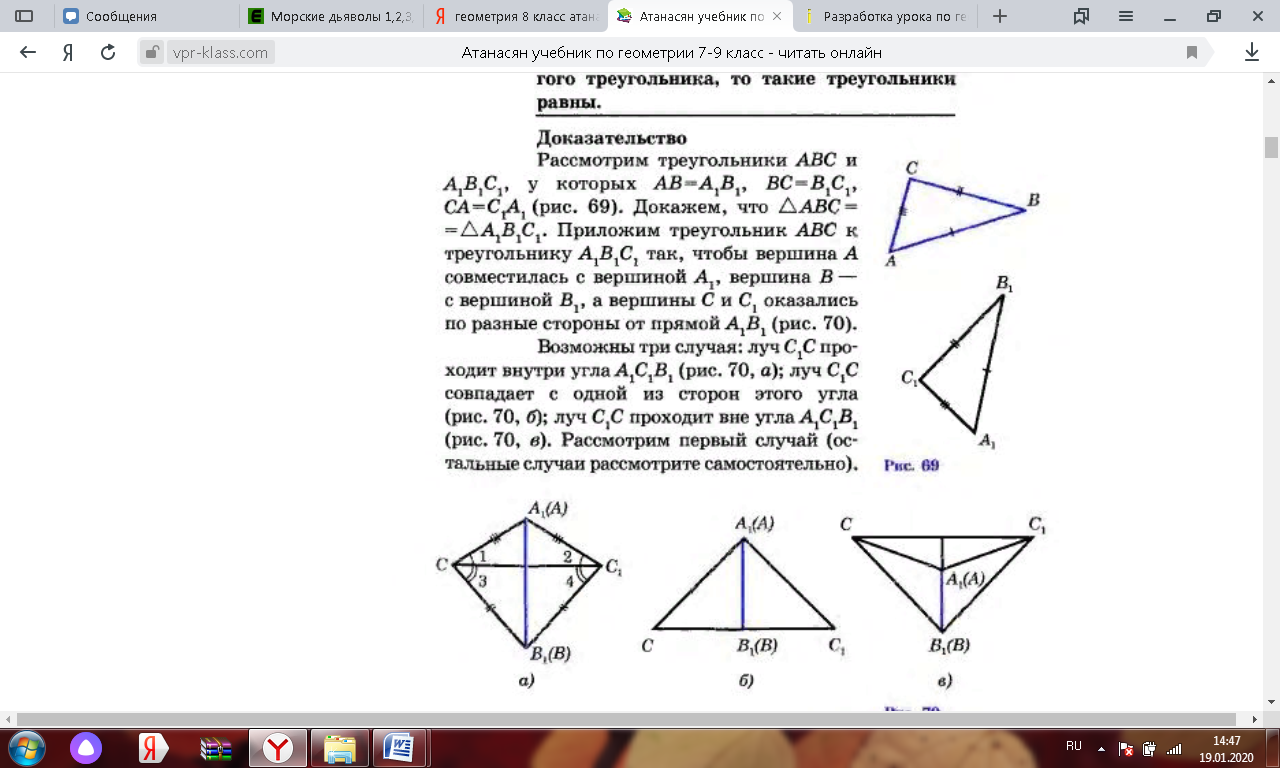   |
