Экзамен линейные системы алгоритмических решений. Экзамен ЛСАР 1-20. Сформулируйте понятие регулирования

Название	Сформулируйте понятие регулирования
Анкор	Экзамен линейные системы алгоритмических решений
Дата	05.11.2020
Размер	1.42 Mb.
Формат файла
Имя файла	Экзамен ЛСАР 1-20.docx
Тип	Закон #148154
страница	3 из 3

1 2 3

Математический признак устойчивости.

Понятие устойчивости можно распространить и на случай движения САУ:

невозмущенное движение,
возмущенное движение.

Определение устойчивости по М. Я. Ляпунову

Невозмущенное движение (при x_i_=0) называется устойчивым по отношению к пременным x_i, если при всяком заданном положительном числе A², как бы мало оно нибыло, можно выбрать другое положительное число ²(A²) так, что для всех возмущений x_i₀, удовлетворяющих условию: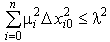

,

возмущенное движение будет для времени tT удовлетворять неравенству: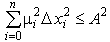

,

где: _i - коэффициенты, уравновешивающие размерности величин x_i₀.

Если с течением времени lim x_i0, то система ассимптотически устойчива.

Понятие о характеристическом уравнении

Было сказано, что устойчивость системы связана с природой самой системы, а не с тем, как внешние источники движущих сил (задание, помехи) заставляют перемещаться ее координаты. Очевидно, что невозможно описать систему не учитывая источников. Поэтому в правой части ДУ описывающих систему всегда будут присутствовать источники движущих сил. Однако если их обнулить, то система ДУ не потеряет смысла. После отключения источников в любой линейной цепи преобразования энергии возникнет переходный процесс обусловленный энергией, которую накопили пассивные реактивные элементы цепи (собственный переходный процесс). Именно он определит, будет ли система устойчивой. И именно эта система ДУ, в которой обнулены величины источников движущих сил, называется характеристической. Если система характеристических ДУ решена относительно одной из координат, то она называется характеристическим уравнением.

Виды соединений звеньев.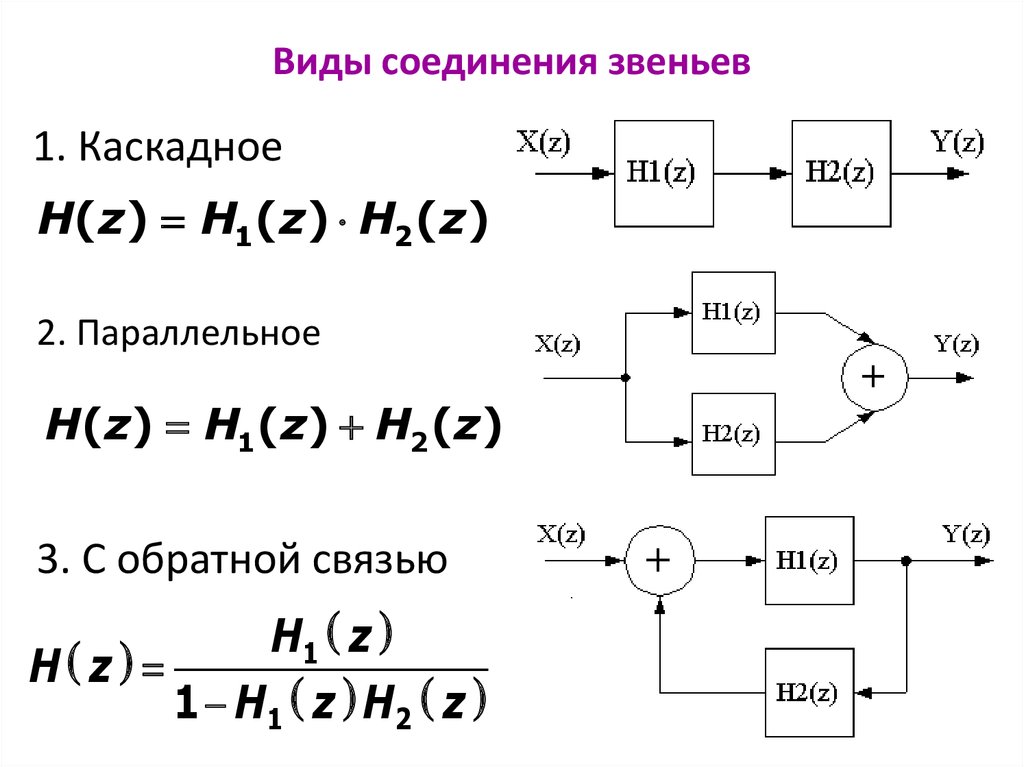

Преобразование схем с использованием переносов ветвлений и сумматоров через звено

Бывают случаи, когда соединение звеньев сложное: и не параллельное, и не последовательное. Такое может быть в многоконтурных схемах с перекрещивающимися связями. В этом случае, для упрощения схем, переносят через звенья узлы ветвления или сумматоры.

Перенос ветвления влево

Узел ветвления из соображений реализуемости результирующей схемы целесообразно переносить через звено влево: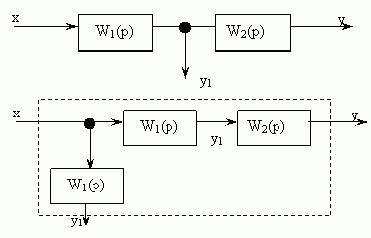

Рис. Эквивалентные схемы. Ветвление перенесено влево через звено W₁(p)

Для сохранения эквивалентности схем, при переносе ветвления влево следует добавить в схему блок с передаточной функцией W₁(p). Тогда в обеих схемах передаточные функции по каналу х → y₁ будет равны:

Y₁(p)= W₁(p) · X(p))

Перенос сумматора вправо

Сумматор из соображений реализуемости результирующей схемы целесообразно переносить вправо: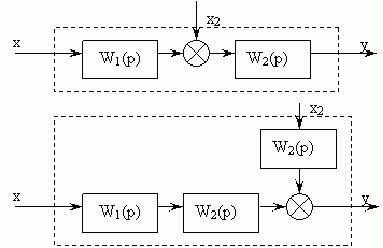

Рис. Эквивалентные схемы. Сумматор перенесен вправо через звено W₂(p)

Для сохранения эквивалентности схем, при переносе сумматора вправо следует добавить в схему блок с передаточной функцией W₂(p). Тогда в обеих схемах выходные сигналы будут одинаковыми:

Y(p)=X(p) · W₁(p) · W₂(p) +X₂(p) · W₂(p)

Уравнение динамики обьектов.

Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся протеканием в ней переходных процессов. Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ.

Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамикиy(t) = F(u,f,t), описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:

F(y, y’, y”,..., y⁽ⁿ⁾, u, u’, u”,..., u^(m), f, f ’, f ”,..., f^(k)) = 0.

Методика составления дифференциальных уравнений

Составление дифференциального уравнения по условию задачи чаще всего состоит в определении математической зависимости между переменными величинами и их приращением [1]. Умение составить дифференциальное уравнение во многом зависит от навыка и понимания решающим физического содержания задачи. Методика составления и решения дифференциального уравнения сводится к следующему: - внимательному и подробному разбору условий задачи и выполнению чертежа; - составлению соотношения между переменными и их приращениями для элементарного акта процесса (то есть процесса, протекающего за малый промежуток времени, или, в общем случае, в течение малого приращения аргумента); - составлению дифференциального уравнения рассматриваемого процесса; - интегрированию составленного дифференциального уравнения и определению его общего решения; - исследованию общего решения; - определению вспомогательных параметров (если они есть по условию задачи); - выводу закона, определению частного решения дифференциального уравнения при заданных начальных условиях и числовому определению искомых величин (если это требуется по условию задачи); - анализу ответа. Составив соотношение между переменными величинами и их приращениями для элементарного акта процесса, переходят к пределу при стремлении приращения аргумента к нулю, получают дифференциальное уравнение в дифференциалах. Интегрирование полученного уравнения позволяет, объединив совокупность элементарных актов процесса, получить зависимость, которой подчиняется данный процесс в целом. Иногда делается ряд допущений, упрощающих задачу, но не отражающихся в результатах. Например, бесконечно малые приращения величин заменяются их дифференциалами. Предполагается, что всякий физический процесс, рассматриваемый в течение бесконечно малого промежутка времени , протекает с постоянной скоростью, и т. д. Кроме того, при составлении дифференциального уравнения задачи, в зависимости от её условия, используются известные законы физики, химии, механики и других наук и различные математические сведения. Обычно для заданных дифференциальных уравнений (или системы уравнений) определяются их решения (прямые задачи теории дифференциальных уравнений; в обратных задачах решения известны и требуется определить неизвестные структуру, порядок и параметры этого уравнений (или системы); эти задачи иначе называются задачами идентификации). С точки зрения соотношения «причина-следствие» задачи математического моделирования условно разделяются на два больших класса: прямые задачи (известны причины, необходимо найти следствия) и обратные (известны следствия, нужно найти причины). Обычно обратными задачами называются задачи, решение которых состоит в определении причинно-следственных связей в рамках некоторой математической модели исследуемого объекта или процесса (определяются параметры данной модели по имеющимся результатам наблюдений и прочей экспериментальной информации).

Линеаризация уравнений разложением в ряд Тэйлора

Классификация САУ по алгоритму управления. Поисковые САР.

По алгоритму управления.

Принцип программного управления, когда алгоритм управления вырабатывается по заранее составленной программе в задающем устройстве и последовательно выдается на объект управления.

В таких САУ вся информация об управлении априорно (заранее) занесена в задающее устройство. По такому принципу работают станки с числовым программным управлением для получения ткани с вышитым рисунком, светофоры на перекрестках и т.д.

Принцип управления по возмущению, когда алгоритм управления вырабатывается с помощью датчика возмущающего воздействия и компенсирует вызываемое им отклонение регулируемой величины.

В таких САУ вся информация об управлении на регулятор поступает с возмущающего воздействия. Обычно это нагрузка. По такому принципу работают, например, генераторы с дополнительной обмоткой возбуждения в цепи якоря, в которой создается дополнительный магнитный поток для компенсации потери напряжения, который пропорционален силе тока нагрузке генератора.

Принцип управления по отклонению, когда алгоритм управления вырабатывается по отклонению между заданным и действительным значением регулируемой величиной.

В таких САУ информация определяется с помощью датчика регулируемой величины, сравнивается с заданным и пропорционально ошибке происходит процесс регулирования. Особенность такой САУ – наличие главной обратной связи от регулируемой величины на регулятор. По такому принципу работают большинство САУ для регулирования температуры, давления, частоты вращения двигателей и т.д.

Принцип комбинированного управления, когда алгоритм управления вырабатывается одновременно и по возмущению и по отклонению

Такие САУ имеют два контура управления. В первом контуре (по возмущению) производится быстрое предварительное регулирование, а во втором контуре (по отклонению) производится медленная и точная регулировка. По такому принципу происходит регулирование, например, давление пара в паровом котле. Пропорционально расходу пара производится регулирование по возмущению (по нагрузке), а по отклонению давления пара от заданного производится более точное регулирование.

Основное преимущество самонастраивающихся систем сводится к тому, что они автоматически приспосабливаются к изменяющимся условиям работы и автоматически находят успешный (в заранее заданном смысле) режим работы. Еслп системе дается задание, чтобы какая-то определенная функция ее координат была экстремальной (напр., наибольшая степень хпмич. превращения, наименьшее накоилетпю побочных продуктов и т. п.), то она наз. системой оптимизации (или с экстремальным регулированием). Самонастраивающиеся системы включают различные счетно-решающие устройства, позволяющие автоматически осуществлять различные (порой очень сложные) математич. операции. В самонастраивающихся системах чаще всего исиользуется принцип автоматич. поиска, заключающийся в осуществлении пробных воздействий на управляемый процесс до тех пор, пока не будут выработаны такие управляющие воздействия, к-рые позволили бы реализовать заданный ход процесса. В отличие от метода ирименения заранее заданного точного алгоритма управления (в т, н. аналитических, вычислительных САР), метод поиска не требует полного математич. описания управляемого объекта и условий его работы

поисковых С. с. необходимое качество управления достигается в результате автоматического поиска оптимальной (в некотором смысле) настройки (см. Поисковая система). Качество настройки характеризуется некоторым обобщённым показателем, связанным с первичными параметрами настройки сложным, обычно не вполне стабильным и недостаточно известным соотношением. Этот показатель измеряется непосредственно или вычисляется по измеренным значениям первичных параметров. Параметрам настройки в С. с. придаются поисковые или пробные изменения. Анализ колебаний показателя качества настройки, вызванных поисковыми воздействиями, позволяет установить, является ли настройка оптимальной, т. е. соответствующей экстремуму (максимуму или минимуму) показателя качества. Если имеют место отклонения от экстремума, то настройка изменяется до тех пор, пока не приблизится к оптимальной.

Классификация САУ по алгоритму управления.

Сформулируйте понятие регулирования.
Сформулируйте понятие управление.
Сформулируйте понятия системы автоматического регулирования.
В чем заключается смысл управления?
Что называют автоматическим управлением?
Приведите пример управляющих воздействий.
Назовите основные типы задач управления.
Приведите основные принципы регулирования.
Математическое описание линейных систем.
Разомкнутые системы управления
Замкнутые системы упрваления.
Комбинированные системы управления.
Физическое и математическое моделирование.
Понятие об устойчивом процессе.
Виды соединений звеньев.
Уравнение динамики обьектов.
Методика составления дифференциальных уравнений.
Линеаризация уравнений разложением в ряд Тэйлора
Классификация САУ по алгоритму управления. Поисковые САР.
Классификация САУ по алгоритму управления. Беспоисковые САР.

1 2 3