Экзамен линейные системы алгоритмических решений. Экзамен ЛСАР 1-20. Сформулируйте понятие регулирования

• Название: Сформулируйте понятие регулирования
• Анкор: Экзамен линейные системы алгоритмических решений
• Дата: 05.11.2020
• Размер: 1.42 Mb.
• Имя файла: Экзамен ЛСАР 1-20.docx
• Тип: Закон; #148154
• страница: 2 из 3

Принципы автоматического регулирования

Системы автоматического регулирования предназначены для того, чтобы поддерживать управляемую величину объекта пропорциональной задающей величине с требуемой точностью. Т.о., закон изменения во времени задания повторяется управляемой величиной. Задание, как правило, маломощный сигнал. САР позволяет с помощью этого маломощного сигнала управлять мощным объектом.

По принципу управления САУ можно разбить на четыре группы:

1. 
   С регулированием по внешнему воздействию - принцип Понселе (применяется в незамкнутых САУ).
   
2. 
   С регулированием по отклонению - принцип Ползунова-Уатта (применяется в замкнутых САУ).
   
3. 
   С комбинированным регулированием. В этом случае САУ содержит замкнутый и разомкнутый контуры регулирования.
   
4. 
   Системы экстремального управления.
   

Принцип управления по внешнему возмущению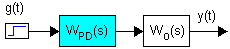

А) разомкнутая САР с жестким управлением

Схема используется для программного управления.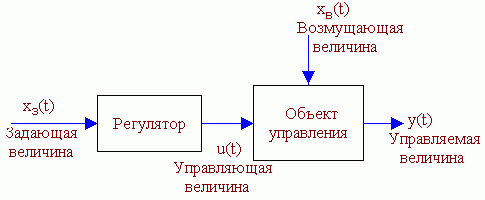

Б) разомкнутая САР с управлением по возмущению

Схема используется для программного управления и стабилизации.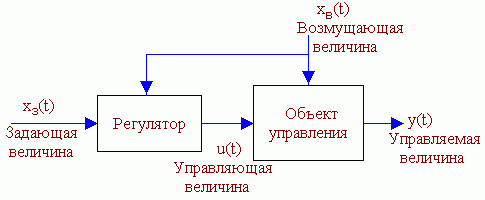



Функциональная схема разомкнутой САР с управлением по возмущению. Управляющее воздействие u формируется регулятором на основе задания х_з(t) и с учетом возмущения х_в(t).

Принцип управления по отклонению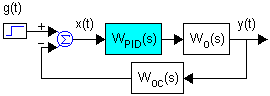

Замкнутая САР с управлением по отклонению

Схема используется для слежения, программного управления и стабилизации.

В такой системе регулятор в процессе управления учитывает как задание, так и реальное состояние объекта, а, кроме того, косвенно учитывает и возмущение.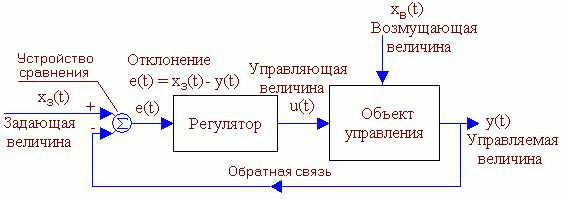



Функциональная схема замкнутой САР с управлением по отклонению. e(t) – отклонение (ошибка слежения, регулирования) управляемой величины y(t) от задания х_з(t). Основные элементы схемы: объект управления, контур главной обратной связи

Сравнивающее устройство (сумматор) сравнивает задающую и управляемые величины и вычисляет отклонение, ошибку e(t) = х_з(t) - y (t).

Регулятор – вырабатывает такое управляющее воздействие u(t) на объект управления, которое сводит ошибку к нулю или допустимому минимуму. В идеале, когда e = 0, х_з(t) = y (t)

Комбинированное управление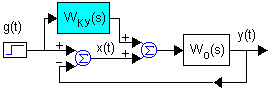

Комбинированная схема с управлением по отклонению и возмущению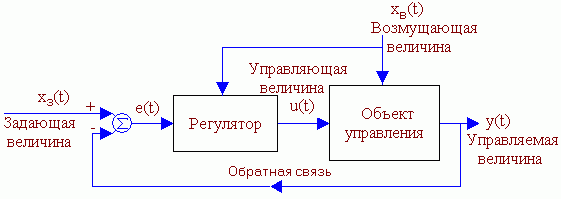

Функциональная схема САР с комбинированным управлением по отклонению и по возмущению

Системы экстремального управления

Принцип управления: (буровой станок)

Оптимальная скорость бурения достигается тогда, когда производная скорости по давлению на долото равна нулю. Отклонение давления от оптимального значения приводит к появлению положительной или отрицательной производной скорости по давлению, что позволяет регулятору вырабатывать сигнал компенсации, который определяет направление изменения давления на долото.

9. 
   Математическое описание линейных систем.
   

Целью рассмотрения системы автоматического управления является решение одной из двух задач: анализа или синтеза системы. При анализе системы требуется определить свойства системы с заданными значениями параметров, при синтезе - создать систему, удовлетворяющую заданным требованиям. В общем виде порядок исследования в обоих случаях включает в себя математическое описание системы, исследование ее установившихся и переходных режимов.

Математическое описание, т.е. получение математической модели, начинается с разбиения системы на звенья и описание этих звеньев. По уравнениям или характеристикам отдельных звеньев составляют уравнения или определяют характеристики системы в целом, на основании которых ее исследуют.

Звеном называют часть системы, которая осуществляет преобразование входной величины в выходную. Звено обладает свойством однонаправленности, т.е. предыдущее звено воздействует на последующее. Разбиение системы на звенья может не совпадать с разбиением системы на функциональные элементы.

Звено - это условно выделенный направленного действия преобразователь сигналов, который может быть частью элемента или состоять из нескольких таких элементов.

Если разбить систему на звенья направленного действия, то математическое описание каждого звена может быть выполнено без учета его связей с другими звеньями системы. При этом математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений звеньев системы и уравнений связи между звеньями.

Уравнениями связи называют уравнения, отражающие характер передачи воздействий между звеньями системы.

После разбиения САУ на звенья направленного действия и получения математического описания звеньев составляют структурную схему. Структурной схемой САУ называется схема, показывающая, из каких звеньев состоит система и как эти звенья соединены между собой. На структурной схеме звенья изображаются прямоугольниками, а связи между звеньями и внешние воздействия – стрелками. Каждому звену структурной схемы соответствует описывающее его уравнение или характеристика. Получение структурной схемы является конечной целью математического описания.

Различают два вида характеристик звеньев: статические и динамические. Статическая характеристика звена представляет собой зависимость между входной Х_вх и выходной Х_вых величинами в установившемся режиме при разных постоянных значениях внешнего воздействия f (t)= f . В общем случае эта зависимость является нелинейной.

Если на находящееся в некотором состоянии звено (систему) влияет возмущающее воздействие, то звено начинает переходить в некоторое другое состояние. Характер процесса перехода звена (системы) из одного состояния в другое определяется динамической характеристикой звена (уравнением движения). Уравнение движения - это дифференциальное уравнение, определяющее изменение во времени выходной величины звена по заданному изменению во времени его выходной величины.

В теории автоматического управления общее дифференциальное уравнение звена (системы) принято записывать в следующем виде: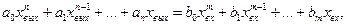



где m и n - числа, показывающие высший порядок производных от входной величины 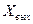  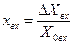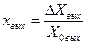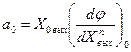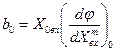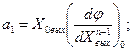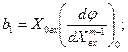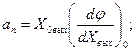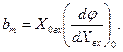и выходной величины   ;

 ;   ;

 ;   ;

 

 

В большинстве случаев m < n. Число n называется порядком дифференциального уравнения.

Если динамика звена описывается линейным дифференциальным уравнением, то это звено называется линейным, если дифференциальное уравнение нелинейное, то звено называют нелинейным. Целью исследования любой САУ является анализ ее динамики и статики или синтез. При анализе задана структура САУ и ее параметры. Необходимо исследовать свойства САУ. Задача синтеза наиболее сложная. При синтезе разрабатывается управляющая часть САУ, включая в общем случае выбор принципа управления, типа схемы и параметров управляющего устройства, т.е. заданы свойства - требуется создать САУ.

Для решения этих задач необходимо математическое описание САУ, т.е. получение ее математической модели. При этом САУ, разнообразные по своему конструктивному исполнению и назначению, могут описываться одинаковыми дифференциальными уравнениями.

Любая система автоматического управления представляет собой совокупность отдельных, взаимодействующих друг с другом элементов соединенных между собой связями. Первым этапом при составлении дифференциальных уравнений является разделение системы на отдельные элементы и составление дифференциальных уравнений этих элементов. При этом систему разбивают на возможно более простые (мелкие) звенья, но так, чтобы каждое звено обладало направленностью действия.

В результате разбиения САУ на звенья направленного действия и получения математического описания звеньев составляется структурная схема системы, в которой каждой математической операции преобразования сигнала соответствует определенное звено.

Структурная схема САУ характеризует ее геометрию, т.е. показывает, из каких элементов состоит САУ, как эти элементы связаны между собой, а так же содержит математическое описание этих элементов.

САУ, какой бы сложной не была, структурная схема ее состоит из четырех типов структурных элементов:

1. 
   структурных элементов направленного действия, представляющих линейные звенья и нелинейные преобразователи, если САУ нелинейная;
   
2. 
   элементов сравнения или сумматоров, в которых происходит сложение или вычитание сигналов;
   
3. 
   точек разветвления или узлов, в которых путь распространения сигналов разветвляется на несколько путей, ведущих к различным точкам системы;
   
4. 
   связей или линий, указывающих направления распространения сигналов.
   

Составленная таким образом структурная схема позволяет не только облегчить задачу исследования, но и наметить последовательность операций анализа и синтеза. Особенно это ценно, если исследования проводятся на ЦВМ. В этом случае наличие структурной схемы значительно упрощает алгоритмизацию процесса решения систем дифференциальных уравнений, описывающих САУ. В некоторых случаях анализ и синтез САУ без структурного представления становится просто невозможным.

Таким образом, составление структурной схемы является завершающим и наиболее важным этапом математического описания САУ. В результате наглядно отображаются не только взаимосвязи в математической модели, но и предоставляется возможным наметить эффективные пути решения задач анализа и синтеза САУ.

10. 
    Разомкнутые системы управления
    

Система, в которой выходной сигнал не подаётся на управляющее устройство, называется разомкнутой.

В разомкнутой системе управления для получения желаемой реакции ОУ обычно используется исполнительное устройство (рис.1.1).



Рис.1.1 Разомкнутая система управления (без обратной связи)

Примером может служить разомкнутая система управления скоростью вращения диска, представленная на рис. 1.2. Во многих современных приборах используется диск, который должен вращаться с постоянной скоростью. В этой системе для задания напряжения, пропорционального желаемой скорости, использована батарея, затем это напряжение усиливается и подаётся на электродвигатель. Электродвигатель постоянного тока, скорость которого пропорционально приложенному напряжению, обеспечивает вращение диска.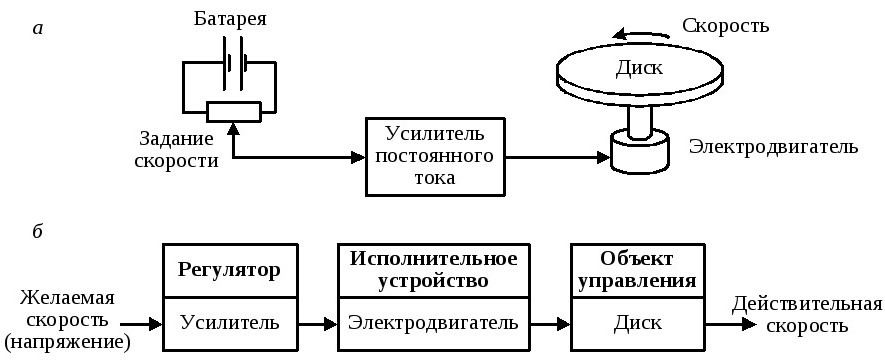



Рис. 1.2 Разомкнутая система управления скоростью вращения диска
 Разомкнутая система:

При использовании разомкнутой системой управления напряжение U_у регулируется с помощью потенциометра или другого устройства. При разомкнутом управлении выходное напряжение  U_я не отслеживается и считается что оно пропорционально заданному U_у.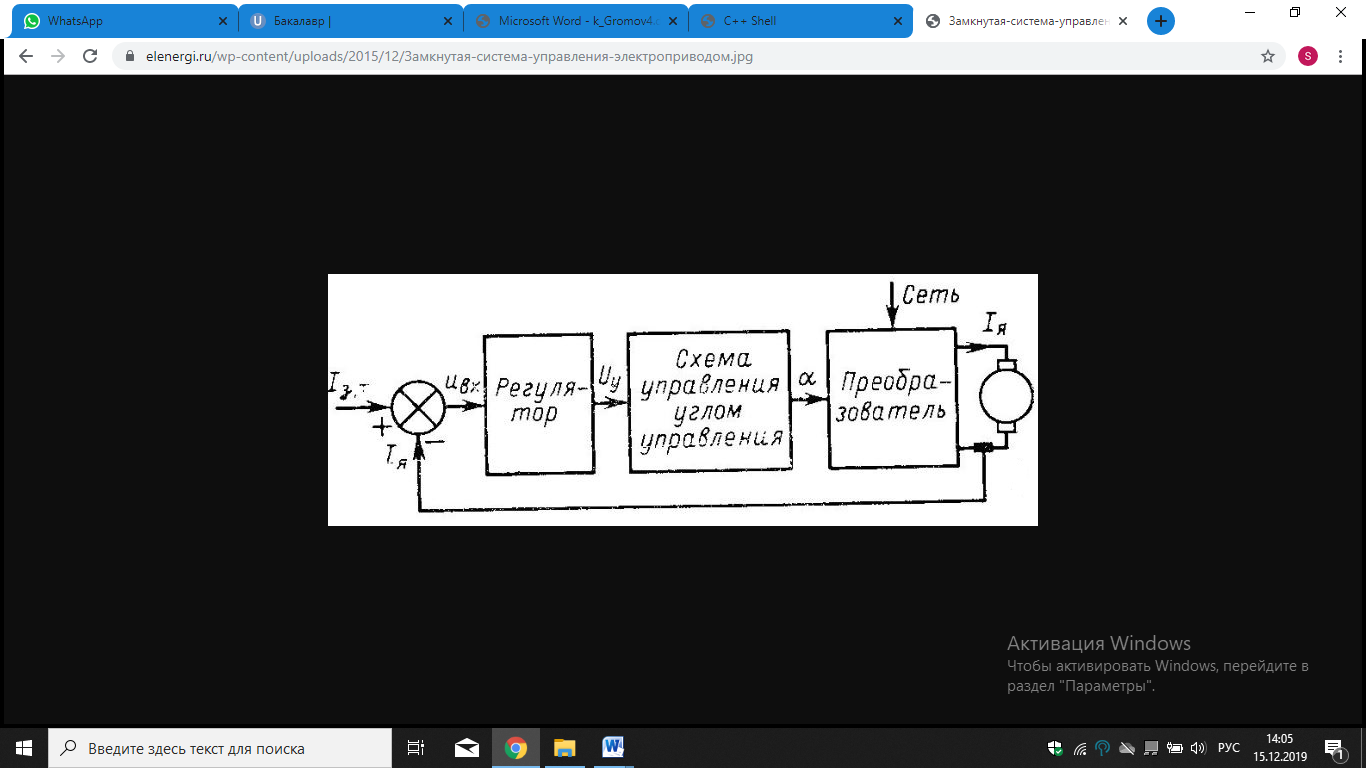



При использовании замкнутых систем управления U_у будет представлять из себя разность между сигналом задания и сигналом, пропорциональным регулируемой координате. При регулировании тока:

Здесь формирование сигнала управления U_у будет представлять собой разницу между реальным током якоря и заданием по току, приходящему из вне.

11. 
    Замкнутые системы упрваления
    

Система, в которой происходит измерение выходной переменной и сравнение её с заданным значением, называется замкнутой.

Измеренное значение выхода называют сигналом обратной связи.

Простейшая замкнутая система изображена на рис 1.3.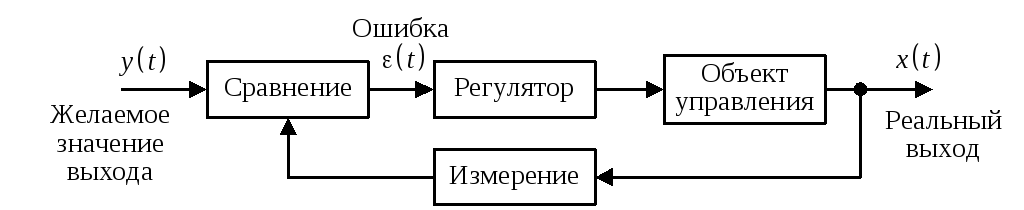



Рис.1.3 Замкнутая система управления (с обратной связью)

В замкнутой системе вычисляется разность (ошибка) между желаемым значением выходной переменной и её измеренным действительным значением.

На рис. 1.4 представлена замкнутая система управления скоростью вращения диска.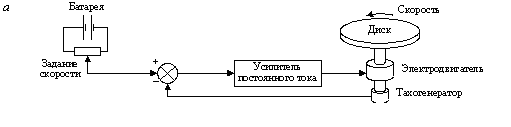



Рис. 1.4Замкнутая система управления скоростью вращения диска

В уже имеющуюся систему необходимо ввести датчик, измеряющий скорость вращения вала двигателя, и устройство для сравнения заданной скорости вращения диска и действительной. Для этих целей удобно использование тахогенератора, выходное напряжение которого пропорционально скорости вращения вала двигателя. Сигнал ошибки образуется как разность между входным напряжением и напряжением тахогенератора. Замкнутая система всегда стремиться свести ошибку к минимуму.

Замкнутые системы автоматического управления (САУ) отличаются от разомкнутых применяемой аппаратурой и полнотой автоматизации. В разомкнутой САУ задающее устройство (включающая, регулирующая аппаратура) не получает информацию о фактическом режиме работы электроустановки (приводного электродвигателя, рабочей машины).

В замкнутой САУ информация передается на элементы управления, что сопровождается подачей соответствующих командных сигналов. Цепочка, передающая такую информацию, замыкает контур управления, образуя замкнутую САУ, или САУ с обратными связями.

Различие между замкнутой и разомкнутой САУ можно пояснить па примере регулирования скорости электродвигателя в системе генератор — двигатель (Г—Д). В разомкнутой САУ (рис. 1,а) заданная скорость электродвигателя устанавливается вручную потенциометром П. Контроль скорости осуществляется визуально по тахометру, получающему питание от тахогенератора ТГ. Всякое отклонение скорости от заданной оператор устраняет воздействием на движок потенциометра.

В замкнутой САУ (рис. 1,б) якорь тахогенератора ТГ включен в цепь обмотки возбуждения генератора ОВГ, создавая замкнутую систему, или систему с обратной связью (в данном случае с обратной связью по скорости).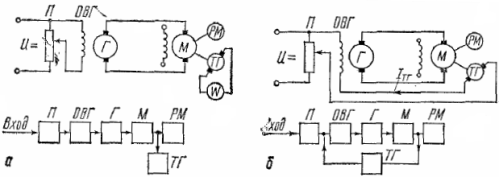



Рис. 1. Схема регулирования электродвигателя в системе Г- М: а - разомкнутая САУ, б - замкнутая САУ

Ток, создаваемый тахогенератором (Iтг) в замкнутой цепи, направлен навстречу току потенциометра (Iп), и в цепи действует результирующий ток, равный геометрической разности этих токов. Движком потенциометра оператор устанавливает такое значение результирующего тока в обмотке возбуждения ОВГ, при котором обеспечивается соответствующая скорость электродвигателя. На этом роль оператора заканчивается. В дальнейшем система автоматически с определенной точностью поддерживает заданный режим работы электропривода.

Допустим, что в результате наброса нагрузки скорость электродвигателя уменьшилась по сравнению с заданной. Уменьшение скорости сопровождается соответствующим уменьшением скорости тахогенератора и напряжения на его зажимах. Это в свою очередь вызовет уменьшение тока Iтг в цепи обратной связи и в определенном положении движка потенциометра — увеличение результирующего тока в обмотке возбуждения генератора. Соответственно возрастут напряжение на генераторе и скорость электродвигателя.

Процесс увеличения скорости и напряжения будет продолжаться до тех пор, пока ток в цепи обратной связи не достигнет установленного значения, а скорость электродвигателя — заданной величины.

12. 
    Комбинированные системы управления.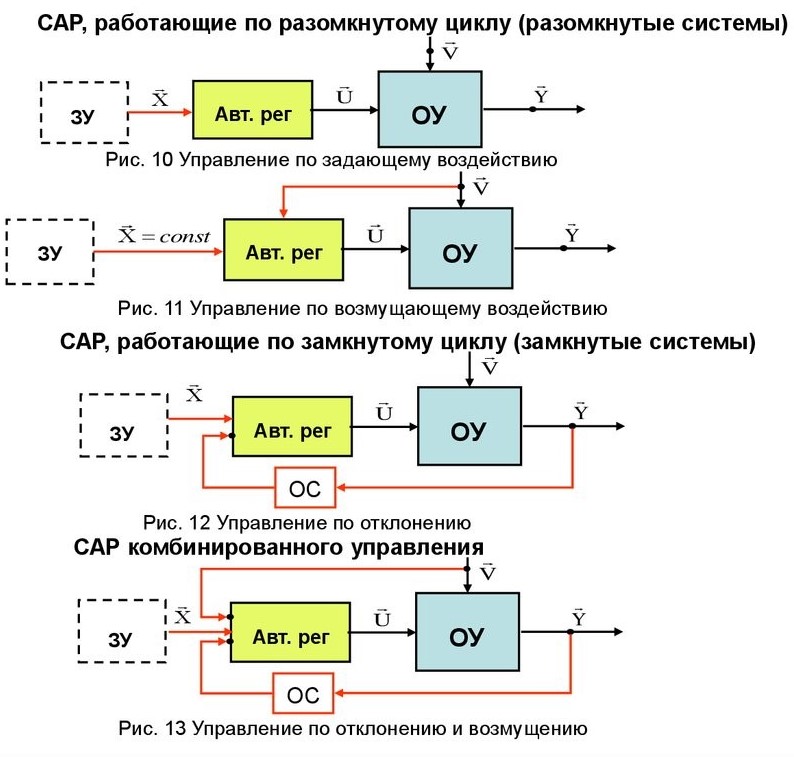
    

Комбинированные системы автоматического регулирования состоят из сочетающихся систем регулирования и управления. Постоянное значение регулируемого параметра поддерживается воздействием по возмущению. В системе с воздействием по возмущению регулятор работает с опережением, т.е. начинает действовать сразу вслед за возмущающим воздействием до момента изменения регулируемого параметра, который контролируется, а изменение сигнала подается на вход регулятора. Кроме того, вводится задающее воздействие, зависящее от возмущения. В комбинированных системах автоматического регулирования ( КСАР) одновременно используются принципы регулирования по отклонению и по возмущению. В КСАР основное регулирование осуществляется при помощи разомкнутых контуров по главному возмущению, а система регулирования по отклонению устраняет ошибку компенсации.  [2]

Наиболее совершенными являются комбинированные системы автоматического регулирования.  [3]

Результатом действия описанной здесь комбинированной системы автоматического регулирования дозы реагента является весьма точная стабилизация величины рН умягченной воды. Это позволяет проводить процесс декарбонизации с заданными скоростью и полнотой при минимальном расходе извести. Вся аппаратура, использованная в системе регулирования, выпускается отечественной промышленностью и, следовательно, может широко применяться на существующих и проектируемых станциях водоподготовки.  [4]

В частности, в случае комбинированных систем автоматического регулирования X ( D) обычно являются коэффициентами, структура которых представляет собой разность двух величин, одна из них определяется воздействием по возмущению. Эти коэффициенты характеризуют одновременно условия связей по возмущению, а именно - необходимость их измерения, а часто и дифференцирования. При нескольких внешних возмущениях число условий инвариантности равно числу зависимых внешних возмущений.  [5]

13. 
    Физическое и математическое моделирование.
    

Физи́ческое модели́рование — метод экспериментального изучения различных физических объектов или явлений, основанный на использовании модели, имеющей ту же физическую природу, что и изучаемый объект^[1].

Метод заключается в создании лабораторной физической модели явления в уменьшенных масштабах и проведении экспериментов на этой модели. Выводы и данные, полученные в этих экспериментах, распространяются затем на явление в реальных масштабах.

Метод применяется при следующих условиях:

• 
  Исчерпывающе точного математического описания явления на данном уровне развития науки не существует, или такое описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно.
  
• 
  Воспроизведение исследуемого физического явления в целях эксперимента в реальных масштабах невозможно, нежелательно или слишком затратно (например, цунами).
  

Метод может дать надёжные результаты, лишь в случае соблюдения геометрического и физического подобия реального явления и модели.

В широком смысле, любой лабораторный физический эксперимент является моделированием, поскольку в эксперименте наблюдается конкретный случай явления в частных условиях, а требуется получить общие закономерности для всего класса подобных явлений в широком диапазоне условий. Искусство экспериментатора заключается в достижении физического подобия между явлением, наблюдаемым в лабораторных условиях и всем классом изучаемых явлений.

изическое моделирование позволяет разработчику создавать модели, которые могут быть использованы многократно и совместно с другими инженерами. Возможность импортировать данные и модели из других сред разработки помогает обеспечить точность моделей. Благодаря интеграции этих моделей с алгоритмами управления и обработки сигналов разработчик может проверить ошибки интеграции в начале процесса проектирования. Моделирование физическое, вид моделирования, который состоит в замене изучения некоторого объекта или явления экспериментальным исследованием его модели, имеющей ту же физическую природу.

  В науке любой эксперимент, производимый для выявления тех или иных закономерностей изучаемого явления или для проверки правильности и границ применимости найденных теоретическим путём результатов, по существу представляет собою моделирование, т. к. объектом эксперимента является конкретная модель, обладающая необходимыми физическими свойствами, а в ходе эксперимента должны выполняться основные требования, предъявляемые к М. ф. В технике М. ф. используется при проектировании и сооружении различных объектов для определения на соответствующих моделях тех или иных свойств (характеристик) как объекта в целом, так и отдельных его частей. К М. ф. прибегают не только по экономическим соображениям, но и потому, что натурные испытания очень трудно или вообще невозможно осуществить, когда слишком велики (малы) размеры натурного объекта или значения других его характеристик (давления, температуры, скорости протекания процесса и т. п.).

  В основе М. ф. лежат подобия теория и размерностей анализ. Необходимыми условиями М. ф. являются геометрическое подобие (подобие формы) и физическое подобие модели и натуры: в сходственные моменты времени и в сходственных точках пространства значения переменных величин, характеризующих явления для натуры, должны быть пропорциональны значениям тех же величин для модели. Наличие такой пропорциональности позволяет производить пересчёт экспериментальных результатов, получаемых для модели, на натуру путём умножения каждой из определяемых величин на постоянный для всех величин данной размерности множитель — коэффициент подобия.

Математи́ческаямоде́ль — математическоепредставлениереальности^[1], один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки эмпирических законов, гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект или процесс, построенный на этапе содержательного моделирования^[⇨]. Математическая модель позволяет предсказать поведение реального объекта.

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

По Ляпунову, математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определённых отношениях и дающая при её исследовании, в конечном счёте, информацию о самом моделируемом объекте^[2].

В других вариантах, математическая модель определяется как объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала^[3], как «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям»^[4], как систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого, исследование которых средствами математики должно ответить на поставленные вопросы о свойствах некоторой совокупности свойств объекта реального мира^[5], как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе^[6].

В автоматизированных системах управления математическая модель используется для определения алгоритма функционирования контроллера. Этот алгоритм определяет, как следует изменять управляющее воздействие в зависимости от изменения задающего для того, чтобы была достигнута цель управления.

Для построения любой математической модели необходимы данные. Базовые знания о строении и функционировании организма человека можно найти в анатомических атласах и другой справочной литературе.

14. 
    Понятие об устойчивом процессе.
    

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Основы теории устойчивости САУ были заложены А.М. Ляпуновым в его работе "Общая задача устойчивости движений", опубликованной в 1882 г.

В статическом режиме работы все составляющие вектора состояния САУ не зависят от момента времени их рассмотрения и остаются постоянными, соответствующими условию равновесия системы. Это состояние в зависимости от структуры и параметров САУ может быть устойчивым или неустойчивым.

Если после изменения вектора внешних воздействий система приходит в состояние, при котором все составляющие вектора ее состояния становятся постоянными, то есть система возвращается в положение равновесия, то это состояние равновесия является устойчивым.

В случае, когда после изменение входного сигнала или возмущения, система не стремится в первоначальное состояние, а вектор выходных сигналов изменяется независимо от внешнего воздействия, то такое состояние является неустойчивым. В этом случае система автоматического управления является неустойчивой. Графическая интерпретация таких режимов работы САУ представлена на рис.



Рис. Графическая интерпретация устойчивости.

Под устойчивостью понимается свойство САУ возвращаться в исходное состояние после вывода ее из этого состояния и прекращения влияния задающего или возмущающего воздействия.

Только устойчивая система автоматического управления может выполнять возложенные на нее функции. Поэтому одной из основных задач САУ является обеспечение ее устойчивости.

Если САУ представляется системой линейных дифференциальных уравнений, то ее устойчивость не зависит от величины и точки приложения внешних возмущений.

Нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших возмущениях. Теорема Ляпунова устанавливает, что об устойчивости нелинейных систем при малых возмущениях можно судить по их линеаризованным уравнениям, достаточно адекватно описывающих поведение САУ при малых отклонениях от положения равновесия. Поэтому будем рассматривать только вопросы устойчивости САУ, представляемых линейными или линеаризованными дифференциальными уравнениями.