+++Колданбалы есептерди шыгарудын погико-психологиялык негиздери. Шаблон для закрытых вопросов (пять вариантов ответов) Примечание в таблице запрещается добавлять удалять строки, колонки, разбивать или объединять ячейки, менять "шапку таблицы". Сокращение
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Оптика | 3 | МӨЖ | ||||
| | A | | Френель | | | |
| | B | | Борн | | | |
| | C | + | Ньютон | | | |
| | D | | Эйнштейн | | | |
| | E | | Фарадей | | | |
| 255 | Т | | Нәрсе оптикалық күші 2,5 дптр линзадан 50см қашықтықта орналасқан.Егер нәрсені линзаға 5см жақындатса, онда оның кескіні ... есе үлкейеді. | Оптика | 1 | МОӨЖ |
| | A | | 0,5 | | | |
| | B | | 1,1 | | | |
| | C | | 0,1 | | | |
| | D | | 1,2 | | | |
| | E | + | 2 | | | |
| 256 | Т | | Линзаның көмегімен экранда нәрсенің кескіні алынды. Егер линзаның астыңғы бөлігін жапса, онда кескін ... | Оптика | 1 | МӨЖ |
| | A | | кескін мүлде жоғалып кетеді. | | | |
| | B | | кескіннің үстіңгі бөлігі жоғалады. | | | |
| | C | | кескіннің астыңғы бөлігі жоғалады. | | | |
| | D | + | кескін орнында қалады, бірақ жарықтылығы азаяды. | | | |
| | E | | кескіннің ортаңғы бөлігі жоғалады. | | | |
| 257 | Т | | Қос дөңес линзаның көмегімен нәрсенің жалған кескіні алынған.Төмендегі формулалардың ішінде осы жағдайға сәйкес келетіні: | Оптика | 3 | МӨЖ |
| | A | | 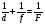 | | | |
| | B | | 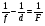 | | | |
| | C | | 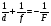 | | | |
| | D | + | 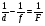 | | | |
| | E | | 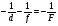 | | | |
| 258 | Т | | Төмендегі приборлардың ішінде нәрсенің нақты және кішірейтілген кескінін беретіні: | Оптика | 3 | МОӨЖ |
| | A | | Микроскоп | | | |
| | B | | Телескоп | | | |
| | C | | көру трубасы | | | |
| | D | + | фотоаппарат | | | |
| | E | | Фильмоскоп | | | |
| 259 | Т | | Екі ортаны бөліп тұрған шекара бетіне түсу бұрышының 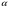 қандай да бір мәнінде түсу бұрышы синусының сыну бұрышы синусына қатынасы қандай да бір мәнінде түсу бұрышы синусының сыну бұрышы синусына қатынасы 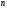 -ге тең. Түсу бұрышын 2 есе арттырса, осы қатынастың мәні: -ге тең. Түсу бұрышын 2 есе арттырса, осы қатынастың мәні: | Оптика | 1 | МОӨЖ |
| | A | | 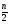 | | | |
| | B | + | 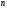 | | | |
| | C | | 2 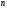 | | | |
| | D | | 4 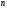 | | | |
| | E | | 9 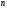 | | | |
| 260 | Т | | Жарықтың электромагниттік теориясын ұсынған: | Оптика | 3 | МӨЖ |
| | A | | Араго | | | |
| | B | | Планк | | | |
| | C | | Эйнштейн | | | |
| | D | + | Максвелл | | | |
| |
