Задания 5 класс. Школьный этап
 Скачать 54.5 Kb.
|
|
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ 2022/2023 учебный год ШКОЛЬНЫЙ ЭТАП МАТЕМАТИКА 5 КЛАСС Написать один ответ мало! Все ответы должны быть объяснены с помощью рассуждений или вычислений! условия задач1. У Вовочки в двух копилках вместе 200 монет. Когда он вытряс из первой копилки 30 монеток, а из второй 40, то в копилках осталось поровну монет. Сколько монет было в каждой копилке первоначально? 2. Волшебник за 100 изумрудов увеличивает имеющийся рост в 2 раза, а колдун за 20 изумрудов увеличивает рост на 25 см. У гнома только 300 изумрудов. Может ли он стать пятиметровым великаном, если сейчас его рост равен 50 см? 3. Разрежьте прямоугольник 7×8 клеточек на 7 квадратов (необязательно одинаковых) по линиям сетки. Достаточно указать один такой способ разрезания. 4. Билет называется «счастливым», если сумма первых трёх цифр номера равна сумме последних трёх цифр, иначе – «несчастливым». Например, билет с номером 015123 – «счастливый». Кондуктор выдал Маше билет с номером 017364. Сколько «несчастливых» билетов ещё продаст кондуктор до ближайшего счастливого билета? Билеты кондуктор продаёт только по порядку номеров, т.е. номер следующего билета после Машиного – 017365. 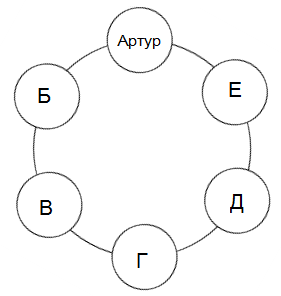 5. Король Артур и пять рыцарей Б, В, Г, Д и Е сидели за круглым столом (см. рисунок) и обсуждали битву с драконом.Б сказал: «Дракона победил я». В сказал: «Дракона одолел Артур». Г сказал: «Это не Артур его победил». Д сказал: «Дракона одолел рыцарь Б». Е сказал: «Артур победил дракона». Известно, что Артур и один какой-то рыцарь всегда говорят правду и сидят рядом. Ровно два рыцаря всегда лгут и не сидят рядом. Оставшиеся два рыцаря могут как лгать, так и говорить правду, и тоже не сидят рядом. Кто победил дракона, если это сделал только один из шести, сидящих за столом? Время работы 1 час 30 минут |